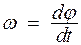 .
.
9. Угловое ускорение:
 .
.
10. Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:


 ,
,
где  - линейная скорость:
- линейная скорость:  и
и  - тангенциальное и нормальное ускорения,
- тангенциальное и нормальное ускорения,  - угловая скорость,
- угловая скорость,  - угловое ускорение,
- угловое ускорение,  - радиус окружности.
- радиус окружности.
11. Полное ускорение:
 .
.
12. Угол между полным ускорением 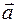 и нормальным ускорением
и нормальным ускорением  :
:
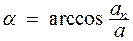 .
.
13. Уравнение гармонических колебаний материальной точки:
 ,
,
где 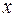 - смещение, А - амплитуда колебаний,
- смещение, А - амплитуда колебаний,  - угловая или циклическая частота,
- угловая или циклическая частота,  - начальная фаза.
- начальная фаза.
14. Скорость материальной точки, совершающей гармонические колебания:
 .
.
15. Ускорение материальной точки, совершающей гармонические колебания:
 .
.
16. Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания:
 .
.
б) начальная фаза результирующего колебания
 .
.
17. Уравнения, описывающие траекторию точки, участвующей в двух взаимно перпендикулярных колебаниях:
 .
.
a)  , (если разность фаз
, (если разность фаз  ),
),
б)  , (если разность фаз
, (если разность фаз  ),
),
в)  , (если разность фаз
, (если разность фаз  ).
).
18. Уравнение плоской бегущей волны:
 ,
,
где y – смещение любой из точек среды с координатой 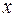 в момент
в момент 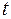 ,
,  - скорость распространения колебания в среде.
- скорость распространения колебания в среде.
19. Связь разности фаз колебаний  с расстоянием между точками среды
с расстоянием между точками среды  , отсчитанными в направлении распространения колебаний
, отсчитанными в направлении распространения колебаний  ,
,
где  - длина волны.
- длина волны.
20. Импульс материальной точки с массой m, движущейся поступательно со скоростью  :
:
 .
.
21. Второй закон Ньютона:  ,
,
где  - сила, действующая на тело.
- сила, действующая на тело.
22. Силы, рассматриваемые в механике:
а) сила упругости:  ,
,
где 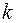 - коэффициент упругости (в случае пружины - жесткость),
- коэффициент упругости (в случае пружины - жесткость), 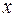 - абсолютная деформация,
- абсолютная деформация,
б) сила тяжести  .
.
в) сила гравитационного взаимодействия  ,
,
где  - гравитационная постоянная,
- гравитационная постоянная,  и
и  - массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля:
- массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля:
 .
.
г) сила трения (скольжения)  ,
,
где m - коэффициент трения, N - сила нормального давления.
23. Закон сохранения импульса:
 ,
,
или для двух тел (i = 2),
 ,
,
где  и
и  - скорости тел в момент времени, принятый за начальный,
- скорости тел в момент времени, принятый за начальный, 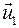 и
и 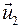 - скорости тех же тел в момент времени, принятый за конечный.
- скорости тех же тел в момент времени, принятый за конечный.
24. Кинетическая энергия тела, движущегося поступательно:
 или
или  .
.
25. Потенциальная энергия:
а) упругодеформированной пружины:
 ,
,
где 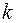 - жесткость пружины,
- жесткость пружины, 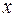 - абсолютная деформация.
- абсолютная деформация.
б) гравитационного взаимодействия:
 ,
,
где  - гравитационная постоянная,
- гравитационная постоянная,  и
и 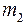 - массы взаимодействующих тел, r - расстояние между ними (тела рассматриваются как материальные точки),
- массы взаимодействующих тел, r - расстояние между ними (тела рассматриваются как материальные точки),
в) тела, находящегося в однородном поле силы тяжести:
 ,
,
где  - ускорение свободного падения,
- ускорение свободного падения,  - высота тела над уровнем, принятым за нулевой (формула справедлива при условии
- высота тела над уровнем, принятым за нулевой (формула справедлива при условии  , где
, где  - радиус Земли)
- радиус Земли)
26. Закон сохранения механической энергии:
.
27. Работа  , совершаемая внешними силами, определяется как мера изменения энергии системы:
, совершаемая внешними силами, определяется как мера изменения энергии системы:
 .
.
28. Основное уравнение динамики вращательного движения относительно неподвижной оси:
 ,
,
где  - результирующий момент внешних сил, действующих на тело,
- результирующий момент внешних сил, действующих на тело,  - угловое ускорение,
- угловое ускорение,  - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.
29. Момент инерции некоторых тел массой m относительно оси, проходящей через центр масс:
а) стержня длины  относительно оси, перпендикулярной стержню,
относительно оси, перпендикулярной стержню,
 .
.
б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),
 ,
,
где  - радиус обруча (цилиндра),
- радиус обруча (цилиндра),
в) диска радиусом R относительно оси, перпендикулярной плоскости диска,
 .
.
30. Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:
 ,
,
где  и
и  - момент инерции системы тел и угловая скорость вращения в момент времени, принятый за начальный,
- момент инерции системы тел и угловая скорость вращения в момент времени, принятый за начальный,  и
и  - момент инерции и угловая скорость в момент времени, принятый за конечный.
- момент инерции и угловая скорость в момент времени, принятый за конечный.
31. Момент импульса тела, вращающегося относительно неподвижной оси:
 ,
,
где  - угловая скорость тела.
- угловая скорость тела.
32. Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
 или
или  .
.
1.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид: 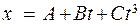 , где A = 2 м, B = 1 м/с, C = 0, 5 м/с3. Найти координату
, где A = 2 м, B = 1 м/с, C = 0, 5 м/с3. Найти координату 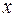 , скорость
, скорость  и ускорение
и ускорение  точки в момент времени t = 2 c.
точки в момент времени t = 2 c.
Решение: Координату 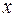 найдем, подставив в уравнение движения числовые значения коэффициентов A, B, C и времени t:
найдем, подставив в уравнение движения числовые значения коэффициентов A, B, C и времени t:
 .
.
Мгновенная скорость есть первая производная от координаты по времени:

в момент времени t = 2 c.

Ускорение точки найдем, взяв первую производную от скорости по времени:
 .
.
В момент времени t = 2 c.
 .
.
Пример 2. Тело вращается вокруг неподвижной оси по закону  , где
, где  ,
,  ,
,  . Найти полное ускорение точки, находящейся на расстоянии r = 0, 1 м от оси вращения, для момента времени t = 4 c.
. Найти полное ускорение точки, находящейся на расстоянии r = 0, 1 м от оси вращения, для момента времени t = 4 c.
Решение: Полное ускорение
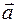
тела, движущегося по криволинейной
траектории, может быть найдено как геометрическая сумма тангенциального ускорения  , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения  , направленного к центру кривизны траектории (Рис. 1):
, направленного к центру кривизны траектории (Рис. 1):

Так как векторы  и
и  взаимно перпендикулярны, то абсолютное значение ускорения
взаимно перпендикулярны, то абсолютное значение ускорения
 (1)
(1)
Тангенциальное и нормальное ускорение точки вращающегося тела выражается формулой:

где  - угловая скорость тела,
- угловая скорость тела,  - угловое ускорение. Подставляя найденные выражения для
- угловое ускорение. Подставляя найденные выражения для  в формулу (1), находим
в формулу (1), находим
 (2)
(2)
Угловую скорость найдем, взяв производную от угла поворота по времени:

В момент времени t = 4 c угловая скорость  = (20+2(-2)4) = 4 рад/с.
= (20+2(-2)4) = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:

Это выражение не содержит времени, следовательно, угловое ускорение данного движения постоянно. Подставляя найденные значения  и
и  , и заданное значение
, и заданное значение 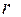 в формулу (2) получим
в формулу (2) получим

Пример 3. Шар массой  , движущийся горизонтально с некоторой скоростью
, движущийся горизонтально с некоторой скоростью 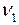 , столкнулся cнеподвижным шаром массой
, столкнулся cнеподвижным шаром массой 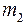 . Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму?
. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму?
Решение: Доля энергии, переданной первым шаром второму, выразится отношением:
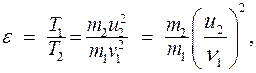 (1)
(1)
где  – кинетическая энергия первого шара до удара,
– кинетическая энергия первого шара до удара,  ,
,  - скорость и кинетическая энергия второго шара после удара.
- скорость и кинетическая энергия второго шара после удара.
Как видноиз формулы (3), для определения  надо найти
надо найти  . При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закон сохранения импульса и закон сохранения механической энергии. Пользуясь этими законами, найдем
. При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закон сохранения импульса и закон сохранения механической энергии. Пользуясь этими законами, найдем  . По закону сохранения импульса, учитывая, что второй шар до удара покоился, получим.
. По закону сохранения импульса, учитывая, что второй шар до удара покоился, получим.
 (2)
(2)
позакону механической энергии
 (3)
(3)
решая совместно уравнения (2) и (3), найдем
 (4)
(4)
Подставимвыражение (4) в формулу (1) и, сократив на 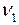 , получим
, получим
 .
.
Из полученного соотношения видно, что доля переданной энергии не изменится, если шары поменяются местами.
Пример 4. Через блок в виде сплошного диска, имеющего массу  = 80 г. (Рис. 2) перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами
= 80 г. (Рис. 2) перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами  = 100 г и
= 100 г и 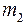 = 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением нити пренебречь.
= 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением нити пренебречь.


Рис. 2
Решение: Воспользуемся основными уравнениями динамики поступательного и вращательного движения. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: силы тяжести  и сила упругости (сила натяжения нити)
и сила упругости (сила натяжения нити)  . Спроектируем эти силы на ось
. Спроектируем эти силы на ось 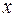 , которую направим вертикально вниз и напишем уравнение движения (второй закон Ньютона) в координатной форме:
, которую направим вертикально вниз и напишем уравнение движения (второй закон Ньютона) в координатной форме:
 (1)
(1)
Уравнение движения для второго груза запишется аналогично:
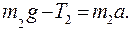 (2)
(2)
Под действием двух моментов сил  и
и  относительно оси
относительно оси  , перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение  . Согласно основному уравнению динамики вращательного движения
. Согласно основному уравнению динамики вращательного движения
 (3)
(3)
где  момент инерции блока (сплошного диска) относительно оси z. Согласно третьему закону Ньютона, силы
момент инерции блока (сплошного диска) относительно оси z. Согласно третьему закону Ньютона, силы  и
и 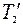 по абсолютному значению равны силам
по абсолютному значению равны силам  и
и  .Воспользовавшись этим, поставим в уравнение (3) вместо
.Воспользовавшись этим, поставим в уравнение (3) вместо  и
и  выражения для
выражения для  и
и  , получив их предварительно из уравнений (1) и (2):
, получив их предварительно из уравнений (1) и (2):

После сокращения на  и перегруппировки найденных членов найдем интересующее нас ускорение.
и перегруппировки найденных членов найдем интересующее нас ускорение.
 (4)
(4)
Отношение масс в правой части формулы (4) есть величина безразмерная.
Поэтому массы  и
и 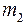 можно выразить в граммах, так, как они даны в условии задачи. Ускорение надо выразить в единицах СИ. После подстановки получим:
можно выразить в граммах, так, как они даны в условии задачи. Ускорение надо выразить в единицах СИ. После подстановки получим:

Пример 5. Маховик в виде сплошного диска радиусом  = 0, 2 м и массой
= 0, 2 м и массой  = 50 кг раскручен до частоты вращения
= 50 кг раскручен до частоты вращения  = 480 мин-1 и предоставлен самому себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент
= 480 мин-1 и предоставлен самому себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент  сил трения.
сил трения.
Решение: Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде:
 (1)
(1)
где  - изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика, за интервал времени
- изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика, за интервал времени  ,
,  - момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси. Момент сил трения можно считать не изменяющимся с течением времени (
- момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси. Момент сил трения можно считать не изменяющимся с течением времени ( ), поэтому интегрирование уравнения (1) приводит к выражению
), поэтому интегрирование уравнения (1) приводит к выражению
 (2)
(2)
При вращении твердого тела относительно неподвижной оси изменение момента импульса:
 (3)
(3)
где  - момент инерции маховика относительно оси z,
- момент инерции маховика относительно оси z,  - изменение угловой скорости маховика. Приравняв правые части равенства (2) и (3), получим
- изменение угловой скорости маховика. Приравняв правые части равенства (2) и (3), получим
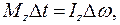
откуда
 (4)
(4)
Момент инерциимаховика в виде сплошного диска определяется по формуле
 (5)
(5)
Изменение угловой скорости  выразим через конечную
выразим через конечную  и начальную
и начальную  частоты вращения, пользуясьсоотношением
частоты вращения, пользуясьсоотношением  . Подставив в формулу(4)найденное выражение
. Подставив в формулу(4)найденное выражение  и
и  , получим
, получим
 (5)
(5)
Проверим, совпадают ли размерности правой и левой частей равенства (5). Размерность левой части:

Размерность правой части:

что совпадает с размерностью левой части. Выпишем величины, входящие в формулу (5) и произведем вычисления:  = 50 кг,
= 50 кг,  = 0, 2 м,
= 0, 2 м, 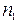 = 480 мин,
= 480 мин,  = 0, Dt = 50 с
= 0, Dt = 50 с

Знак минус показывает, что силы трения оказывают на маховик тормозящее действие.
Пример 6. Точка совершает гармонические колебания с частотой 10 Гц. В момент времени, принятый за начальный, точка имела максимальное смещение  = 1 мм. Написать уравнение колебаний точки и начертить график.
= 1 мм. Написать уравнение колебаний точки и начертить график.
Решение: Уравнение колебаний точки можно записать в виде
 (1)
(1)
или
 (2)
(2)
где  - амплитуда колебаний,
- амплитуда колебаний,  - циклическая частота,
- циклическая частота, 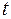 - время,
- время,  и
и  - начальные фазы, соответствующие форме записи (1) и (2). По определению, амплитуда колебаний
- начальные фазы, соответствующие форме записи (1) и (2). По определению, амплитуда колебаний
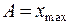 . (3)
. (3)
Циклическая частота связана с частотой  соотношением
соотношением
 . (4)
. (4)
Начальная фаза колебаний зависит от формы записи. Если использовать формулу (1), то начальную фазу можно определить из условия в момент t = 0:

откуда
 ,
,
или
 (5)
(5)
Изменение фазы на  не изменяет состояния колебательного движения, поэтому можно принять
не изменяет состояния колебательного движения, поэтому можно принять
 (6)
(6)
В случае второй формы записи получаем

или 
По тем же соображениям, что и в первом случае, находим
 (7)
(7)
С учетом равенства (3) - (6) уравнения колебаний будут иметь вид:

где x max = 1 мм = 10-3 м , v = 10 Гц.
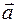 тела, движущегося по криволинейной
тела, движущегося по криволинейной

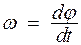 .
. .
.

 ,
, - линейная скорость:
- линейная скорость:  и
и  - тангенциальное и нормальное ускорения,
- тангенциальное и нормальное ускорения,  - угловая скорость,
- угловая скорость,  - угловое ускорение,
- угловое ускорение,  - радиус окружности.
- радиус окружности. .
. :
: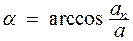 .
. ,
,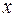 - смещение, А - амплитуда колебаний,
- смещение, А - амплитуда колебаний,  - начальная фаза.
- начальная фаза. .
. .
. .
. .
. .
. , (если разность фаз
, (если разность фаз  ),
), , (если разность фаз
, (если разность фаз  ),
), , (если разность фаз
, (если разность фаз  ).
). ,
,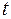 ,
,  с расстоянием между точками среды
с расстоянием между точками среды  , отсчитанными в направлении распространения колебаний
, отсчитанными в направлении распространения колебаний  ,
, - длина волны.
- длина волны. :
: .
. ,
, - сила, действующая на тело.
- сила, действующая на тело. ,
,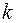 - коэффициент упругости (в случае пружины - жесткость),
- коэффициент упругости (в случае пружины - жесткость),  .
. ,
, - гравитационная постоянная,
- гравитационная постоянная,  и
и  - массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля:
- массы взаимодействующих тел, r - расстояние между телами (тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряженность G гравитационного поля: .
. ,
, ,
, ,
, и
и  - скорости тел в момент времени, принятый за начальный,
- скорости тел в момент времени, принятый за начальный, 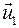 и
и 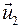 - скорости тех же тел в момент времени, принятый за конечный.
- скорости тех же тел в момент времени, принятый за конечный. или
или  .
. ,
, ,
, - гравитационная постоянная,
- гравитационная постоянная, 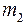 - массы взаимодействующих тел, r - расстояние между ними (тела рассматриваются как материальные точки),
- массы взаимодействующих тел, r - расстояние между ними (тела рассматриваются как материальные точки), ,
, - ускорение свободного падения,
- ускорение свободного падения,  - высота тела над уровнем, принятым за нулевой (формула справедлива при условии
- высота тела над уровнем, принятым за нулевой (формула справедлива при условии  , где
, где  , совершаемая внешними силами, определяется как мера изменения энергии системы:
, совершаемая внешними силами, определяется как мера изменения энергии системы: .
. ,
, - результирующий момент внешних сил, действующих на тело,
- результирующий момент внешних сил, действующих на тело,  - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения. относительно оси, перпендикулярной стержню,
относительно оси, перпендикулярной стержню, .
. ,
, .
. ,
, и
и  - момент инерции системы тел и угловая скорость вращения в момент времени, принятый за начальный,
- момент инерции системы тел и угловая скорость вращения в момент времени, принятый за начальный,  и
и  - момент инерции и угловая скорость в момент времени, принятый за конечный.
- момент инерции и угловая скорость в момент времени, принятый за конечный. ,
, или
или  .
.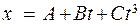 , где A = 2 м, B = 1 м/с, C = 0, 5 м/с3. Найти координату
, где A = 2 м, B = 1 м/с, C = 0, 5 м/с3. Найти координату  точки в момент времени t = 2 c.
точки в момент времени t = 2 c. .
.

 .
. .
. , где
, где  ,
,  ,
,  . Найти полное ускорение точки, находящейся на расстоянии r = 0, 1 м от оси вращения, для момента времени t = 4 c.
. Найти полное ускорение точки, находящейся на расстоянии r = 0, 1 м от оси вращения, для момента времени t = 4 c.

 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения  , направленного к центру кривизны траектории (Рис. 1):
, направленного к центру кривизны траектории (Рис. 1):
 и
и  (1)
(1)
 в формулу (1), находим
в формулу (1), находим (2)
(2)

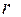 в формулу (2) получим
в формулу (2) получим
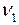 , столкнулся cнеподвижным шаром массой
, столкнулся cнеподвижным шаром массой 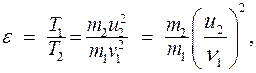 (1)
(1) – кинетическая энергия первого шара до удара,
– кинетическая энергия первого шара до удара,  ,
,  - скорость и кинетическая энергия второго шара после удара.
- скорость и кинетическая энергия второго шара после удара. надо найти
надо найти  (2)
(2) (3)
(3) (4)
(4) .
. = 80 г. (Рис. 2) перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами
= 80 г. (Рис. 2) перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами 

 и сила упругости (сила натяжения нити)
и сила упругости (сила натяжения нити)  . Спроектируем эти силы на ось
. Спроектируем эти силы на ось  (1)
(1)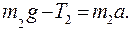 (2)
(2) и
и  относительно оси
относительно оси  , перпендикулярной плоскости чертежа, блок приобретает угловое ускорение
, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение  . Согласно основному уравнению динамики вращательного движения
. Согласно основному уравнению динамики вращательного движения (3)
(3) момент инерции блока (сплошного диска) относительно оси z. Согласно третьему закону Ньютона, силы
момент инерции блока (сплошного диска) относительно оси z. Согласно третьему закону Ньютона, силы  и
и 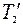 по абсолютному значению равны силам
по абсолютному значению равны силам  и
и  и
и  выражения для
выражения для 
 и перегруппировки найденных членов найдем интересующее нас ускорение.
и перегруппировки найденных членов найдем интересующее нас ускорение. (4)
(4)
 = 480 мин-1 и предоставлен самому себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент
= 480 мин-1 и предоставлен самому себе. Под действием силы трения маховик остановился через t = 50 с. Найти момент  (1)
(1) - изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика, за интервал времени
- изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика, за интервал времени  ,
,  - момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси. Момент сил трения можно считать не изменяющимся с течением времени (
- момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси. Момент сил трения можно считать не изменяющимся с течением времени ( ), поэтому интегрирование уравнения (1) приводит к выражению
), поэтому интегрирование уравнения (1) приводит к выражению (2)
(2) (3)
(3) - момент инерции маховика относительно оси z,
- момент инерции маховика относительно оси z,  - изменение угловой скорости маховика. Приравняв правые части равенства (2) и (3), получим
- изменение угловой скорости маховика. Приравняв правые части равенства (2) и (3), получим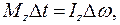
 (4)
(4) (5)
(5) выразим через конечную
выразим через конечную  и начальную
и начальную  . Подставив в формулу(4)найденное выражение
. Подставив в формулу(4)найденное выражение  и
и  , получим
, получим (5)
(5)

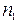 = 480 мин,
= 480 мин,  = 0, Dt = 50 с
= 0, Dt = 50 с
 = 1 мм. Написать уравнение колебаний точки и начертить график.
= 1 мм. Написать уравнение колебаний точки и начертить график. (1)
(1) (2)
(2) и
и  - начальные фазы, соответствующие форме записи (1) и (2). По определению, амплитуда колебаний
- начальные фазы, соответствующие форме записи (1) и (2). По определению, амплитуда колебаний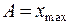 . (3)
. (3) . (4)
. (4)
 ,
, (5)
(5) не изменяет состояния колебательного движения, поэтому можно принять
не изменяет состояния колебательного движения, поэтому можно принять (6)
(6)

 (7)
(7)




