Формирование ДБП. Балансный смеситель
Как было сказано, ДБП является результатом перемножения модулирующего сигнала и колебания несущей частоты (3.1). Эту операцию выполняют схемы, называемые балансными смесителями модуляторами (БМ), реализуемые в виде ИС (рис 3.4). Схема состоит из четырех дифференциальных усилителей (ДУ). Усилитель входного модулирующего (управляющего) сигнала, который служит для развязки выхода формирователя модулирующего сигнала и собственно БМ, выполнен на полевых транзисторах VT1 и VT2. Со стоков транзисторов VT1 и VT2 снимают два симметричных противофазных модулирующих напряжения:
Рис. 3.4. Схема балансного модулятора Отметим что транзисторы ДУ VT7 – VT8, как и ДУ VT1, VT2, работают в линейном режиме усиления. Транзисторы БМ VT3 – VT4 и VT5 – VT6 работают в нелинейном режиме, так как модуляция – процесс нелинейный. Представим характеристики этих транзисторов экспоненциальной функцией
В отсутствие модулирующего сигнала ток каждого транзистора
Модулирующее напряжение
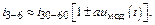 (3.7) (3.7)
С учетом этих соображений токи транзисторов БМ можно записать так:
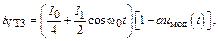

Выходные токи (за вычетом постоянной составляющей, которую не пропускают разделительные конденсаторы):
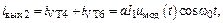 (3.8') (3.8')
представляют собой произведение модулирующего сигнала и колебания несущей. Они одинаковы по величине и противоположны по фазе. Токи модулирующих частот и несущей частоты на выходах скомпенсированы. Заметим, что в разложении (3.7) ограничились только линейным членом. Из-за составляющих с более высокими степенями возникают комбинационные частоты высших порядков, для задержки которых на выходе БМ ставят полосовой фильтр, пропускающий только комбинационные 1-го порядка (т.е. ДБП сигнал) в рабочем диапазоне несущих частот. 3.3. Нелинейные искажения При усилении сигналов с линейной модуляцией необходимо сохранять их форму, что при изменении амплитуды сигнала (рис. 3.3) требует линейного усиления. Нелинейности транзисторов вызывают искажения сигналов, что приводит к появлению в спектре сигнала новых составляющих: комбинационных частот высших порядков. Рассмотрим вначале искажения, вызванные нелинейностью статических характеристик транзисторов. Анализ будем производить традиционным методом с использованием двухчастотного испытательного сигнала. Представим сигнал (3.3) в несколько другой записи:
 (3.9) (3.9)
где
Две комбинационные 1-го порядка колебательного сигнала f 1 и f 2 показаны на рис. 3.5.
Рис. 3.5. Спектр ДБП при нелинейных искажениях Статическую характеристику транзистора (рис. 3.6) запишем в виде степенного ряда:
Рис. 3.6. Характеристика транзистора Проанализируем отдельные составляющие степенного ряда (3.10). Линейный член Квадратичный член Кубический член Эти составляющие, как следует из выражения
 (3.11) (3.11)
Продолжая исследования далее, получим, что только нечетные степени разложения (3.10) создают комбинационные частоты, находящиеся в полосе сигнала: 3 f 1–2 f 2, 3 f 2–2 f 1, 4 f 1–3 f 2, 4 f 2–3 f 1 и т.д. Именно эти комбинационные составляющие и определяют уровень нелинейных искажений усиливаемого сигнала. Ограничиваясь только комбинационными составляющими 3-го порядка, получим для коэффициента нелинейных искажений
Для обеспечения линейности усиления сигналов с меняющейся амплитудой надо либо работать на линейном участке характеристики транзистора (в режиме А), либо с углом отсечки тока q = 90°. На практике это соответствует выбору такого смещения E см, когда коэффициенты a 3 и a 5 в разложении (3.10) минимальны. Второй причиной возникновения нелинейных искажений является амплитудно-фазовая конверсия (АФК), т. е. изменение фазы выходного сигнала из-за изменения его амплитуды. Входной сигнал (3.9′)
 (3.13) (3.13)
где При анализе амплитудно-фазовой конверсии пренебрежем искажениями, вызванными нелинейностью статических характеристик транзистора, так как они, как и всякие искажения, малы, поэтому взаимным влиянием различных факторов можно пренебречь. Фазоамплитудная характеристика УМ приведена на рис. 3.7.
Рис. 3.7. Зависимость фазового сдвига Представим ее в виде степенного ряда:
Теперь запишем выражение для амплитуды (огибающей) сигнала. Амплитуда – положительная величина, так что из (3.9′) следует
 (3.15) (3.15)
Функция
Ограничим ряд в (3.14) линейным членом, подставим в него (3.15) и (3.16) и полученный результат далее в (3.13), тогда
Рис. 3.8. Функция Сдвиг j1 мал (искажения малы!), поэтому

Из анализа второго слагаемого (3.18) следует, что в спектре появятся комбинационные составляющие f 0 ± 3Ω (2 f 2 – f 1, 2 f 1 – f 2), f 0 ± 5Ω (3 f 2 – 2 f 1,
|

 и
и  , которые подают на сдвоенный ДУ на транзисторах VT3 – VT4 и VT5 – VT6. Ток, подводимый к этим транзисторам, содержит постоянную составляющую
, которые подают на сдвоенный ДУ на транзисторах VT3 – VT4 и VT5 – VT6. Ток, подводимый к этим транзисторам, содержит постоянную составляющую  и радиочастотную составляющую
и радиочастотную составляющую  так как на базы транзисторов ДУ VT7 и VT8 подано противофазное напряжение радиочастоты (несущей). При этом через транзисторы VT3 и VT4 проходит ток
так как на базы транзисторов ДУ VT7 и VT8 подано противофазное напряжение радиочастоты (несущей). При этом через транзисторы VT3 и VT4 проходит ток  , а через транзисторы VT5 и VT6 ток
, а через транзисторы VT5 и VT6 ток 

 (3.6)
(3.6)
 (3.6')
(3.6') мало, и, используя разложение в ряд Тейлора, получим
мало, и, используя разложение в ряд Тейлора, получим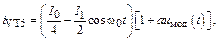

 (3.8)
(3.8) ,
,  ,
,  – частота несущей, а
– частота несущей, а  – частота огибающей, так что (3.9) можно записать в виде
– частота огибающей, так что (3.9) можно записать в виде (3.9')
(3.9')
 (3.10)
(3.10)
 обеспечивает линейное усиление комбинационных частот первого порядка f 1 и f 2.Амплитуда выходного тока
обеспечивает линейное усиление комбинационных частот первого порядка f 1 и f 2.Амплитуда выходного тока 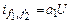 .
. генерирует следующие спектральные соcтавляющие: f 1, f 2 – изменяющие (обычно незначительно) коэффициент усиления испытательного сигнала;
генерирует следующие спектральные соcтавляющие: f 1, f 2 – изменяющие (обычно незначительно) коэффициент усиления испытательного сигнала;  , 2 f 1,
, 2 f 1,  – комбинационные
– комбинационные  создает ток частот: f 1, f 2, несколько влияющих на коэффициент усиления испытательного сигнала;
создает ток частот: f 1, f 2, несколько влияющих на коэффициент усиления испытательного сигнала;  ,
,  ,
,  , 2 f 1, 2 f 2, 3 f 1, 3 f 2, f 2 – f 1 – комбинационные 2-го и 3-го порядков, фильтруемые выходной колебательной системой;
, 2 f 1, 2 f 2, 3 f 1, 3 f 2, f 2 – f 1 – комбинационные 2-го и 3-го порядков, фильтруемые выходной колебательной системой;  ,
,  – комбинационные 3-го порядка, находящиеся в полосе сигнала, колебательная система их отфильтровать не может (рис. 3.5).
– комбинационные 3-го порядка, находящиеся в полосе сигнала, колебательная система их отфильтровать не может (рис. 3.5). , равны:
, равны: (3.11')
(3.11') (3.12)
(3.12) – фазовый сдвиг в усилителе мощности.
– фазовый сдвиг в усилителе мощности.
 (3.14)
(3.14) (рис. 3.8) при разложении в ряд Фурье содержит только четные гармоники Ω t:
(рис. 3.8) при разложении в ряд Фурье содержит только четные гармоники Ω t: (3.16)
(3.16) где
где  – постоянный фазовый сдвиг.
– постоянный фазовый сдвиг.

 (3.18)
(3.18)


