Частотная модуляция. Спектр сигнала
До 1991 г., когда появились цифровые стандарты телефонии, частотная модуляция была универсальным методом передачи в любых сетях подвижной связи. Сейчас сети аналоговой сотовой связи практически исчезли, но продолжают работать транкинговые сети с ЧМ. При ЧМ частота радиосигнала меняется прямо пропорционально мгновенному значению модулирующего напряжения [3], т.е. Соответственно, колебания радиочастоты
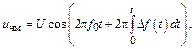 (3.19) (3.19)
где f 0 – центральная частота радиосигнала. Максимальное отклонение частоты Δ f max(t) называют девиацией частоты. Речевые сигналы многочастотны. Более того, речь содержит наряду с отдельными дискретными составляющими шум, так что спектр речи сплошной. Поэтому Тогда (3.19) можно преобразовать к виду
 (3.20) (3.20)
где Иначе
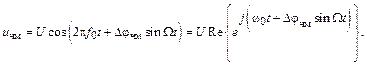 (3.21) (3.21)
Для проведения спектрального анализа ЧМ колебаний введем производящую функции Бесселя 1-го рода
 (3.22) (3.22)
где Подставляя (3.22) в (3.21), получаем
(3.23) Таким образом, при модуляции гармоническим напряжением ЧМ сигнал имеет бесконечный линейчатый спектр (рис. 3.9), где амплитуды всех составляющих определяют функции Бесселя.
Рис. 3.9. Спектр ЧМ сигнала Графики функций
Рис. 3.10. Графики функций Бесселя Как следует из рис 3.10, амплитуда частоты f 0 меняет знак, а при
Рис. 3.11. Спектр ЧМ сигнала при малых индексах Высокая помехозащищенность ЧМ сигналов достигается при Теоретически полоса ЧМ сигнала бесконечна. Фактически сигнал ограничен полосой, включающей спектральные составляющие, содержащие не менее 90% полной мощности сигнала. На практике полосу ЧМ сигнала часто определяют так [3]:
 (3.24) (3.24)
Теоретически ЧМ сигнал имеет постоянную амплитуду, однако из-за ограничения полосы возникает небольшая паразитная амплитудная модуляция. Поэтому при приеме ЧМ сигнал подвергают амплитудному ограничению, а при передаче в усилителях мощности используют слабоперенапряженные режимы работы транзисторов.
|

 .
. – полигармонический сигнал. Для упрощения анализа ЧМ радиосигнала будем использовать моногармоническое модулирующее испытательное напряжение
– полигармонический сигнал. Для упрощения анализа ЧМ радиосигнала будем использовать моногармоническое модулирующее испытательное напряжение  где Ω =2π F.
где Ω =2π F. = kA – девиация частоты,
= kA – девиация частоты, 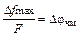 – индекс частотной модуляции.
– индекс частотной модуляции.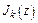 – функция Бесселя 1-го рода k -го порядка.
– функция Бесселя 1-го рода k -го порядка.

 …
…  представлены на рис. 3.10.
представлены на рис. 3.10.
 и ряде последующих значений обращается в нуль. Максимумы функций
и ряде последующих значений обращается в нуль. Максимумы функций  расположены вблизи z = n. Чем больше
расположены вблизи z = n. Чем больше  , тем большее число составляющих будет значимым в спектре. Если
, тем большее число составляющих будет значимым в спектре. Если  , то спектр состоит из трех составляющих (рис. 3.11).
, то спектр состоит из трех составляющих (рис. 3.11).
 . Поэтому в случае речевого модулирующего сигнала с полосой 300…3400 Гц, предварительно до модуляции вводят предкоррекцию сигнала, поднимая уровень его высокочастотных составляющих.
. Поэтому в случае речевого модулирующего сигнала с полосой 300…3400 Гц, предварительно до модуляции вводят предкоррекцию сигнала, поднимая уровень его высокочастотных составляющих.


