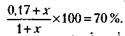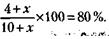РЕШЕНИЯ 6 страница
Нетрудно сообразить, что для успеха сделки ваш первоначальный вклад должен быть больше, чем та сумма, которую вы должны ежемесячно выплачивать банку. Математически это условие запишется так. Обозначим необходимую для второй сделки сумму первоначального вклада через х. Тогда х х 2 - 2400 > х, откуда видно, что х > 2400 руб.
182. 1) На 50%. 2) На 100%.
183. Извлечение корня квадратного из обеих частей выражения (**) допускает два решения. Первое решение (***) неверно. Верно второе решение: x-z = -(y-z), из которого следует, что х- 2 = z- у, а это не приводит к ошибке. Действительно, так как z и у положительны, то из равенства (*) следует, что
Но это означает, что в случае 1) х - у > 0, у - z < 0 и равенство (***) неверно, или в случае 2) х - z < 0 х - у > 0 и равенство (***) также неверно. Второе же решение не противоречит ни одному из этих случаев.
184. Обозначая цену товара до и после снижения через х1 и х2, получим следующее очевидное соотношение:
из которого видно, что х1 = 100 руб.
185. Примем первоначальную цену товара и зарплату в 1000 руб. Тогда новая цена товара будет 150 000 руб., а новая зарплата – 100 000. Реальная зарплата при этом уменьшилась на
186. Вначале рассчитывается, каков процент неучастия объединения во внешнеэкономических операциях со всеми странами, кроме США: с Великобританией это 20 % (100 % - 80 %), с Японией – 15 %, с Германией – 10 %. Затем находится суммарный процент в операциях со всеми этими странами, который равен 20 % + 15 % + 10 % = 45 %. Этот процент следует вычесть из процента участия в операциях США, что и будет ответом по данной задаче: 60 % - 45 % = 15 %.
187. Надо разделить 25 руб. на 50 частей (49 + 1). Это даст 25: 50 = 0, 5 руб., что явится меньшей из двух частей. Большая часть будет содержать 49 частей и составит 0, 5 х 49 = 24, 5 руб.
188. По формуле теории вероятностей необходимое количество операций (N) будет равно:
189. По формулам, приведенным в решении задачи 171: 1) Д = 100+ 50 =150 млн руб. 2) ОПР = 150 - 90 = 60 млн руб. 3) НПР = 35 % от ОПР = 21 млн руб. 4) ЧПР = 60-21 = 39 млн руб. 5) Взносы в бюджет из фонда оплаты труда (ВОТ): ВОТ = 39 % от 50 млн руб. = 19, 5 млн руб.
190. 1) 100 % + 20 % (это выручка + НДС) = 240 млн руб. Откуда НДС = 40 млн руб. 2) Предприятие уплатит НДС по формуле:
Следовательно, 16, 67 % от (300 - 240) млн руб. = 10 млн руб.
191. Средняя месячная оплата труда менеджера составляет:
За 7 месяцев зарплата в деньгах составит: 52 тыс. у. д. ед. х 7 мес. = 364 тыс. у. д. ед. Но за это время менеджер уже получил 240 тыс. у. д. ед. Следовательно, премия оценена в 364 - 240= 124 тыс.у.д.ед.
192. Выход существует. Ведь условия соглашения касаются лишь выигрыша первого дела. Значит, если учитель подаст в суд повторно, то оговоренное условие уже не будет действовать, и он сможет получить деньги по решению суда.
193. Для быстрого устного решения задачи нужно сообразить, что сумма последовательных чисел от 1 до 100 складывается из следующей суммы пар чисел: 1-го с последним, 2-го с предпоследним и т. д. Каждая такая пара равна в сумме 101, а всего таких пар 50. Итак, нужно просто у множить 101 на 50, что легко сделать устно: 101 х 50 = 5050. 194. 80 % от 25 % равно 20 %.
196. 12 павильонов (включая два административных). Решение задачи ясно из рисунка.
197. Эту задачу удобно начинать решать с конца. Обозначим через х конечные капиталы каждого из партнеров. Тогда к началу третьей операции (в этом месяце) текущие капиталы партнеров А, Б, В должны были соответственно составить К началу второй операции (месяц назад) текущие капиталы партнеров А, Б, В соответственно составляли А к началу первой операции (два месяца назад) начальные капиталы партнеров А, Б, В выглядели так:
При этом потери партнера А равны:
Следовательно, начальный капитал партнера А равен:
партнера Б
партнера В:
198. Обозначим через х и у вложения в операции А и Б соответственно. Тогда условие задачи можно записать так:
Решим систему из двух уравнений с двумя неизвестными. Из (1) следует: у = 8 - х. Подставляя значение у в(2), получим:
откуда
Решая квадратное уравнение по стандартной формуле, получим:
х1 = 6 (х2 не подходит, так как при нем х < у, что противоречит условию). Следовательно, сумма вложения в операцию А равна 6 млн у. д. ед., в операцию Б: 8 – 6 = 2 млн у. д. ед. 199. Обозначим через х возраст сооружения Б. Тогда условие задачи можно записать так:
Следовательно: возраст сооружения А – 9 лет, возраст сооружения Б – 3 года, возраст сооружения В – 45 лет, возраст сооружения Г – 3 года, возраст сооружения Д – 70 лет. 200. Обозначим через х количество дней, когда предприниматель был здоров, а через у – нездоров. Тогда условие задачи можно записать так:
Здесь х и у – целые положительные числа. Произведем перебор х. При х = 1 выражение (*) будет таким:
откуда
(такое дробное значение у не подходит). При х = 2 выражение (*) будет таким:
откуда
(это значение у подходит). Итак: 1) Количество дней, когда предприниматель был здоров, равно 2, нездоров – 8. 2) Действие договора продолжалось 2 + 8 = 10 дней. 201. Интерполируя с помощью таблицы сложных процентов, получим:
Откуда х1 = 12 месяцев.
202. Интерполируя с помощью таблицы сложных процентов, получим:
откуда х = 4 дня. 203. Прибыль торговой фирмы может составить для каждой партии товара: при закупке партий в 1000 единиц (100 - 80) х 1000 = 20 000 у. д. ед.; при закупке партий в 2000 единиц (100 - 60) х 2000 = 80 000 у. д. ед. Если фирма располагает информацией о том, что с равной вероятностью может иметь место спрос как на 1000, так и на 2000 единиц товара, то среднеожидаемая прибыль (математическое ожидание прибыли) равна:
20 000 х 0, 5 + 80 000 х 0, 5 = 50 000 у. д. ед.
Если такая полная информация о покупательском спросе отсутствует и будет принято решение о закупке 1000 единиц товара при вероятности реализации этой партии 0, 5, то прибыль составит:
20 000 х 0, 5 = 10 000 у. д. ед.,
а при закупке 2000 единиц (при той же вероятности реализации):
80 000 х 0, 5 = 40 000 у. д. ед.
Следовательно, даже при более благоприятном варианте закупки 2000 единиц потери от неполноты информации равны:
50 000 - 40 000 = 10 000 у. д. ед.
1) Это и есть стоимость информации, т. е. та сумма, которую целесообразно израсходовать на изучение покупательского спроса. 2) Наиболее прибыльна закупка партии товара при наличии полной информации: в половине случаев следует закупать 1000 единиц товара, а в половине – 2000 единиц. 204. Обозначим вес большого арбуза через х, а стоимость одного килограмма его – через у. При этом стоимость большого и малого арбуза будет составлять:
Решая полученную систему из двух уравнений с двумя неизвестными, придем к квадратному уравнению:
Решая уравнение по стандартной формуле, получим:
x1 не подходит, так как общий вес покупки равен 14 кг. Следовательно, х2 = 10 – вес большого арбуза, а маленький арбуз весит 14-10 = 4 кг.
205. Обозначим капитал акционера А через х, а капитал акционера Б через у и составим два очевидных уравнения:
Решая совместно уравнения (1) и (2), найдем: х = 7 млн руб., у = 5 млн руб. 206. Проще всего решить эту задачу так. Мысленно включим в раздел еще один – восемнадцатый автомобиль. Тогда договорные доли от 18 автомобилей составят: для участника А – 9 автомобилей, для участника Б – 6 автомобилей, для участника В – 2 автомобиля. В сумме это и будет 17 автомобилей. Такой раздел не совсем точен, но понятен и по-своему справедлив. 207. Возраст фирмы Б равен: 31 -8 = 23 года. Возраст фирмы А: 23 х 2 = 46 лет. 208. Обозначив уставной фонд предприятия А через х, а уставной фонд предприятия Б через у, можем записать:
Из этого следует, что
Иными словами, уставной фонд предприятия Б в полтора раза больше, чем предприятия А. 209. Обозначив через х искомое количество акционеров, составим следующее очевидное уравнение:
Решение этого уравнения дает искомый ответ: х = 30 человек. 210. Вначале определим, какой процент от общего числа составляют отсутствующие акционеры:
Тогда процент, который составляли присутствующие акционеры, будет равен:
100 % - 16, 7 % = 83, 3 %. 211. Обозначим уставной фонд в рублях через х, тогда доля первого участника в уставном фонде составит
откуда следует, что х = 30 000 руб. Доля первого участника – 10 000 руб., доля второго – 7500 руб., доля третьего – 6000 руб. 212. Если обозначить время, которое прошло, через х, то оставшееся время будет равно
а всего в сутках
отсюда х = 8 часам (утра). 213. Обозначив возраст предприятия через х, можно записать условие задачи следующим образом:
откуда следует, что х = 48 годам.
214. На все привилегированные акции дивиденд составит:
6 х 5 % = 30 % от 100 млн руб., или 30 млн руб.
На все обыкновенные акции при этом останется для выплат дивидендов
100 млн руб.– 30 млн руб. = 70 млн руб.
Таким образом, на одну обыкновенную акцию придется дивиденд, равный
70 млн руб.: 28 = 2, 5 млн руб.
На одну привилегированную акцию дивиденд равен 5 % от 100 млн руб., т. е. 5 млн руб.
215. 1) Курс акций (Ка) рассчитывается по формуле:
где Д – дивиденд, СП – ссудный процент. ;
Курсовая стоимость акции 30 тыс. руб. 2) Учредительская прибыль (УП) рассчитывается по формуле:
где СЦк и СЦн – суммарная цена по курсу и по номиналу соответственно.
Стоимость единицы продукции равна:
1) При росте производительности труда в три раза будет выпускаться 30 единиц продукции в день, и стоимость единицы продукции станет
а стоимость массы продукции – 30 х 1 = 30 тыс. руб.
2) При увеличении интенсивности труда в два раза 10 единиц продукции будет производиться за полдня, а в день будет произведено 20 единиц продукции. Следовательно, стоимость единицы продукции станет
а стоимость массы продукции – 20 x 1, 5 = 30 тыс. руб.
217. 1) Норма прибыли (НП) рассчитывается по формуле:
где П – прибыль, З – затраты. С учетом того, что З = В - П, где В – величина выручки, получим:
Сумма эмиссии равна: П + 4 % П = 50 + 2 = 52 млн руб. 2) Общая стоимость привилегированных акций: 100 х 100 тыс. руб. = 10 млн руб. При этом на обыкновенные акции остается 52 - 10 = 42 млн руб., что дает возможность выпустить 42: 0, 5 = 84 обыкновенные акции.
218. 1) Курс акций рассчитывается по формуле (см. решение задачи 215):
Курсовая цена акции при этом 200 тыс. руб. 2) Учредительская прибыль рассчитывается по формуле (см. решение задачи 215):
219. Если бы у партнеров было 8 общих счетов, Семенов израсходовал бы их за 12 х 8 = 96 месяцев. А Семенов и Федоров за 96 месяцев израсходовали бы деньги с Теперь понятно, что за эти же 96 месяцев Федоров израсходовал бы деньги с 12 - 8 = 4 счетов. Отсюда получается, что один счет Федоров способен израсходовать за 220. 1 каменщик выложит 2 м стены за 4 часа, 1 м – за 2 часа, 5 м – за 10 часов; 2 каменщика выложат 5 м стены за 5 часов. 221. Все три проекта вполне реальны. Первый проект изучается странами Аравийского полуострова. Второй проект не экономичен: на каждый подъем и спуск аэростата расходуется много энергии. Третий проект запатентован и опробуется в нашей стране. 222. 1) Прибыль рассчитывается по формулам (см. решение задачи 171):
Для того чтобы 6, 1 % составили 1 млн руб., нужно получить доход (сумму выручки от реализации книги), равный
Для этого цена одной книги при тираже 100 тыс. экз. должна быть:
С учетом НДС: 164 + 20 % = 197 руб. 2) Авторский гонорар равен 3–5 % от 16, 4 млн руб., т. е. 492-820 тыс. руб. 3) На бумагу, картон и другие материалы будет выделено 20 % от 16, 4 млн руб., т. е. 3, 28 млн руб. 4) Типографские расходы составят 30 % от 16, 4 млн руб., т. е. 4 млн 920 тыс. руб. Издательские расходы составят 10–12 % от 16, 4 млн руб., т. е. 1 млн 640 тыс.– 1 млн 968 тыс. руб. 5) Торговым организациям придется заплатить 25 % от 16, 4 млн руб., т. е. 4 млн 100 тыс. руб. 6) Расходы на маркетинг, включая рекламу, равны 1 % от 16, 4 млн руб., т. е. 164 тыс. руб. 7) При установлении цены книги 300 руб. ее цена без учета НДС составит Сумма выручки от реализации книги будет 250 руб. х 0, 1 млн экз. = 25 млн руб. Чистая прибыль, равная 6, 1 % от 25 млн руб., составит 1 млн 525 тыс. руб.
223. 9 часов. 224. Предположим, рассматривается экономия энергетических ресурсов, эквивалентных 100 тоннам топлива. Тогда в результате реализации первого предложения можно будет обойтись 65 тоннами топлива (100 - 35 %), после реализации второго предложения – 32, 5 тонны (65 - 50 % от 65), после реализации третьего – 27, 7 тонны (32, 5 - 15 % от 32). Таким образом, общая экономия составит 100-27, 7 = 72, 3%. 225. Поскольку каждый должен вложить равную долю – 150 тыс. руб., то долг третьего компаньона первому составляет 230 - 150 = 80 тыс. руб., а второму – 220-150 = 70 тыс. руб. 226. Доля каждого предприятия составляет Отсюда стоимость 1 блока равна:
Из этого следует, что первое предприятие затратило 70 блоков по 3 тыс. у. д. ед., т. е. 210 тыс. у. д. ед.; второе – 40 блоков по той же цене, т. е. 120 тыс. у. д. ед.; третье, как известно, затратило 110 тыс. у. д. ед. Очевидно, что третье предприятие должно первому 100 тыс. у. д. ед. (210-110) и второму 10 тыс. у. д. ед. (120-110). 227. Наливаем в соответствующую емкость ровно 8 литров вина, из которой отливаем в 5-литровую ровно 5 (при этом в 8-литровой емкости остается ровно 3 литра). Из 5-литровой емкости вино переливаем в 12-литровую и в освободившийся сосуд наливаем оставшиеся в 8-литровой емкости 3 литра. Снова из 12-литровой заполняем вином 8-литровую емкость, из которой заливаем доверху 5-литровую (в которой уже есть 3 литра). При этом в 8-литровой емкости остается ровно 6 литров.
228. Обозначим новый результат фермера – количество ежедневно вспахиваемой земли – через х. Тогда величина участка будет равна 8х (теперь он вспахивает его за 8 дней), и условие задачи можно записать так:
Из этого следует, что 1) х = 10 га, 2) величина участка равна 8 х = 80 га. 229. Принимая количество автобусов, выпускаемых в день до реконструкции предприятия, можно записать условие задачи в виде следующего уравнения:
Отсюда х = 1, а количество автобусов, выпускаемых в день после реконструкции, равно х + 1 = 2. 230. Принимая количество изделий, выпускаемых в день по норме, за х, можно записать условие задачи в виде следующего уравнения:
откуда х = 2. Количество изделий, выпускаемых в день, фактически равно х + 3 = 5.
231. Принимая вес, потерянный яблоками после сушки, за х, можно записать условие задачи следующим образом:
Откуда х = 3, а искомый вес 4 т яблок после сушки равен 4 - 3 = 1 т. 232. Последовательность решения задачи такова: 1) Одна корова большого стада (70 коров) могла бы питаться травой 1680 дней (24 дня х 70 коров). 2) Одна корова малого стада (30 коров) могла бы питаться травой 1800 дней (60 дней х 30 коров). 3) Следовательно, за 36 дней (60 - 24) успевает нарасти трава, достаточная для питания одной коровы в течение 120 дней (1800-1680). 4) Значит, и за последующие 36 дней (96 -60) нарастет столько же травы, сколько хватит одной корове на 120 дней. 5) А всего количество дней, в течение которых могла бы питаться травой одна корова искомого стада, составит:
1800 + 120 = 1920 дней. 6) Зная, что коровы искомого стада будут питаться травой 96 дней, нетрудно найти, сколько в этом стаде коров: 1920 дней: 96 дней = 20 коров. 233. Первоначальное количество зеленой краски обозначим через х, тогда количество желтой составит 1 - х. После добавления 1 - х зеленой и х желтой краски количество красок разных цветов уравнялось (стало равным по 1). Следовательно, по 50 % краски каждого цвета.
234. В тонне сахара при влажности 15 % содержится 150 кг воды и 850 кг сухого вещества. После просушки количество воды уменьшилось на 80 кг и стало равно 70 кг. Следовательно, теперь влажность сахара составляет:
235. Вес жидкости в изделии до его сушки составлял 6 кг. Обозначая потери жидкости при сушке через х, можно записать условие задачи так:
Откуда х = 5, 45 кг. Следовательно, вес изделия после сушки равен: 60 - 5, 45 = 54, 55 кг.
236. В одной тонне переработанного сырья по условию задачи содержится 0, 17 т жидкости и 0, 83 т сухого вещества. С учетом этого обстоятельства и принимая за х вес испарившейся в процессе переработки жидкости, можно записать условие задачи так:
Откуда х= 1, 77 т. Следовательно, для того чтобы получить одну тонну продукта, нужно переработать сырья 1 + 1, 77 = 2, 77 т. 237. В 100 т морской воды по условию задачи содержится 6 т соли. С учетом этого обстоятельства и принимая за х количество пресной воды, необходимое для опреснения, можно записать условие задачи так:
Откуда х = 500 т.
238. В слитке сплава по условию задачи содержится 4 кг золота. С учетом этого обстоятельства и принимая за х количество золота, которое нужно добавить к слитку, можно записать условие задачи так:
Откуда х = 20 кг.
239. Принимая первоначальный вес сахара за х, а вес сахара после просушки за x1, можно записать условие задачи так:
Следовательно, вес высушенного сахара стал на 9 % меньше первоначального. 240. Раньше 5 деталей из 100 были с браком, теперь 1 деталь из 100. Следовательно, брак сократился на
|




















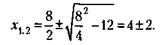




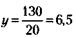













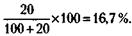
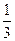 х, доля второго участника -
х, доля второго участника -  , доля третьего -
, доля третьего - 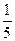 х, а весь уставной фонд будет равен:
х, а весь уставной фонд будет равен:

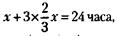


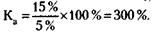

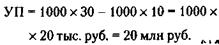












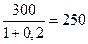 руб.
руб. блоков, которые стоят 110 тыс. у. д. ед.
блоков, которые стоят 110 тыс. у. д. ед.
 – старый результат фермера.
– старый результат фермера.