РЕШЕНИЯ 7 страница
241. Примем старое количество единиц продукции, выпускаемых в единицу времени, за 1. При этом время, затрачиваемое на единицу продукции, равно 1. Новое количество единиц продукции стало 1, 5. Значит, теперь время, затрачиваемое на единицу продукции, равно
243. Первый экскаватор проработал на 4 часа меньше нормы и в результате недоработал 40 % задания. Значит, первый экскаватор способен выполнить 100 %задания за
А за 8 часов первый экскаватор отработает 80 % задания. Это означает, что второй экскаватор за 8 часов выполнил 100 - 80 = 20 % задания. А 100 % задания второй экскаватор выполнит за
244. Принимая работу, выполненную бригадой № 1 в час, за единицу, можно записать, что обе бригады в час выполняют:
А за 10 часов обе бригады выполняют:
Следовательно, бригада № 1 смогла бы самостоятельно выполнить данную работу за 23: 1 = 23 часа, бригада № 2 - за 23: 1, 3 = 17, 7 часа.
245. Принимая сторону садового участка до увеличения за 1, получим его периметр, равный 4, а площадь – 1. С увеличением периметра на 20 % его стороны также вырастут на 20 % и станут равны 1, 2. Площадь при этом будет равна (1, 2)2 = 1, 44, т. е. вырастет на 44 %.
246. Принимая сторону садового участка до увеличения за единицу, получим его площадь, равную единице. Площадь участка с увеличением на 40 % его сторон станет равна 1, 4 х 1, 4 = 1, 96, т. е. вырастет на 96 %.
247. Принимая сторону прямоугольного садового участка до увеличения за единицу, получим его площадь, равную единице. С изменением сторон участка его площадь станет равна 1, 3 х 0, 7 = 0, 91, т. е. уменьшится на 9 %.
248. Находим, какие доли дома строительные организации строят за один год, и суммируем эти доли:
Исходя из того, что эта суммарная доля строится за 365 дней, рассчитываем (из пропорции), за сколько дней строится единица дома:
249.
250. Поскольку копия легче натуры в 8 миллионов раз и сделана из того же металла, то ее объем должен быть меньше объема натуры тоже в 8 миллионов раз. Но объемы тел относятся, как кубы их высот. Следовательно, копия должна быть ниже натуры в
Высота Эйфелевой башни около 300 м, поэтому высота копии должна быть 251. Поскольку объемы тел относятся, как кубы их линейных размеров, большая емкость должна быть в 252. Объем меньшего блока будет в 53 = 125 раз меньше. Следовательно, он будет весить
253. Обозначим через х количество спирта, который отлили в первый раз, и количество смеси, отлитой во второй раз. Тогда после первого отливания в емкости останется 100 - х спирта, а после доливания в нее воды в каждом литре смеси будет содержаться
литров спирта. После следующего отливания х литров смеси в емкости останется 100 - х литров смеси, в которой будет содержаться
литров спирта. Затем после второго доливания воды в емкости будет 100 литров смеси, из которых
Известно, что это соответствует 49-процентному раствору спирта:
Откуда х = 30 литров. 254. Примем площадь большого луга за единицу. Так как этот луг полдня косила вся артель и еще полдня – пол-артели, то, значит, за полдня пол-артели скашивает – большого луга. Следовательно, участок, не докошенный половиной артели на малом лугу, равен Это и есть дневная норма одного косца. А количество косцов в среднем можно найти, разделив то, что они выкосили за один день
255. Обозначим через х искомое количество граммов компонента коктейля с 50 % спирта, а через у – с 20 % спирта. Тогда условие задачи можно записать в виде следующего уравнения:
Из этого уравнения следует, что у = 2х, т. е. количество 50-процентного компонента коктейля должно быть в 2 раза меньше, чем 20-процентного. Так, в килограмме коктейля должно быть 333 г 50-процентного компонента и 667 г – 20-процентного.
256. Обозначив через х первоначальное количество топлива в баке «КамАЗа» и через у – в баке «Икаруса», можно составить по условиям задачи следующие два уравнения:
Совместное решение уравнений (1) и (2) приводит к ответу:
ПРИЛОЖЕНИЕ К РЕШЕНИЯМ
Таблица сложных процентов
|
= 0, 67, т. е. сократилось на 33 %.
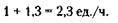
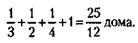
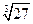= 3 раза выше и шире. Поверхности же подобных тел относятся как квадраты линейных размеров, т. е. поверхность большей емкости в З2 = 9 раз больше, а значит, и в 9 раз тяжелее.
литров составит спирт. Следовательно, процентное содержание спирта теперь равно
на дневную норму косца:
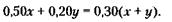
(1) (2)
