ОБЩИЕ СВЕДЕНИЯ. |
|
|

Заметки
А
Приложение А. Теория DAQ
В этом приложении содержится информация, полезная для пользователей DAQ-систем.
Темы
A. Теория датчиков
B. Схемы аналогового ввода-вывода
A. Теория датчиков
Один из первых шагов создания вашей DAQ-системы – выбор датчика. Выбранный вами датчик может повлиять на выбор других компонентов системы. Например, для некоторых датчиков требуется внешнее согласование сигнала для возбуждения и усиления, а другие могут использовать LabVIEW VI для преобразования результатов измерения напряжения в единицы температуры или деформации. Важно понимать, как работают различные типы датчиков, и знать их преимущества и недостатки. Ниже приведены сведения о наиболее распространенных датчиках: термопарах, терморезисторах, термисторах и датчиках деформации.
Термопары
Термопара – один из наиболее часто используемых температурных датчиков. Термопары очень надежны, недороги и работают в широком диапазоне температур. Термопары могут выдерживать температуры в несколько сотен градусов без потери своих свойств. Полупроводниковые датчики редко могут работать при температуре свыше 70 °C. Кроме того, термопары имеют небольшие размеры и могут быстро отслеживать изменения температуры.
Принцип действия термопары основан на том, что при соприкосновении двух разнородных металлов генерируется э.д.с. небольшого уровня, которая является функцией от температуры. Эта термо-э.д.с. называется напряжением Зеебека (в честь Томаса Зеебека, открывшего это явление в 1821 году). Для небольших изменений температуры это напряжение линейно, или
Δ V≈ SΔ T
где Δ V - изменение напряжения, S – коэффициент Зеебека, а Δ T - изменение температуры. S изменяется при больших изменениях температуры, что приводит к нелинейности выходных напряжений термопары в ее рабочем диапазоне, как показано на рисунке А-1. Поэтому вы должны использовать многочлены или таблицы для определения напряжения, соответствующего заданной температуре.
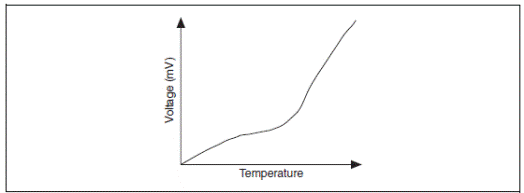
Рисунок A-1. Связь температуры и напряжения термопары
Существует несколько типов термопар. Они обозначаются заглавными буквами, которые указывают на их состав в соответствии с определениями Национального Института стандартов США. Например, у термопары типа J один вывод – железный, а второй из константана (медно-никелевый сплав).
На рисунке А-2 показана термопара. Точка, в которой термопара соединяется с вашей измерительной системой, называется точкой свободного спая. При подключении выводов термопары к выводам вашей системы, вы добавляете два дополнительных спая разнородных металлов, называемых холодным спаем. Холодный спай индуцирует термоэлектрическое напряжение в системе. Процесс устранения этого напряжения называется компенсацией холодного спая (cold junction compensation, CJC). Вы можете выполнить компенсацию холодного спая программно или аппаратно. Оба метода требуют измерения температуры в точке свободного спая с помощью датчика.

Рисунок A-2. Система с термопарой
Thermocouple – термопара, Reference Junction – точка свободного спая, Cold Junction – холодный спай, Measurement System - измерительная система
В таблице A-1 перечислены наиболее распространенные типы термопар. В таблице приведены два металла, образующих термопару, а также диапазон измерения температур.
Таблица A-1. Распространенные типы термопар
| Тип термопары | Проводник | Диапазон температур (°С) | Диапазон напряжений (мВ) | Коэффициент Зеебека (мкВ/°С) | |
| «Плюс» | «Минус» | ||||
| E | Хромель | Константан | от –270 до 1000 | от –9.835 до 76.358 | 58.70 при 0 °С |
| J | Железо | Константан | от –210 до 1200 | от –8.096 до 69.536 | 50.37 при 0 °С |
| K | Хромель | Алюмель | от –270 до 1372 | от –6.548 до 54.874 | 39.48 при 0 °С |
| T | Медь | Константан | от –270 до 400 | от –6.258 до 20.869 | 38.74 при 0 °С |
| S | Платина – 10%, Родий | Платина | от –50 до 1768 | от –0.236 до 18.698 | 10.19 при 600 °С |
| R | Платина – 13%, Родий | Платина | от –50 до 1768 | от –0.226 до 21.108 | 11.35 при 600 °С |
Особенности термопар:
· Недороги и надежны
· Выдерживают высокие температуры
· Могут отслеживать быстрые изменения температур
· Требуют компенсации холодного спая
· Очень маленькие напряжения (7 мкВ – 40 мкВ на градус Цельсия) – требуется усиление
· Нелинейный выход – необходима линеаризация измеренных напряжений
Терморезисторы (RTD)
Терморезистор – устройство, сопротивление которого меняется с температурой, как показано на рисунке А-3. Терморезисторы бывают из разных материалов и с разными сопротивлениями, самые популярные - 100-Омные платиновые терморезисторы. Как правило, терморезисторы более точны, чем термопары, и не требуют компенсации холодного спая. Однако терморезисторы обычно дороже, требуют линеаризации для повышения точности, а на результаты измерений с помощью терморезисторов могут влиять сопротивления выводов (например, длинные проводники).

Рисунок A-3. Связь температуры и сопротивления терморезистора
Существуют терморезисторы с двумя, тремя или четырьмя выводами. Двухпроводной терморезистор – самый простой, но может быть неточным из-за сопротивления выводов. Трехпроводной терморезистор использует третий провод для нейтрализации этого сопротивления. Четырехпроводной терморезистор (рисунок А-4) самый точный, поскольку также компенсирует ошибки из-за сопротивления выводов. Терморезистор подобен датчику деформации тем, что требует возбуждения для создания падения напряжения на резисторе. Обычно для этого используется источник тока.

Рисунок A-4. Четырехпроводной терморезистор
Current Source – источник тока
Вкратце, терморезистор обладает следующими характеристиками:
· Более точный, но более дорогой, чем термопары
· Не требует компенсации холодного спая
· Требует возбуждения – от оборудования согласования сигналов
· Требует линеаризации
· Двухпроводная конфигурация самая простая, но неточная из-за сопротивления выводов
· В трехпроводной и четырехпроводной конфигурации используются дополнительные провода для минимизации влияния сопротивления выводов
Датчики с интегральными схемами
Датчик с интегральной схемой – температурный датчик, изготовленный из кремниевого полупроводника, который ведет себя как чувствительный к температуре резистор. Датчики с интегральными схемами требуют внешнего источника энергии. Хотя они линейны и оправдывают затраты, у них низкое время реагирования и ограниченный температурный диапазон. Датчики с интегральными схемами часто используются для измерения температуры холодного спая при измерениях с помощью термопар.

Рисунок A-5. Связь температуры и сопротивления датчика с интегральной схемой
Temperature – температура, Voltage (mV) or Current (µA) – напряжение (мВ) или ток (мкА)
Термисторы
Термистор – устройство, сопротивление которого изменяется с температурой. Этот датчик представляет собой кусочек полупроводника из окиси металла, опрессованный в небольшой шарик, диск, пластинку или другую форму, полученный спеканием при высокой температуре и покрытый эпоксидной смолой или стеклом. Как показано на рисунке А-6, у термисторов нелинейный выход, и они требуют возбуждения. Поскольку термисторы обладают относительно высоким сопротивлением, для них не требуется трех- или четырехпроводного подключения.
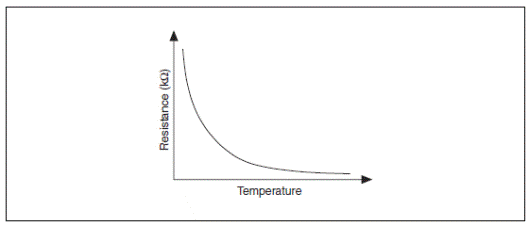
Рисунок A-6. Связь температуры и сопротивления термистора
Вкратце, термисторы обладают следующими характеристиками:
· Требуют возбуждения – от оборудования согласования сигналов
· Требуют линеаризации
· Обладают высокой чувствительностью
· Обладают высоким сопротивлением – не требуется трех- и четырехпроводной конфигурации.
Датчики деформации
Датчик деформации – устройство, используемое для обнаружения небольших движений в материалах из-за напряжения или вибрации. Датчики деформации состоят из тонких проводников, прикрепляемых к испытуемому материалу. Изменение сопротивления датчика указывает на деформацию материала. Во множестве датчиков используются элементы датчиков деформации, установленные на диафрагмах или в других конфигурациях, для определения различных физических величин. Например, тензодатчики – это датчики деформации, сконфигурированные для измерения веса.
Обычно датчики деформации используются с конфигурацией резисторов, называемой мостом Уитстона. В мосте четыре резистора располагаются в виде ромба. Когда вы подаете напряжение на мост, дифференциальное напряжение (Vm) с промежуточных узлов изменяется по мере изменения значений резисторов моста. Датчик деформации, как правило, поставляются с различными резисторами.
В датчиках деформации используются различные конфигурации моста – полномостовая, полумостовая и четверть-мостовая схемы подключения. Для датчика с полномостовой схемой подключения четыре резистора моста Уинстона физически расположены в самом датчике деформации. Для датчика с полумостовой схемой чувствительные элементы датчика обычно занимают два плеча моста Уинстона, а другие два плеча – это резисторы, устанавливаемые вами или находящиеся в устройстве согласования сигналов. На рисунке A-7 показан датчик деформации с полумостовой схемой. Сопротивление резистора R1 должно быть равно сопротивлению резистора R2, а Rg - значение сопротивления датчика деформации в ненагруженном состоянии. Хотя на рисунке А-7 показан источник питания постоянным напряжением, для некоторых датчиков деформации требуется питание током.

Рисунок A-7. Датчик деформация с полумостовой схемой
DC Voltage Excitation – напряжение постоянного тока, Physical strain gauge RG is value at rest – RG - сопротивление чувствительного элемента в ненагруженном состоянии, Supplied by signal conditioning hardware – устанавливается в устройстве согласования сигналов
B. Схема аналогового ввода-вывода
Чтобы вы лучше поняли, как DAQ-система преобразует напряжения реального мира в цифровые значения, которые ваш компьютер сможет отображать и анализировать, в этом разделе рассматриваются компоненты аналогового ввода вашего DAQ-устройства.
Инструментальный усилитель
Чтобы гарантировать максимальную точность АЦП, инструментальный усилитель усиливает входное напряжение до входного диапазона АЦП. Перемычки на плате и/или оборудование настраивают диапазон АЦП, а LabVIEW определяет используемый коэффициент усиления в соответствии с пределами входного сигнала. После усиления сигнала выход усилителя некоторое время (это время называется временем установления) колеблется, прежде чем стабилизируется в допустимом диапазоне относительно реального значения напряжения. Время установления влияет на то, как быстро вы можете точно брать отсчеты и зависит от используемого коэффициента усиления. На рисунке А-8 показаны характеристики времени установления стандартного инструментального усилителя. Обратите внимание, что проходит время установления ts, прежде чем усиленный сигнал стабилизируется в пределах допустимого диапазона напряжения (±% V). Необходимо позволить выходному сигналу усилителя установиться, прежде чем начинать аналого-цифровое преобразование. Если частота дискретизации (частота, с которой мультиплексор переключает каналы) превышает время установления инструментального усилителя, полученные данные могут быть неверными.

Рисунок A-8. Время установления
Time – время, Voltage – напряжение, %V Accuracy – погрешность
Например, рассмотрим DAQ-устройство с двумя входными сигналами, показанное на рисунке А-9. К каналу CH0 подключен сигнал напряжением +5 В, а к CH1 - напряжением –5 В. Это наихудший вариант - при переключении мультиплексора инструментальный усилитель увидит «ступеньку» в 10 В. Предположим, время установления усилителя равно 10 мкс, а используемая вами частота дискретизации составляет 2х105 Отсчетов/с. Усилитель не успевает войти в режим, а мультиплексор уже переключает канал для взятия следующего отсчета. Таким образом, в АЦП поступают неправильные напряжения.

Рисунок A-9. Эффект мультиплексирования сигналов инструментального усилителя
Analog Mux – аналоговый мультиплексор, Inst Amp – инструментальный усилитель, To S/H – к устройству выборки и хранения
На рисунке A-10 показаны сигналы с рисунка A-9, отсчеты которых берутся быстрее и медленнее времени установления. Обратите внимание, как АЦП оцифровывает неправильный уровень напряжения, если инструментальный усилитель не успевает войти в режим.

Рисунок A-10. Взятие отсчетов выполняется раньше, чем закончится время установления сигнала на выходе инструментального усилителя
Sample taken before amplifier has had time to settle – отсчет взят до того, как усилитель вошел в режим, Sample taken after amplifier has had time to settle – отсчет взят после того, как усилитель вошел в режим
В этом примере рассмотрен наихудший из возможный вариантов – инструментальному усилителю приходится переключаться через всю шкалу. Когда значения соседних входных сигналов находятся на определенном расстоянии друг от друга, время установления усилителя значительно меньше. Например, рассмотрим спецификацию платы AT-MIO-16X. Инструментальный усилитель этой платы имеет время установления 40 мкс при 16-разрядной точности. Вы можете правильно брать отсчеты сигналов, переключающихся между ±10 В с частотой 25 кГц (наихудший вариант). Однако если входные сигналы находятся в пределах 10 % диапазона полной шкалы друг от друга, время установления усилителя значительно меньше, и вы можете осуществлять выборку с максимальной частотой платы 100 кГц.
Воспользуйтесь следующими советами для уменьшения влияния времени установления:
· Задавайте порядок выборки так, чтобы усилитель испытывал как можно меньшую разность сигналов при переключении между каналами.
· Уменьшите сопротивление и емкость проводников, подключенных к плате сбора данных.
· Приобретите плату, инструментальный усилитель которой имеет меньшее время установления. Многие платы сбора данных National Instruments используют специализированный (заказной) инструментальный усилитель NI-PGIA, имеющий одинаковое время установления для всех коэффициентов усиления.
На рисунке А-11 сравниваются время установления NI-PGIA и покупного инструментального усилителя.

Рисунок A-11. Время установления NI-PGIA и готового инструментального усилителя
t (µs) – время (мкс), Resolution (bits) – разрешение (биты), Off-the-shelf Instrumentation Amplifier – покупной инструментальный усилитель
В спецификациях DAQ-устройства часто упоминается наименьший значащий бит (least significant bit, LSB). Наименьший значащий бит – это изменение напряжения, соответствующее изменению наименьшего значащего бита цифрового кода.
1 LSB = ((Входной диапазон АЦП / Коэффициент усиления))/2Разрядность АЦП
Например, AT-MIO-16X может установиться до ±0.5 LSB (или ±76.3 мкВ) при коэффициенте усиления 1 и входном диапазоне 10 В.
±0.5 LSB = [(10/1)/216] x 0.5 = 5/ 65536 = ±76.3 мкВ
АЦП
АЦП – основной компонент схемы аналогового ввода. АЦП оцифровывает аналоговый входной сигнал, то есть преобразует аналоговое напряжение в цифровые значения. АЦП хранит цифровое значение в буфере FIFO, пока оно не будет передано в память компьютера. При высокоскоростном сборе данных буфер FIFO предотвращает потерю данных из-за задержек обработки прерывания, которые могут произойти при передаче данных в память компьютера.
В DAQ-устройствах могут использоваться различные методы аналого-цифровых преобразований. Наиболее распространенные типы АЦП: с последовательным приближением, параллельный (flash), каскадный (half-flash), интегрирующий, с дельта-сигма модуляцией.
Последовательное приближение
АЦП с последовательным приближением – наиболее распространенный тип АЦП, используемый в DAQ-устройствах, поскольку отличается высокой скоростью и разрешением при умеренной цене. На рисунке А-12 показан 8-разрядный АЦП с последовательным приближением.

Рисунок A-12. АЦП с последовательным приближением
Ref Voltage – опорное напряжение, 8-bit DAC – 8-разрядный ЦАП, Comp – компаратор, Analog Input – аналоговый ввод, Successive Approximation Register (SAR) – регистр последовательного приближения, Start Conversion – начало преобразования, End of Conversion – конец преобразования, Control Logic – управляющая логика, n-bit Latch and Output Drivers – n-битный регистр-защелка и драйверы вывода, Digital Output (8bits) – цифровой выход (8 бит), Clock – тактовый генератор
Преобразователь с последовательным приближением использует технику, аналогичную взвешиванию предмета на весах. Например, пусть у вас есть 4 гири весом 1 г, 2 г, 4 г и 8 г. Вы помещаете предмет с неизвестным весом на одну чашу весов, а самый большой известный вес (гирю) – на другую. Если баланс не изменяется, вы добавляете следующую по величине гирю. Это повторяется, пока весы не придут в равновесие. Подсчитав суммарный вес всех гирь, вы узнаете вес предмета.
8-разрядный преобразователь с последовательным приближением работает аналогичным образом. Изначально все 8 бит ЦАП регистр установливает в 0. Далее, начиная с наибольшего значащего бита (MSB), каждый бит устанавливается в 1, и компаратор (Comp) оценивает выходное напряжение. Если напряжение ЦАП не превышает входное напряжение, бит остается в 1; в противном случае он устанавливается в 0. Цифровой код, представляющий входное напряжение – получается после того, как были протестированы все n бит. Для 8-битового АЦП этот процесс обычно занимает меньше 2 мкс. На рисунке А-13 показана последовательность преобразования для 8-разрядного АЦП с последовательным приближением.

Рисунок A-13. Последовательность преобразования для 8-разрядного АЦП с последовательным приближением
Clock Cycle – период тактового сигнала, DAC Output – выход ЦАП, Full Scale – полная шкала, Input Voltage – входное напряжение
Параллельный и каскадный
Параллельный АЦП – самый быстрый тип АЦП. Для n -битного АЦП входное напряжение подается одновременно на 2 n –1 компараторов. Как показано на рисунке А-14, каждый компаратор сравнивает входное напряжение с разным опорным значением. Значения опорных напряжений соседних компараторов различаются на один наименьший значащий бит. Если входное напряжение больше или равно опорному напряжению, компаратор выдает 1, в противном случае – 0. Шифратор переводит выходные сигналы компараторов в цифровой код.
Из-за большой стоимости и размера компонентов параллельные АЦП обычно имеют разрешение не больше 8 бит. В каскадных АЦП (вариации параллельных) используется гибридная техника, что позволяет создавать АЦП с меньшей стоимостью и большим разрешением, но б о льшим временем преобразования, чем параллельные АЦП.

Рисунок A-14. Параллельный АЦП
Ref Voltage – опорное напряжение, Input Signal – входной сигнал, 2n–1 Comparators – 2n–1 компараторов, Encoder – шифратор, n-bit Digital Code Output – n-разрядный цифровой код на выходе
Интегрирующий (двойного интегрирования)
Этот метод аналого-цифрового преобразования основан на интегрировании аналогового сигнала. У этого типа АЦП есть несколько преимуществ - высокое разрешение, хорошая линейность и подавление входных помех при помощи усреднения. Главный его недостаток – большое время преобразования. Поэтому интегрирующие АЦП обычно используются в цифровых мультиметрах и прочих измерительных устройствах, не требующих высокой скорости.
Дельта-Сигма модуляция
Самая передовая технология АЦП – дельта-сигма АЦП. В этих АЦП используются дельта-сигма модуляторы, а также дискретизация с запасом по частоте и цифровыми фильтрами для обеспечения высоких частот дискретизации, высокого разрешения и лучшей из всех типов АЦП линейности. Например, этот тип АЦП обладает 16-разрядным разрешением на частоте 48х103 Отсчетов/с без дифференциальной нелинейности.
Таблица A-2. Преимущества/использование различных типов АЦП
| Типы АЦП | Преимущества/Использование |
| С последовательным приближением | Высокое разрешение Высокая скорость Легко мультиплексировать Часто используется в платах DAQ Сигналы постоянного тока |
| Параллельный | Самая высокая скорость Отработанная технология Более дорогой |
| Интегрирующий | Высокое разрешение Хорошее подавление помех Хорошая линейность Отработанная технология Большое время преобразования Обычно используется в цифровых мультиметрах |
| Дельта-сигма | Высокое разрешение Отличная линейность Встроенная защита от искажения спектра Сигналы переменного тока |
Заметки
В
Приложение В. Обработка сигналов
В этой лекции излагаются основы обработки сигналов.
Темы
A. Дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ)
B. Информация об амплитуде и фазе
C. Разрешение по частоте и симметрия ДПФ/БПФ
D. Спектр мощности
E. Утечки спектра и сглаживающие окна
F. Характеристики различных типов оконных функций
G. Выбор типа окна, который необходимо использовать
H. Фильтрация
I. Идеальные фильтры
J. Реальные фильтры
K. Преимущество цифровых фильтров по сравнению с аналоговыми фильтрами
L. БИХ и КИХ фильтры
M. Фильтры с бесконечной импульсной характеристикой
N. Сравнение БИХ фильтров
O. Переходная характеристика БИХ фильтров
P. Фильтры с конечной импульсной характеристикой
A. Дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ)
Отсчеты сигнала, полученные с устройства ввода-вывода, являются представлением этого сигнала во временной области. Такое представление дает амплитуды сигнала в моменты его выборки. Во многих случаях вам в первую очередь может потребоваться частотный состав сигнала, а не амплитуды отдельных отсчетов. Как известно, описание сигнала в виде отдельных частотных составляющих называют представлением сигнала в частотной области. Данное представление позволяет более глубоко проанализировать сигнал и систему, которая его сформировала.
Алгоритм, используемый для преобразования отсчетов из временной области в частотную область, известен под названием «дискретное преобразование Фурье (ДПФ)». Такое преобразование устанавливает соответствие между отсчетами сигнала во временной области и их представлением в частотной области (рис. B-1). ДПФ применяют в таких областях как спектральный анализ, прикладная механика, акустика, рентгенография, численный анализ, измерительная техника и телекоммуникации.

Рисунок B-1. Дискретное преобразование Фурье
Time Domain Representation of x[n] – представление сигнала x[n] во временной области, Frequency Domain Representation – представление сигнала в частотной области
Если вы получаете с устройства ввода-вывода N отсчетов во временной области и применяете к ним ДПФ, то результатом являются также N отсчетов, но уже в частотной области.
Если сигнал подвергнуть дискретизации с некоторой частотой fs, то этой частоте соответствует интервал дискретизации Dt:

Дискретные сигналы обозначают как x[i], 0£ i£ N – 1 (таким образом, всего у вас N отсчетов). Если к этим N отсчетам применить дискретное преобразование Фурье, то результирующим представлением сигнала в частотной области будет (X[k], 0£ k£ N – 1).
 , (B-1)
, (B-1)
Обратите внимание на то, что представление сигнала во временной области x и представление сигнала в частотной области X состоят всего из N отсчетов. Аналогично интервалу Dt между отсчетами x во временной области в частотной области используют интервал Df между частотными составляющими X
 ,
,
который называют разрешением по частоте. Чтобы улучшить разрешение по частоте (уменьшить Df), следует увеличить количество отсчетов N, оставляя постоянной частоту дискретизации fs, или уменьшить частоту дискретизации fs при неизменном количестве отсчетов N.
Быстрое преобразование Фурье (БПФ) – это алгоритм, который применяется для быстрого вычисления ДПФ, когда количество отсчетов (N) равно степени числа 2. По количеству полученных отсчетов LabVIEW определяет, какой алгоритм использовать. Во всех VI LabVIEW применяется набор функций БПФ.
Пример вычисления ДПФ
Обозначим X[0] постоянную составляющую или среднее значение сигнала. Чтобы увидеть результат вычисления ДПФ по уравнению B-1, рассмотрим постоянный во времени сигнал с уровнем +1 В. На рис. B-2 показаны четыре отсчета этого сигнала.

Рисунок B-2. Отсчеты сигнала постоянного тока
Значение каждого из этих отсчетов равно +1, и они образуют временную последовательность

Рассчитав ДПФ этой последовательности по уравнению B-1 и применив формулу Эйлера

получим:




Как и следовало ожидать, все частотные составляющие, кроме постоянной составляющей X [0], равны нулю. Однако, вычисленное значение X [0] зависит от количества отсчетов N. В нашем случае для N =4 X [0] = 4. Если N =10, что в результате вычислений у вас получилось бы X [0]=10. Эта зависимость от N также имеет место для других частотных составляющих X [.]. Обычно для получения правильного значения уровня частотной компоненты результат ДПФ делят на N.
B. Информация об амплитуде и фазе
Вы уже видели, из N отсчетов входного сигнала получается N отсчетов ДПФ. Таким образом, количество отсчетов сигнала во временной и в частотной области одно и тоже. Как следует из уравнения B-1, независимо от того, действительные или комплексные отсчеты входного сигнала x [i], составляющие сигнала в частотной области X [k] всегда комплексные, хотя их мнимая часть может быть равна нулю. Поскольку ДПФ является комплексным, оно состоит из двух частей: амплитуды и фазы. Для реальных сигналов (отсчеты x [i] вещественные), которые поступают с выхода одного из каналов устройства ввода-вывода, ДПФ обладает симметрией относительно отсчета по частоте с номером N/2:
для амплитуды | X [k]| = | X [N–k]|,
для фазы Arg (X [k]) = – Arg (X [N–k])
Как известно, амплитуда X [k] является четной симметричной функцией, а фаза X [k] – нечетной симметричной функцией. Четной называют такую функцию, которая симметрична относительно оси y, а нечетной – функцию, которая симметрична относительно начала координат (рис. B-3).

Рисунок B-3. Четная симметрия (Even) и нечетная симметрия (Odd)
Такая симметрия ведет к дублированию информации, которая содержится в N отсчетах ДПФ. В связи с этим нужно вычислять или отображать только половину отсчетов ДПФ, а вторую половину можно получить за счет симметрии.

| Примечание: Если входной сигнал комплексный, ДПФ получается несимметричным, и таким методом пользоваться нельзя. |
C. Разрешение по частоте и симметрия ДПФ/БПФ
Если интервал дискретизации составляет Dt секунд и принято, что первый отсчет (при k = 0) соответствует моменту времени 0 секунд, k -й отсчет (k > 0, k – целое) соответствует моменту времени kDt секунд. Аналогично смысл разрешения по частоте  заключается в том, что k -я составляющая спектра ДПФ соответствует частоте kDf Гц. Это справедливо только для половины отсчетов. Другая половина описывает спектральные составляющие с отрицательными частотами. В зависимости от того, четно или нечетно количество отсчетов N, у вас может по-разному интерпретироваться частота, которая соответствует k -му отсчету ДПФ.
заключается в том, что k -я составляющая спектра ДПФ соответствует частоте kDf Гц. Это справедливо только для половины отсчетов. Другая половина описывает спектральные составляющие с отрицательными частотами. В зависимости от того, четно или нечетно количество отсчетов N, у вас может по-разному интерпретироваться частота, которая соответствует k -му отсчету ДПФ.
Четное число отсчетов
Предположим, что число отсчетов N четное. Введем обозначение  .
.
В таблице B-1 приведены частоты, которым соответствует каждый элемент комплексной последовательности (массива) X, полученной в результате ДПФ.
Таблица B-1. Соответствие частот элементам массива X
| Элемент массива | Частота |
| X [0] | постоянная составляющая |
| X [1] | Df |
| X [2] | 2 Df |
| X [3] | 3 Df |
| … | … |
| X [p–2] | (p –2) Df |
| X [p–1] | (p –1) Df |
| X [p] | pDf (частота Найквиста) |
| X [p+1] | –(p –1) Df |
| X [p+2] | –(p –2) Df |
| … | … |
| X [N–3] | –3 Df |
| X [N–2] | –2 Df |
| X [N–1] | –1 Df |
p-й элемент X [p] соответствует частоте Найквиста. Отрицательные элементы во втором столбце за пределами частоты Найквиста представляют собой отрицательные частоты.
Например, при N = 8, p = N /2 = 4 имеем:
| X [0] | постоянная составляющая |
| X [1] | Df |
| X [2] | 2 Df |
| X [3] | 3 Df |
| X [4] | 3 Df (частота Найквиста) |
| X [5] | –3 Df |
| X [6] | –2 Df |
| X [7] | – Df |
Значение амплитуд компонентов пар X[1] и X[7], X[2] и X[6], X[3] и X[5] одинаково. Различие между ними заключается в том, что X[1], X[2] и X[3] соответствуют положительным частотам, а X[5], X[6] и X[7] – отрицательным частотам. Следует учесть, что составляющей X[4] соответствует частота Найквиста.
Рассматриваемая комплексная последовательность частотных компонентов для N = 8 приведена на рис. B-4.

Рисунок B-4. Двустороннее преобразование для N = 8
Такую форму представления спектра, где видны спектральные составляющие и на положительных, и отрицательных частотах, называют двусторонним преобразованием Фурье.
Нечетное число отсчетов
Предположим, что число отсчетов N нечетное. Введем обозначение  . В таблице B-2 приведены частоты, которым соответствует каждый элемент комплексной последовательности (массива) X, полученной в результате ДПФ.
. В таблице B-2 приведены частоты, которым соответствует каждый элемент комплексной последовательности (массива) X, полученной в результате ДПФ.
Таблица B-2. Соответствие частот элементам массива X
| Элемент массива | Частота |
| X [0] | постоянная составляющая |
| X [1] | Df |
| X [2] | 2 Df |
| X [3] | 3 Df |
| … | … |
| X [p–1] | (p –1) Df |
| X [p] | |
| X [p+1] | |
| X [p+2] | –(p –1) Df |
| … | … |
| X [N–3] | –3 Df |
| X [N–2] | –2 Df |
| X [N–1] | – Df |
При нечетном N, значение N/2 является числом дробным. Следовательно, нет компонента, равного частоте Найквиста.
Например, при N = 7, p = (N– 1 ) /2 = (7–1)/2 = 3 имеем:
| X [0] | постоянная составляющая |
| X [1] | Df |
| X [2] | 2 Df |
| X [3] | 3 Df |
| X [4] | –3 Df |
| X [5] | –2 Df |
| X [6] | – Df |
Значение амплитуд компонентов пар X[1] и X[6], X[2] и X[5], X[3] и X[4] одинаково. Однако X[1], X[2] и X[3] соответствуют положительным частотам, а X[4], X[5] и X[6] – отрицательным частотам. Поскольку N является нечетным числом, на частоте Найквиста нет спектральной составляющей.
Рис. B-5 иллюстрирует приведенную выше таблицу для N = 7.

Рисунок B-5. Двустороннее преобразование для N = 7
Это тоже двустороннее преобразование Фурье, поскольку здесь есть спектральные составляющие и на положительных, и на отрицательных частотах.
Быстрые преобразования Фурье
Непосредственное применение ДПФ (уравнение B-1) к N отсчетам требует выполнения примерно N 2 сложных математических операций, и этот процесс занимает слишком много времени. Однако, если размер последовательности отсчетов является степенью числа 2,
 для m = 1, 2, 3, …
для m = 1, 2, 3, …
вы можете реализовать вычисление ДПФ с помощью примерно N log2 (N) операций. Это значительно ускоряет процесс выполнения ДПФ. В литературе по сигнальным процессорам (DSP) такие алгоритмы называют быстрыми преобразованиями Фурье (БПФ). БПФ – это быстродействующий алгоритм для вычисления ДПФ при количестве отсчетов (N), равном степени числа 2.
К преимуществам БПФ относятся быстрое выполнение и эффективное использование памяти, поскольку VI в процессе вычислений замещает ранее полученные данные новыми. Размер входной последовательности должен быть равен степени числа 2. Последовательность произвольного размера эффективно может выполнять ДПФ, однако ДПФ работает медленнее, чем БПФ, и использует больший объем памяти, поскольку в процессе его выполнения необходимо хранить промежуточные результаты.
Дополнение последовательности отсчетов нулями
Чтобы размер входной последовательности стал равными степени числа 2, ее дополняют нулями так, чтобы полное количество отсчетов равнялось ближайшей большей степени двойки. Например, имеющиеся у вас 10 отсчетов сигнала можно дополнить шестью нулями (рис. B-6), чтобы итоговое количество отсчетов стало равным 16 (=24).

Рисунок B-6. Дополнение последовательности отсчетов нулями
Original signal – исходный сигнал, Zero padded signal – сигнал, дополненный нулями
Помимо повышения быстродействия, дополнение количества отсчетов до степени двойки способствует также улучшению разрешения по частоте за счет увеличения количества отсчетов N (как вы помните,  ).
).
D. Спектр мощности
ДПФ или БПФ реального сигнала является комплексным, т.е. каждая спектральная составляющая имеет действительную и мнимую часть. Мощность каждой составляющей можно получить путем возведения в квадрат ее амплитуды. Поэтому мощность k -й спектральной составляющей (k -го элемента ДПФ/БПФ) записывается как | X [ k ]|2. Как известно, график, на который нанесены мощности каждой спектральной составляющей, называю
Дата добавления: 2014-11-12; просмотров: 965. Нарушение авторских прав; Мы поможем в написании вашей работы! |
|
|
|
|
Объект, субъект, предмет, цели и задачи управления персоналом Социальная система организации делится на две основные подсистемы: управляющую и управляемую...
|
Этапы и алгоритм решения педагогической задачи Технология решения педагогической задачи, так же как и любая другая педагогическая технология должна соответствовать критериям концептуальности, системности, эффективности и воспроизводимости...
|




