Изменение выходного напряжения трансформатора при изменении тока нагрузки. Внешняя характеристика трансформатора
Важной характеристикой трансформатора является внешняя характеристика, которая определяется зависимостью выходного напряжения от тока нагрузки. В случае трансформаторов эта зависимость определяется не только величиной сопротивления нагрузки, но и характером этой нагрузки (активно-индуктивным или активно-емкостным). Теоретически сопротивление нагрузки может быть представлено в комплексной форме. Тогда можно сказать, что вид внешней характеристики Для упрощения анализа характеристики в схеме замещения трансформатора пренебрежем цепью намагничивания трансформатора, что оправдано в случае мощных трансформаторов.
Если При одинаковом модуле сопротивления нагрузки фазовый сдвиг между выходным напряжением и током будет различным. Векторная диаграмма трансформатора для случая активно-индуктивной нагрузки представлена на рис. 5.17 и активно-емкостной нагрузки представлена на рис. 5.18.
Рис. 5.17 Рис. 5.18
При неизменном втором токе (токе вторичной обмотки) треугольник АВС, представляющий падение напряжения на сопротивлениях Пользуясь такой векторной диаграммой можно проследить изменение выходного напряжения при изменении коэффициента мощности нагрузки Если напряжение
Рис. 5.19 Из точки 0 проводят окружность радиусом, равным в масшта-бе На рис. 5.20 представлена упрощенная векторная диаграмма приведенного к вторичной обмотке трансформатора при резистивно-индуктивной нагрузке
Рис. 5.20
В реальных условиях длина вектора падения напряжения AC гораздо меньше напряжений OA и OC, которые пропорциональны
Эта формула определяет изменение напряжения на выходе трансформатора в функции коэффициента мощности
|

 зависит от модуля и аргумента сопротивления нагрузки.
зависит от модуля и аргумента сопротивления нагрузки. Рис. 5.16
Рис. 5.16
 , тогда
, тогда 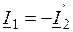 и схема замещения такого приведенного к вторичной обмотке трансформатора будет выглядеть так, как показано на рис. 5.16.
и схема замещения такого приведенного к вторичной обмотке трансформатора будет выглядеть так, как показано на рис. 5.16.
 и
и 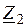 , останется неизменным. Направления векторов
, останется неизменным. Направления векторов  ,
,  ,
,  ,
,  сохранятся при изменении характера нагрузки.
сохранятся при изменении характера нагрузки. .
.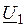 и ток
и ток  остаются неизменными, а аргумент сопротивления нагрузки
остаются неизменными, а аргумент сопротивления нагрузки  изменяется, изменение напряжения
изменяется, изменение напряжения  определяется следующим образом (рис. 5.19).
определяется следующим образом (рис. 5.19).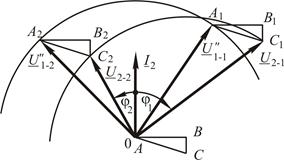
 . Для наглядности вектор
. Для наглядности вектор  расположен вертикально. Относительно
расположен вертикально. Относительно  из центра 0 строится треугольник короткого замыкания
из центра 0 строится треугольник короткого замыкания  . При этом катет
. При этом катет  пропорционален падению напряжения
пропорционален падению напряжения  , а катет
, а катет  пропорционален падению напряжения
пропорционален падению напряжения  . Из полученной точки
. Из полученной точки  проводится вторая окружность с радиу-сом
проводится вторая окружность с радиу-сом  (как и первая окружность). Последняя окружность является геометрическим местом конца вектора выходного напряжения
(как и первая окружность). Последняя окружность является геометрическим местом конца вектора выходного напряжения  . Диаграмма наглядно показывает влияние характера нагрузки на выходное напряжение. Так, при
. Диаграмма наглядно показывает влияние характера нагрузки на выходное напряжение. Так, при  выходное напряжение больше, чем при
выходное напряжение больше, чем при  (см. рис. 5.19). Таким образом, при изменении фазового сдвига между напряжением и током от
(см. рис. 5.19). Таким образом, при изменении фазового сдвига между напряжением и током от  до
до  до
до  . Вектор выходного напряжения при этом изменит положение от
. Вектор выходного напряжения при этом изменит положение от  до
до  . Нетрудно заметить то, что длина вектора выходного напряжения уменьшается.
. Нетрудно заметить то, что длина вектора выходного напряжения уменьшается. .
.
 и
и  или
или  , т. е. абсолютное приращение выходного напряжения в этом случае равно произведению тока на сумму, зависящую от сопротивлений потерь трансформатора и характера нагрузки. Относительное приращение напряжения, выраженное в процентах, определяется формулой
, т. е. абсолютное приращение выходного напряжения в этом случае равно произведению тока на сумму, зависящую от сопротивлений потерь трансформатора и характера нагрузки. Относительное приращение напряжения, выраженное в процентах, определяется формулой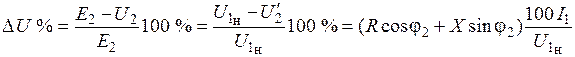 .
. Рис. 5.21
Рис. 5.21
 . График этой функции при неизменном токе нагрузки представлен на рис. 5.21. Поведение графика легко объясняется анализом векторной диаграммы, изображенной на рис. 5.19.
. График этой функции при неизменном токе нагрузки представлен на рис. 5.21. Поведение графика легко объясняется анализом векторной диаграммы, изображенной на рис. 5.19.


