Работа трансформатора в режиме нагрузки
Если к вторичной обмотке трансформатора подключить какое-либо устройство, потребляющее электрическую энергию, по ней потечет ток При увеличении намагничивающей силы вторичной обмотки намагничивающая сила первичной обмотки увеличивается, поддерживая практически постоянной их разность, которая равна намагничивающей силе тока холостого хода трансформатора. При неизменной величине суммарной намагничивающей силы рабочий магнитный поток трансформатора остается практически неизменным. С учетом того, что начальные фазы токов первичной и вторичной обмоток не совпадают, используя комплексную форму записи, получаем уравнение намагничивающих сил нагруженного трансформатора
где
Используя принцип независимости действия, можно сказать, что часть магнитного потока первичной обмотки, создаваемая намагничивающей силой Намагничивающая сила вторичной обмотки Результирующий магнитный поток сердечника равен сумме магнитных потоков обмоток Таким образом, во вторичной обмотке наводится две ЭДС: первая ЭДС
где Так как Заменяя ЭДС В предыдущем и настоящем разделах получены следующие уравнения для трансформатора:
Эти уравнения называются уравнениями равновесия трансформатора. Последнее уравнение иногда записывают в другой форме
Выраженные уравнениями связи между токами и напряжениями трансформатора удобно представлять векторной диаграммой, изображенной на рис. 5.7.
Рис. 5.7
Уравнение намагничивающих сил представлено векторной суммой Построение векторов По масштабу напряжения определяется длина векторов 5.6. Приведенный трансформатор и его схема В большинстве случаев коэффициент трансформации велик и имеет значение от нескольких единиц до сотен. Напряжение и ток первичной обмотки и соответствующие величины вторичной обмотки несоизмеримы. При анализе работы трансформатора желательно иметь дело с величинами одного порядка. С другой стороны, наличие магнитных связей в электрических цепях иногда затрудняет анализ работы электрических цепей. Поэтому реальный трансформатор заменяется другим трансформатором, коэффициент трансформации которого равен единице, но энергетические соотношения (мощности) остаются такими же, как и у исходного трансформатора. Преобразованный трансформатор называют приведенным. В зависимости от цели проводимого анализа работы трансформатора его «приводят» к первичной обмотке или к вторичной обмотке. У приведенного к первичной обмотке трансформатора параметры первичной обмотки остаются неизменными, параметры элементов вторичной обмотки изменяются с таким расчетом, чтобы мощности и их распределение между элементами оставались бы неизменными. Из условия сохранения мощностей можно сделать заключение о том, что фазовые соотношения между токами и напряжениями должны оставаться такими же, как и у исходного трансформатора. Все токи, напряжения и сопротивления вторичной обмотки преобразованного трансформатора называются приведенными к первичной обмотке. Аналогичным образом производится приведение трансформатора к вторичной обмотке. Рассмотрим процесс преобразования трансформатора. Ранее были представлены уравнения электрического и магнитного равновесия трансформатора
Уравнение намагничивающих сил
Обозначив Уравнение электрического равновесия для вторичной цепи имеет вид
Умножая уравнение на коэффициент трансформации
и Таким образом, результирующая система уравнений, определяющая соотношения в трансформаторе, примет вид
Введем следующие обозначения: а) б) в)
Для получения значений Окончательно имеем систему уравнений приведенного трансформатора
В соответствии с приведенной системой уравнений можно нарисовать схему замещения приведенного трансформатора (рис. 5.8).

Рис. 5.8 Векторная диаграмма приведенного трансформатора не отличается от диаграммы исходного трансформатора, необходимо заменить лишь величины Для расчета различных режимов работы трансформатора можно представить реальный трансформатор эквивалентной схемой. Такая цепь заменяет трансформатор лишь с точки зрения нагрузки в первичной цепи без трансформации. Из полученных уравнений:
так как
В соответствии с полученными уравнениями составим эквивалентную схему замещения приведенного трансформатора (рис. 5.9).

б Рис. 5.9
Связь между напряжением
где В схеме замещения резистор Таким образом, мы получили две разновидности схем замещения приведенного трансформатора (рис. 5.9, а и б).
Используя схему замещения, можно достаточно просто построить векторную диаграмму приведенного трансформатора (рис. 5.10). Построение векторной диаграммы удобно начать с вектора На практике часто используется схема замещения трансформатора, приведенного к вторичной обмотке. Такую схему замещения используют при анализе внешней характеристики трансформатора, показывающей изменение выходного напряжения при изменении тока нагрузки. Схема замещения такого трансформатора показана на рис. 5.11.
Рис. 5.11
В этой схеме ЭДС Коэффициент трансформации - Векторная диаграмма токов и напряжений трансформатора, приведенного к вторичной обмотке, будет выглядеть аналогично векторной диаграмме трансформатора, приведенного к первичной обмотке, и будет отличаться только масштабом изображения.
|

 , создавая свою намагничивающую силу
, создавая свою намагничивающую силу  . Направление этой магнитодвижущей силы (МДС) противоположно направлению МДС
. Направление этой магнитодвижущей силы (МДС) противоположно направлению МДС  первичной обмотки.
первичной обмотки. или
или  ,
, количество витков первичной и вторичной обмоток;
количество витков первичной и вторичной обмоток; токи первичной и вторичной обмоток трансформатора;
токи первичной и вторичной обмоток трансформатора; ток первичной обмотки ненагруженного трансформатора.
ток первичной обмотки ненагруженного трансформатора. , не сцепляется с вторичной обмоткой и замыкается не по сердечнику, а по воздуху
, не сцепляется с вторичной обмоткой и замыкается не по сердечнику, а по воздуху  . Вторая часть магнитного потока
. Вторая часть магнитного потока  первичной обмотки замыкается по сердечнику и сцепляется с вторичной обмоткой. Таким образом,
первичной обмотки замыкается по сердечнику и сцепляется с вторичной обмоткой. Таким образом,  .
. . Магнитные потоки
. Магнитные потоки  и
и 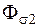 называют потоками рассеяния. Оба потока наводят в своих обмотках ЭДС
называют потоками рассеяния. Оба потока наводят в своих обмотках ЭДС  и
и  .
. .
.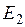 наводится основным магнитным потоком
наводится основным магнитным потоком 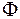 , а вторая ЭДС
, а вторая ЭДС  наводится магнитным потоком рассеяния
наводится магнитным потоком рассеяния  ,
, сопротивление провода вторичной обмотки (сопротивление меди), а
сопротивление провода вторичной обмотки (сопротивление меди), а  полное сопротивление нагрузки.
полное сопротивление нагрузки. (
( выходное напряжение трансформатора), то
выходное напряжение трансформатора), то  .
. падением напряжения на реактивном
падением напряжения на реактивном  , получаем
, получаем 
 .
.
 .
.
 . Вектор тока вторичной обмотки
. Вектор тока вторичной обмотки  на некоторый угол, определяемый характером нагрузки. Вектор падения напряжения на сопротивлении рассеяния
на некоторый угол, определяемый характером нагрузки. Вектор падения напряжения на сопротивлении рассеяния  совпадает по фазе с током
совпадает по фазе с током  . Построение векторов (
. Построение векторов ( ),
), 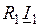 и
и  ведется по аналогичной методике.
ведется по аналогичной методике.
 может быть преобразовано. Разделим левую и правую части уравнения намагничивающих сил на количество витков первичной обмотки. В результате этого получаем
может быть преобразовано. Разделим левую и правую части уравнения намагничивающих сил на количество витков первичной обмотки. В результате этого получаем или
или 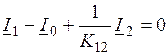 .
. , можем написать:
, можем написать:  .
. .
. , имеем:
, имеем:
 .
. ;
; ;
; .
.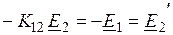 - ЭДС вторичной обмотки, приведенная к первичной обмотке;
- ЭДС вторичной обмотки, приведенная к первичной обмотке; приведенный ток вторичной обмотки;
приведенный ток вторичной обмотки;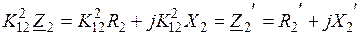 ,
, ;
;  ;
;  - сопротивления вторичной обмотки, приведенные к первичной обмотке.
- сопротивления вторичной обмотки, приведенные к первичной обмотке. необходимо изменить сопротивления
необходимо изменить сопротивления  ,
,  и
и  пропорционально квадрату коэффициента трансформации
пропорционально квадрату коэффициента трансформации  ;
; ;
;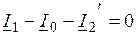 .
. ;
;  ;
;  ;
;  и
и  ,
, и
и  ;
; и
и  .
. может быть представлена в следующей форме:
может быть представлена в следующей форме: ,
, - сопротивление намагничивающей цепи.
- сопротивление намагничивающей цепи. представляет потери в сердечнике на перемагничивание и на вихревые токи.
представляет потери в сердечнике на перемагничивание и на вихревые токи.  выражает индуктивность первичной цепи и взаимную индуктивность. Представляя это сопротивление проводимостью
выражает индуктивность первичной цепи и взаимную индуктивность. Представляя это сопротивление проводимостью  , запишем
, запишем  .
.  и
и  отражают потери в сердечнике и индуктивность первичной обмотки.
отражают потери в сердечнике и индуктивность первичной обмотки. Рис. 5.10
Рис. 5.10
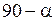 . Векторную диаграмму приведенной схемы часто называют векторной диаграммой приведенного трансформатора.
. Векторную диаграмму приведенной схемы часто называют векторной диаграммой приведенного трансформатора.
 , ток первичной обмотки
, ток первичной обмотки 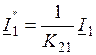 , сопротивления первичной обмотки
, сопротивления первичной обмотки  и
и  . Параметры параллельной ветви (
. Параметры параллельной ветви ( ,
,  и
и 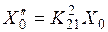 .
. .
.


