Анализ работы трансформаторов легче всего начать с анализа трансформатора, работающего в режиме холостого хода. Под режимом холостого хода понимается такой режим работы, когда ток вторичной обмотки равен нулю.
Если напряжение приложено к первичной обмотке, а вторичная обмотка разомкнута, то трансформатор работает вхолостую и представляет собой индуктивную катушку со стальным сердечником.
Ток холостого хода  , проходя по первичной обмотке трансформатора, за счет своей намагничивающей силы
, проходя по первичной обмотке трансформатора, за счет своей намагничивающей силы  создает магнитный поток, который можно представить в виде суммы двух магнитных потоков: магнитного потока рассеяния
создает магнитный поток, который можно представить в виде суммы двух магнитных потоков: магнитного потока рассеяния  (рис. 5.5), который не сцепляется со вторичной обмоткой, и основного магнитного потока
(рис. 5.5), который не сцепляется со вторичной обмоткой, и основного магнитного потока 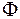 , который сцепляется как с первичной, так и
, который сцепляется как с первичной, так и
со вторичной обмоткой.

Рис. 5.5
 Рис. 5.6
Рис. 5.6
|
Изменяющийся по синусному закону во времени магнитный поток 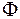 наводит в обмотках ЭДС. ЭДС обмотки, магнитный поток которой изменяется по синусоидальному закону во времени
наводит в обмотках ЭДС. ЭДС обмотки, магнитный поток которой изменяется по синусоидальному закону во времени
и которая имеет 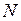 витков, пропорциональна произведению количества витков и производной магнитного потока
витков, пропорциональна произведению количества витков и производной магнитного потока
во времени  . В первичной обмотке
. В первичной обмотке  и во вторичной обмотке
и во вторичной обмотке  . Обе ЭДС синусоидальной формы отстают от магнитного потока на четверть периода (рис. 5.6).
. Обе ЭДС синусоидальной формы отстают от магнитного потока на четверть периода (рис. 5.6).
Магнитный поток рассеяния наводит в первичной обмотке ЭДС рассеяния  .
.
Можно предположить, что мгновенное значение тока первичной обмотки определяется из формулы 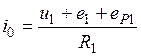 или
или  .
.
Уравнение мгновенных значений напряжений дает уравнение напряжений первичной обмотки в векторной форме
 .
.
Магнитный поток рассеяния пропорционален току первичной обмотки, так как не сцепляется с вторичной обмоткой, а величина ЭДС  может рассматриваться как падение напряжения на реактивном сопротивлении индуктивности рассеяния первичной обмотки
может рассматриваться как падение напряжения на реактивном сопротивлении индуктивности рассеяния первичной обмотки  .
.
Уравнение напряжений первичной обмотки примет вид
 .
.
Сопротивление 
 называется внутренним сопротивлением первичной обмотки.
называется внутренним сопротивлением первичной обмотки.
Для понимания электромагнитных процессов в трансформаторе, для понимания фазовых соотношений электрических и магнитных величин удобно использовать векторную диаграмму напряжений и токов (см. рис. 5.6).
Ток холостого хода может рассматриваться как векторная сумма активного тока  , связанного с потерями, и реактивного тока
, связанного с потерями, и реактивного тока  , который связан с намагничиванием сердечника. Векторная диаграмма трансформатора, работающего в режиме холостого хода, изображена на рис. 5.6.
, который связан с намагничиванием сердечника. Векторная диаграмма трансформатора, работающего в режиме холостого хода, изображена на рис. 5.6.
Векторы ЭДС 
 и
и  отстают от вектора магнитного потока на 90 °. Для определения входного напряжения
отстают от вектора магнитного потока на 90 °. Для определения входного напряжения 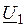 необходимо воспользоваться уравнением напряжения:
необходимо воспользоваться уравнением напряжения: 
=  .
.
Вектор  находится в противофазе с
находится в противофазе с  , вектор падения напряжения
, вектор падения напряжения  совпадает с вектором тока
совпадает с вектором тока  по фазе, а вектор падения напряжения на сопротивлении рассеяния
по фазе, а вектор падения напряжения на сопротивлении рассеяния  опережает вектор тока
опережает вектор тока  на 90 °.
на 90 °.
Исследования силовых трансформаторов показывают, что при полной нагрузке трансформатора падение напряжения на внутреннем сопротивлении первичной обмотки составляет несколько процентов от номинального напряжения. В свою очередь ток холостого хода правильно спроектированного трансформатора состав-
ляет 3 …10 % от номинального входного тока. Падение напря-
жения на внутреннем сопротивлении первичной обмотки при прохождении тока холостого хода составляет менее процента от номинального напряжения первичной обмотки. По этой причине можно допустить, что  и
и  , т. е. напряжения на зажимах трансформатора, работающего в режиме холостого хода, практически равны электродвижущим силам соответствующих обмоток. Коэффициент трансформации при таком допущении может быть вычислен отношением напряжений на обмотках трансформатора, работающего в режиме холостого хода. Энергия, потребляемая трансформатором в режиме холостого хода, расходуется на потери в сердечнике и на потери в обмотках. У трансформатора, нагруженного на номинальную нагрузку, потери в обмотках составля-
, т. е. напряжения на зажимах трансформатора, работающего в режиме холостого хода, практически равны электродвижущим силам соответствующих обмоток. Коэффициент трансформации при таком допущении может быть вычислен отношением напряжений на обмотках трансформатора, работающего в режиме холостого хода. Энергия, потребляемая трансформатором в режиме холостого хода, расходуется на потери в сердечнике и на потери в обмотках. У трансформатора, нагруженного на номинальную нагрузку, потери в обмотках составля-
ют 2-0, 25 % номинальной мощности, у ненагруженного же трансформатора эти потери пренебрежительно малы по сравнению с потерями в сердечнике. Поэтому мощность потерь в сердечнике трансформатора 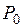 может быть определена как мощность, потребляемая трансформатором в режиме холостого хода.
может быть определена как мощность, потребляемая трансформатором в режиме холостого хода.

 , проходя по первичной обмотке трансформатора, за счет своей намагничивающей силы
, проходя по первичной обмотке трансформатора, за счет своей намагничивающей силы  создает магнитный поток, который можно представить в виде суммы двух магнитных потоков: магнитного потока рассеяния
создает магнитный поток, который можно представить в виде суммы двух магнитных потоков: магнитного потока рассеяния  (рис. 5.5), который не сцепляется со вторичной обмоткой, и основного магнитного потока
(рис. 5.5), который не сцепляется со вторичной обмоткой, и основного магнитного потока 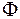 , который сцепляется как с первичной, так и
, который сцепляется как с первичной, так и 
 Рис. 5.6
Рис. 5.6
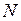 витков, пропорциональна произведению количества витков и производной магнитного потока
витков, пропорциональна произведению количества витков и производной магнитного потока  . В первичной обмотке
. В первичной обмотке  и во вторичной обмотке
и во вторичной обмотке  . Обе ЭДС синусоидальной формы отстают от магнитного потока на четверть периода (рис. 5.6).
. Обе ЭДС синусоидальной формы отстают от магнитного потока на четверть периода (рис. 5.6). .
. 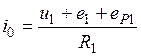 или
или  .
. .
. может рассматриваться как падение напряжения на реактивном сопротивлении индуктивности рассеяния первичной обмотки
может рассматриваться как падение напряжения на реактивном сопротивлении индуктивности рассеяния первичной обмотки  .
. .
.
 называется внутренним сопротивлением первичной обмотки.
называется внутренним сопротивлением первичной обмотки. , связанного с потерями, и реактивного тока
, связанного с потерями, и реактивного тока  , который связан с намагничиванием сердечника. Векторная диаграмма трансформатора, работающего в режиме холостого хода, изображена на рис. 5.6.
, который связан с намагничиванием сердечника. Векторная диаграмма трансформатора, работающего в режиме холостого хода, изображена на рис. 5.6. и
и  отстают от вектора магнитного потока на 90 °. Для определения входного напряжения
отстают от вектора магнитного потока на 90 °. Для определения входного напряжения 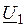 необходимо воспользоваться уравнением напряжения:
необходимо воспользоваться уравнением напряжения: 
 .
. находится в противофазе с
находится в противофазе с  совпадает с вектором тока
совпадает с вектором тока  по фазе, а вектор падения напряжения на сопротивлении рассеяния
по фазе, а вектор падения напряжения на сопротивлении рассеяния  опережает вектор тока
опережает вектор тока  и
и  , т. е. напряжения на зажимах трансформатора, работающего в режиме холостого хода, практически равны электродвижущим силам соответствующих обмоток. Коэффициент трансформации при таком допущении может быть вычислен отношением напряжений на обмотках трансформатора, работающего в режиме холостого хода. Энергия, потребляемая трансформатором в режиме холостого хода, расходуется на потери в сердечнике и на потери в обмотках. У трансформатора, нагруженного на номинальную нагрузку, потери в обмотках составля-
, т. е. напряжения на зажимах трансформатора, работающего в режиме холостого хода, практически равны электродвижущим силам соответствующих обмоток. Коэффициент трансформации при таком допущении может быть вычислен отношением напряжений на обмотках трансформатора, работающего в режиме холостого хода. Энергия, потребляемая трансформатором в режиме холостого хода, расходуется на потери в сердечнике и на потери в обмотках. У трансформатора, нагруженного на номинальную нагрузку, потери в обмотках составля-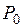 может быть определена как мощность, потребляемая трансформатором в режиме холостого хода.
может быть определена как мощность, потребляемая трансформатором в режиме холостого хода.


