СВОЙСТВА ЧАСТОСТИ1. 2. Частость достоверного события равна 1. Wn(U)=1. 3. Частость суммы попарно несовместных событий равна сумме частостей. Рассмотрим систему Ai, i=1,..., k; события попарно несовместны, т.е.
Пусть в результате некоторого испытания произошло событие A. По определению сумы это означает, что в этом испытании произошло некоторое событие Ai. Так как все события попарно несовместны, то это означает, что никакое другое событие Aj (i¹ j) в этом испытании произойти не может. Следовательно:
Над наблюдаемым полем событий F задается счетно-аддитивная мера - числовая скалярная функция, элементами которой являются элементы поля F, т.е. события. Она удовлетворяет следующим трем условиям-аксиомам теории вероятности. 1. 2. P(A) Î [0, 1] P(U)=1. 3. Пусть имеется A1, A2, A3,..., Ak - система попарно несовместных событий
Набрать следующий ниже текст с формулами и произвести аналогичное форматирование.
|
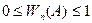
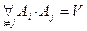Событие 
, 
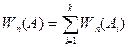
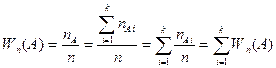(1)
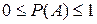. P(A) - число, принадлежащее сегменту [0, 1] и называющееся вероятностью наступления события A.
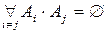Если 
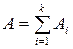, то 
.
