Обоснование формулы условной вероятности в общем случае
Пусть в nB испытаниях произошло событие B, а в nA испытаниях произошло событие A. Найдем условную частость наступления события A при условии, что произошло событие B. Мы можем сделать это для обоснования формулы, т.к. под вероятностью наступления события понимается предел частости наступления события при условии, что серия испытаний достаточно длинная. Условная частость:
События A1A2...Ak называются независимыми между собой, если вероятность их совместного наступления
Два независимых события совместны.
Для экзамена доказать самим формулу суммы произвольного числа событий
Сложное событие B определяет все возможные комбинации исходов двух испытаний независимо друг от друга. В результате первого испытания произошли элементарные события: В результате второго испытания события:
Набрать следующий ниже текст с формулами и произвести аналогичное форматирование.
Вероятностные характеристики дискретных случайных величин
Математическим ожиданием случайной величины X называется число вида
где xi - все возможные различные конкретные исходы испытания; pi - вероятности их наступления. Математическое ожидание является как бы аналогом центра масс точечной механической системы:
Как центр масс:
Смысл характеристики мат. ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной. Свойства математического ожидания
1. MC=C
2. MCX=CMX Построим таблицу для случайной величины CX:
Набрать следующий ниже текст с формулами и произвести аналогичное форматирование.
РАСЧЕТ
|

 (1)
(1)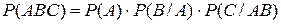 (2)
(2) (3)
(3) (4)
(4) (5)
(5) .
. .Тогда:
.Тогда:  .
.  , т.к. второе испытание не влияет на результаты первого.
, т.к. второе испытание не влияет на результаты первого. (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)


