ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ. ПРОВЕРКА ПРОЧНОСТИ ДЛЯ СЛОЖНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ
Рекомендуемая литература Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 13 (§ 13.6). Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 3 (§ 10, 11), гл. 4 (§ 14, 15, 20). Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 3 (§ 3.1–3.5, 3.7), гл. 8 (§ 8.1, 8.2). Основные понятия и формулы Напряженное состояние в точке тела. Под точкой тела понимаем малый объем материала вблизи геометрической точки. Внутри этого объема напряжения изменяются дифференциально мало. Н апряженным состоянием в точке называют совокупность напряжений на всех площадках, проведенных через нее. Напряженное состояние задают три вектора напряжений на трех взаимно перпендикулярных площадках. Эти три Пусть введена прямоугольная система координат и три площадки, перпендикулярные ее осям x, y, z. Векторы напряжений на этих трех площадках задаются своими проекциями на оси координат и обозначаются соответственно Следствием условий равновесия элементарного объема тела является закон парности касательных напряжений: С учетом закона парности касательных напряжений для задания напряженного состояния в точке нужно указать шесть параметров: три нормальных напряжения В точке всегда можно выбрать три взаимно перпендикулярные площадки, на которых действуют только нормальные напряжения, а касательные напряжения равны нулю. Эти площадки называют главными, действующие на них нормальные напряжения – главными напряжениями. Для главных напряжений, занумерованных по убыванию, используется специальное обозначение: Главные напряжения обладают свойством экстремальности: одно из них максимально среди нормальных напряжений на площадках с произвольной нормалью Главными направлениями напряженного состояния называют направления нормалей к главным площадкам. Эти направления обозначают цифрами 1, 2, 3. Главные площадки обозначают соответственно 1, 2, 3. Напряженное состояние, при котором ни одно из трех главных напряжений не равно нулю, называется объемным. Если одно из главных напряжений равно нулю, то напряженное состояние называется плоским. При линейном напряженном состоянии отлично от нуля только одно главное напряжение. Далее рассматривается плоское напряженное состояние. Пусть главная площадка с нулевым главным напряжением расположена перпендикулярно оси y. Тогда при плоском напряженном состоянии отличны от нуля напряжения Аналитическое исследование плоского напряженного состояния. Заданы напряжения на взаимно перпендикулярных площадках. Вычисляются напряжения на площадках произвольной ориентации, главные площадки и главные напряжения, площадки, по которым действуют экстремальные касательные напряжения.
Правила знаков для напряжений: нормальное напряжение На двух взаимно перпендикулярных площадках заданы напряжения
Наклонная площадка перпендикулярна чертежу, ее положение определяет угол Нормальное напряжение
В правой части формул на первом месте в разности Из выражения (2.2а) следует, что сумма нормальных напряжений на двух взаимно перпендикулярных площадках не изменяется при повороте этих площадок:
Когда заданные площадки являются главными, формулы (2.2а) и (2.2б) принимают вид
Здесь Главные напряжения вычисляются по формуле
Согласно (2.3)
Положение главных площадок определяет угол
Формуле (2.7) отвечает множество углов Для определения площадки, на которой действует бó льшее из напряжений
и посмотреть на ее знак. Если В рассматриваемом случае плоского напряженного состояния три главных напряжения таковы: Максимальное среди касательных напряжений на всевозможных площадках, проведенных через точку, таково:
Это напряжение действует на площадке, одинаково наклоненной к площадкам 1 и 3. Соответствующее нормальное напряжение
Касательное напряжение, максимальное по модулю среди напряжений на площадках, перпендикулярных плоскости чертежа, таково:
Соответствующее нормальное напряжение
В общем случае величины Графическое исследование плоского напряженного состояния. Вместо вычислений по приведенным выше формулам можно построить круг напряжений Мора и произвести графические построения. В этом заключается графическое решение задачи (см. примеры). Деформированное состояние в точке. Деформированным состоянием в точке называют совокупность линейных деформаций всевозможных элементарных отрезков, проходящих через точку, и изменений углов между всевозможными парами этих отрезков. Пусть Деформированное состояние в точке определяют шесть параметров: три линейных деформации
и три угловых деформации Через точку всегда можно провести три взаимно перпендикулярных отрезка, углы между которыми не изменятся при деформации. Оси координат, направленные вдоль этих отрезков. называют главными осями деформации. Связь между напряжениями и деформациями. Для изотропного материала (свойства материала одинаковы во всех направлениях) при не слишком большом уровне напряжений связь напряжений и деформаций описывает обобщенный закон Гука:
Здесь Для изотропного материала главные оси деформации и напряженного состояния совпадают, поэтому линейные деформации вдоль главных осей определяются соотношениями (2.13):
Соответствующие угловые деформации равны нулю. Относительная объемная деформация
Оценка прочности. Прочность материала в точке проверяется по соответствующей материалу теории прочности. Из большого числа ныне существующих теорий прочности при выполнении студенческих задач используются перечисляемые ниже. Под исчерпанием прочности подразумевается переход материала в предельное состояние, то есть разрушение для хрупкого материала и возникновение пластической деформации для пластичного материала. Расчет должен обеспечивать нормативный запас прочности, что достигается введением коэффициента запаса прочности, понижающего разрешаемый уровень напряжений.[5] Для всех применяемых при выполнении расчетно-графической работы теорий прочности условие прочности можно записать в едином виде
где Согласно первой теории прочности, справедливой для хрупких материалов, разрушение происходит от отрыва при достижении максимальным напряжением
Вторая теория прочности также применяется к хрупким материалам. Согласно этой теории разрушение происходит от отрыва при достижении максимальной деформацией
Третья теория прочности определяет уровень напряжений, при котором в пластичном материале возникают заметные остаточные деформации. Согласно этой теории переход материала в предельное состояние происходит от сдвига при достижении максимальным касательным напряжением
Согласно четвертой теории прочности пластическое деформирование возникает от сдвига при достижении энергией изменения формы предельного значения. Условием прочности служит соотношение
Непосредственно эта теория прочности не определяет положения опасных площадок. Последние (на основании иной трактовки теории) можно считать равно наклоненными к главным осям (октаэдрические площадки). Условие прочности, соответствующее теории прочности Мора (пятой теории прочности), имеет вид
Здесь К оценке прочности хрупких материалов применяются первая, вторая и пятая теории прочности. Однако результаты оценки заметно различаются. Наиболее достоверна оценка по пятой теории прочности. Третья и четвертая теории прочности применяются к оценке прочности пластических материалов, дают близкие оценки прочности и широко используются в инженерных расчетах.
|

 ,
,  ,
,  . Проекции, перпендикулярные площадкам, называются нормальными напряжениями
. Проекции, перпендикулярные площадкам, называются нормальными напряжениями  ,
,  ,
,  . Индекс в обозначении указывает направление нормали
. Индекс в обозначении указывает направление нормали  к площадке. Проекции, лежащие в плоскостях площадок, называются касательными напряжениями
к площадке. Проекции, лежащие в плоскостях площадок, называются касательными напряжениями 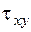 ,
,  ,
,  ,
, 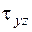 ,
,  ,
, 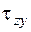 . Первый индекс обозначения определяет площадку, на которой действует напряжение, второй индекс указывает ось, в направлении которой напряжение действует.
. Первый индекс обозначения определяет площадку, на которой действует напряжение, второй индекс указывает ось, в направлении которой напряжение действует. ;
; 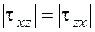 ;
;  . Касательные напряжения
. Касательные напряжения  ,
,  направлены либо навстречу друг другу, либо в противоположные стороны.
направлены либо навстречу друг другу, либо в противоположные стороны. ,
,  ,
,  ,
,  ,
,  . Обозначение предполагает
. Обозначение предполагает  (с учетом знака).
(с учетом знака).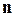 , другое – минимально. В принятых обозначениях
, другое – минимально. В принятых обозначениях  ,
,  . Пусть
. Пусть  – вектор напряжения на площадке с нормалью
– вектор напряжения на площадке с нормалью  – его модуль. Свойство экстремальности означает также следующее:
– его модуль. Свойство экстремальности означает также следующее:  .
. Рис. 2.2. Напряжения
на наклонной площадке
Рис. 2.2. Напряжения
на наклонной площадке

 Рис. 2.1. Плоское напряженное
состояние в точке тела
Рис. 2.1. Плоское напряженное
состояние в точке тела
 положительно, если направление напряжения совпадает с направлением внешней нормали
положительно, если направление напряжения совпадает с направлением внешней нормали 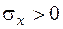 ,
,  (растягивающие), касательное напряжение
(растягивающие), касательное напряжение  (обходит площадку по часовой стрелке), касательное напряжение
(обходит площадку по часовой стрелке), касательное напряжение  (обходит площадку против часовой стрелки). При указанном правиле знаков закон парности касательных напряжений имеет вид
(обходит площадку против часовой стрелки). При указанном правиле знаков закон парности касательных напряжений имеет вид . (2.1)
. (2.1) между нормалью к ней и осью x (см.рис. 2.2). Угол
между нормалью к ней и осью x (см.рис. 2.2). Угол  на наклонной площадке определяются формулами
на наклонной площадке определяются формулами ; (2.2а)
; (2.2а) . (2.2б)
. (2.2б) стоит нормальное напряжение на площадке, от нормали к которой отсчитан угол
стоит нормальное напряжение на площадке, от нормали к которой отсчитан угол  , (2.3)
, (2.3) – нормальное напряжение на площадке, перпендикулярной площадке с нормалью n.
– нормальное напряжение на площадке, перпендикулярной площадке с нормалью n. (2.4)
(2.4) ,
, 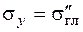 – главные напряжения.
– главные напряжения. . (2.5)
. (2.5)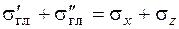 . (2.6)
. (2.6) , который находится из уравнения
, который находится из уравнения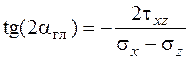 . (2.7)
. (2.7) ,
,  .
. ,
,  , нужно вычислить вторую производную
, нужно вычислить вторую производную . (2.8)
. (2.8) при
при  , то на этой площадке действует меньшее из напряжений
, то на этой площадке действует меньшее из напряжений  . (2.9)
. (2.9) .
. . (2.10)
. (2.10)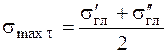 . (2.11)
. (2.11) ,
,  различны.
различны.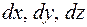 – длины до деформации трех взаимно перпендикулярных элементарных отрезков, расположенных вдоль осей
– длины до деформации трех взаимно перпендикулярных элементарных отрезков, расположенных вдоль осей  .
. 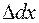 ,
,  ,
,  – изменения этих длин в результате деформации.
– изменения этих длин в результате деформации. ,
,  ,
,  ,
, ,
,  ,
,  , представляющих собой изменения прямых углов между отрезками
, представляющих собой изменения прямых углов между отрезками 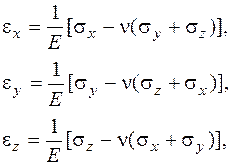
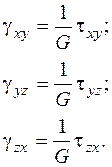 (2.13)
(2.13) ,
,  ,
,  – упругие характеристики материала.
– упругие характеристики материала. 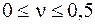 );
);  .
. ,
, , (2.14)
, (2.14)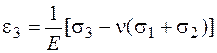 .
.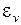 в точке есть отношение абсолютного изменения объема элементарного параллелепипеда к его первоначальному объему. Связь объемной деформации
в точке есть отношение абсолютного изменения объема элементарного параллелепипеда к его первоначальному объему. Связь объемной деформации  . (2.15)
. (2.15)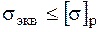 , (2.16)
, (2.16) – допускаемое напряжение. Величина
– допускаемое напряжение. Величина  представляет собой предельный уровень напряжения и определяется из эксперимента. Для хрупких материалов она совпадает с пределом прочности при осевом растяжении, для пластичных материалов – с пределом текучести при осевом растяжении. n – нормируемый коэффициент запаса прочности.
представляет собой предельный уровень напряжения и определяется из эксперимента. Для хрупких материалов она совпадает с пределом прочности при осевом растяжении, для пластичных материалов – с пределом текучести при осевом растяжении. n – нормируемый коэффициент запаса прочности.  – комбинация главных напряжений
– комбинация главных напряжений  . (2.17)
. (2.17) (она должна быть положительной) предельного значения. Деформации вплоть до момента разрушения считаются малыми и вычисляются по закону Гука. Плоскость отрыва (опасное сечение) перпендикулярна направлению действия главного напряжения
(она должна быть положительной) предельного значения. Деформации вплоть до момента разрушения считаются малыми и вычисляются по закону Гука. Плоскость отрыва (опасное сечение) перпендикулярна направлению действия главного напряжения  . (2.18)
. (2.18) . (2.19)
. (2.19) . (2.20)
. (2.20)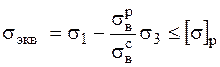 . (2.21)
. (2.21) ,
,  – пределы прочности при растяжении и при сжатии. По теории Мора можно определить и положение опасных площадок. Соответствующая формула не приводится.
– пределы прочности при растяжении и при сжатии. По теории Мора можно определить и положение опасных площадок. Соответствующая формула не приводится.


