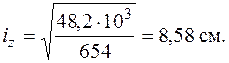Ось  – ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату
– ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату 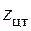 по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I, III и прямоугольник II (см. рис. 5.18). Площадь фигуры
по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I, III и прямоугольник II (см. рис. 5.18). Площадь фигуры

Для определения статического момента выберем вспомогательную ось 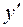 , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе
, проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе  :
:

Тогда по (5.15)

Откладываем эту координату и проводим через центр тяжести (точку С на рис. 5.18) главную центральную ось  .
.
Найдем моменты инерции всей фигуры относительно осей  и
и  , складывая (или вычитая) моменты инерции составляющих фигур:
, складывая (или вычитая) моменты инерции составляющих фигур:
 ;
;
 .
.
Для определения момента инерции каждой из фигур I, II и Ш используем формулы изменения моментов инерций при параллельном переносе осей (5.16), (5.17). Моменты инерции прямоугольника II и треугольников I и Ш относительно собственных центральных осей 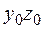 (см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
(см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
 Рис. 5.18. К определению моментов инерции
симметричной фигуры
Рис. 5.18. К определению моментов инерции
симметричной фигуры
|




В заключение вычислим радиусы инерции относительно главных центральных осей по формулам (5.10) и построим эллипс инерции.

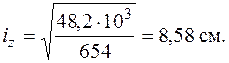
Эллипс инерции показан на рис. 5.18.

 – ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату
– ось симметрии фигуры (рис. 5.18) – является главной осью инерции. Найдем положение второй главной центральной оси, определив положение центра тяжести фигуры. Очевидно, что центр тяжести лежит на оси симметрии, поэтому найдем только координату 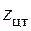 по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I, III и прямоугольник II (см. рис. 5.18). Площадь фигуры
по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I, III и прямоугольник II (см. рис. 5.18). Площадь фигуры
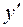 , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе
, проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Чтобы найти статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в системе  :
:

 .
. ;
; .
.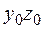 (см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
(см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда Рис. 5.18. К определению моментов инерции
симметричной фигуры
Рис. 5.18. К определению моментов инерции
симметричной фигуры