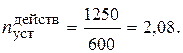Решение. Сечение стержня состоит из уголков (прокатного профиля), поэтому используем для подбора сечения метод последовательных попыток

Сечение стержня состоит из уголков (прокатного профиля), поэтому используем для подбора сечения метод последовательных попыток. Поскольку в условии устойчивости имеем сразу две неизвестные величины ( и ), то одной из них задаемся произвольно. Удобно задаться . Тогда из условия устойчивости (6.6) найдем

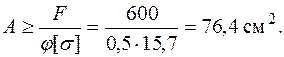
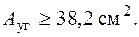Площадь одного уголка Из сортамента прокатной стали выбираем уголок, удовлетворяющий этому условию. Отметим, что в сортаменте может быть несколько уголков с примерно одинаковой площадью: уголки с длинной полкой и тонкой стенкой и уголки с короткой, но более толстой стенкой. Выбирать следует самые тонкие уголки, так как при одинаковой площади радиус инерции у тонких уголков больше и, следовательно, гибкость стержня с сечением из тонкого уголка меньше, а чем меньше гибкость, тем более устойчив стержень. В рассматриваемом примере выберем уголок 180´ 11, площадь которого 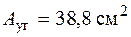. Найдем радиусы инерции относительно главных центральных осей y и z, которыми являются оси симметрии сечения (см. рис. 6.4, б). Следует ожидать, что радиус инерции относительно оси y будет минимальным, так как материал ближе расположен к оси y, чем к оси z. Убедимся в этом.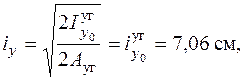

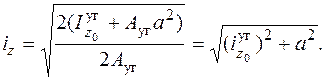
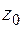Радиус инерции одного уголка относительно оси берем из сортамента: 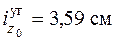, а расстояние а (см. рис. 6.4, б) сосчитаем:

Таким образом, очевидно, что

и

Теперь найдем гибкость стержня[18]

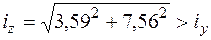
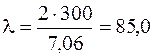
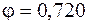и из таблицы, интерполируя, найдем . Проверим условие устойчивости: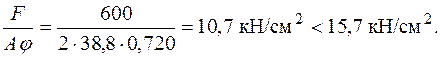

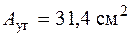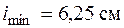Условие устойчивости выполняется, но сечение не является экономичным, поэтому сделаем еще попытку. Уменьшим размеры сечения и примем самый тонкий уголок их тех, у которых длина полки 160 мм, а именно, уголок 160´ 10. , и гибкость стержня

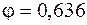По таблице находим и видим, что условие устойчивости выполняется с небольшим запасом:

Сечение из двух уголков 160´ 10 можно считать экономичным[19]. Условие прочности для подобранного сечения тоже выполняется, поскольку согласно условию .

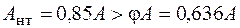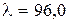В заключение найдем действительный коэффициент запаса устойчивости. Поскольку стержень с подобранным сечением из уголков 160´ 10 имеет гибкость , находящуюся в пределах между и , то определяем критическую силу по формуле Ясинского:

 

Действительный коэффициент запаса устойчивости