Методи оцінки фінансових ризиків підприємства
Найважливішим показником, що характеризує міру фінансового ризику підприємства, є його рівень, що впливає на формування рівня прибутковості фінансових операцій підприємства. Ці показники перебувають у тісному взаємозв'язку і являють собою єдину систему: «прибутковість-ризик». Співвідношення рівнів прибутковості і ризику є однієї з основних базових концепцій аналізу фінансових ризиків, відповідно до якої рівень прибутковості фінансових операцій завжди супроводжується підвищенням рівня їх ризику і навпаки. Рівень характеризує ймовірність виникнення фінансового ризику під впливом певного фактору ризику (або групи факторів ризику) і можливі фінансові втрати при появі ризикової події. На підставі цього, формується конкретний методичний інструментарій оцінки рівня ризику, що дозволяє вирішувати основні завдання аналізу фінансових ризиків підприємства (рис. 12.3).
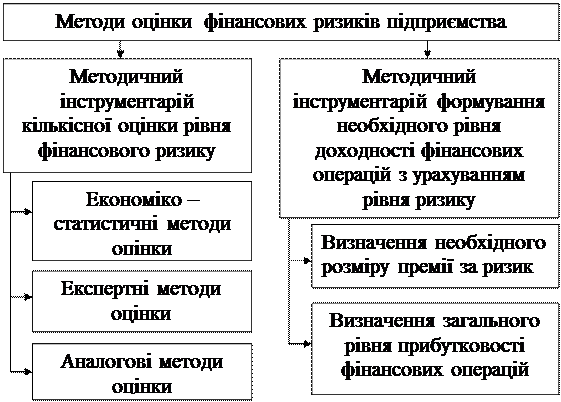
Рис. 12.3. Методи оцінки фінансових ризиків підприємства.
Методичний інструментарій кількісної оцінки рівня фінансового ризику містить у собі: різноманітні економіко-статистичні, експертні, аналогові методи. Вибір конкретних методів оцінки визначається наявністю необхідної інформаційної бази та рівнем кваліфікації аналітиків. 1. Економіко-статистичні методи оцінки – є основою оцінки рівня фінансового ризику. До них відносяться наступні показники: 1.1) Рівень фінансового ризику – характеризує загальний алгоритм оцінки рівня певного виду ризику та розраховується за формулою:
де РФР – рівень певного фінансового ризику; ІР – імовірність виникнення певного фінансового ризику; РВ – розмір фінансових витрат при виникненні певного ризику. При застосуванні даного методу розмір можливих фінансових втрат виражається абсолютною сумою, а імовірність виникнення фінансового ризику – коефіцієнтом (варіації, бета-коефіцієнтом та ін.). Рівень фінансового ризику, за даним алгоритмом, буде виражений абсолютним показником, що істотно знижує базу його порівняння при розгляді альтернативних варіантів. 1.2) Дисперсія – характеризує ступінь коливання досліджуваного показника (доходу (прибутку) від здійснення фінансової операції) стосовно його середньої величини. Розрахунок дисперсії здійснюється за формулою:
де σ 2 – дисперсія; Ri – конкретне значення можливих варіантів очікуваного доходу за певною фінансовою операцією;
Pi – можлива частота (імовірність) одержання окремих варіантів очікуваного доходу за певною фінансовою операцією; n – число спостережень.
1.3) Середньоквадратичне відхилення – визначає ступінь коливання досліджуваного показника. Розраховується за наступною формулою:
де σ – середньоквадратичне відхилення.
Приклад: Необхідно оцінити рівень фінансового ризику за інвестиційною операцією. На розгляд представлено два альтернативних інвестиційних проекти (проект «А» і проект «В») з імовірністю очікуваних доходів (табл. 12.5). Таблиця 12.5 Розподіл імовірності отримання доходів за інвестиційними проектами «А» і «В»
Висновок: Порівнюючи дані за інвестиційними проектами, можна побачити, що розрахункові значення доходів за проектом «А» коливаються в межах від 200 до 600 тис. грн. при сумі очікуваних доходів у 450 тис. грн. За проектом «В» сума очікуваних доходів також становить 450 тис. грн., однак їх коливання здійснюється у діапазоні від 100 до 800 тис. грн. Це дозволяє зробити висновок, що ризик реалізації інвестиційного проекту «А» нижче, ніж проекту «В», де коливання розрахункового доходу вище. Більше наочне подання про рівень ризику дають результати розрахунку середньоквадратичного (стандартного) відхилення, представлені у табл. 12.6, результати свідчать про те, що: середньоквадратичне (стандартне) відхилення за інвестиційним проектом «А» становить 150, за інвестиційним проектом «В» – 221, що вказує на більший рівень його ризику. 1.4) Коефіцієнт варіації – дозволяє визначити рівень ризику, за умови, що показники середнього очікуваного доходу від здійснення фінансових операцій розрізняються між собою. Розраховується за формулою: Таблиця 12.6 Розрахунок середньоквадратичного (стандартного) відхилення за двома інвестиційними проектами
де CV – коефіцієнт варіації; σ – середньоквадратичне (стандартне) відхилення;
Приклад: Необхідно розрахувати коефіцієнт варіації за трьома інвестиційними проектами при різних значеннях середньоквадратичного (стандартного) відхилення і середнього очікуваного значення доходу. Вхідні дані наведені у табл. 12.7. Таблиця 12.7 Розрахунок коефіцієнту варіації за наявними інвестиційними проектами
Висновок: Результати розрахунку показують, що найменше значення коефіцієнта варіації – за проектом «А», а найбільше – за проектом «Д». Таким чином, хоча очікуваний дохід за проектом «Д» на 33% вище, ніж за проектом «А» Отже, при порівнянні рівнів ризиків за окремими інвестиційними проектами перевагу варто віддавати тому з них, за яким значення коефіцієнтів варіації нижче. Це свідчить про найкраще співвідношення прибутковості і ризику. 1.5) Бета-коефіцієнт – дозволяє оцінити індивідуальний або портфельний (систематичний) фінансовий ризик. Використовується для оцінки ризиків інвестування в окремі цінні папери. Розраховується за формулою:
де β – бета-коефіцієнт; К – ступінь кореляції між рівнем прибутковості за певним видом цінних паперів і середнім рівнем прибутковості даної групи фондових інструментів на ринку; σ і – середньоквадратичне відхилення прибутковості за індивідуальним видом цінних паперів; σ р – середньоквадратичне відхилення прибутковості на фондовому ринку. Рівень фінансового ризику певних видів цінних паперів визначається на основі наступних значень бета-коефіцієнтів: β = 1 – середній рівень; β > 1 – високий рівень; β < 1 – низький рівень. 2. Експертні методи оцінки рівня фінансового ризику – застосовуються за умов відсутності на підприємстві необхідних інформативних даних для використання економіко-статистичних методів. Ці методи базуються на опитуванні кваліфікованих фахівців (страхових, фінансових, інвестиційних менеджерів та інших експертів) із подальшою математичною обробкою результатів проведеного опитування. Для отримання більш розгорнутої характеристики рівня ризику, опитування спрямовується на окремі види фінансових ризиків, ідентифіковані за досліджуваною операцією (відсотковий, валютний, інвестиційний і ін.). У процесі такої оцінки кожен експерт оцінює рівень можливого ризику, ґрунтуючись на бальній шкалі: – ризик відсутній: 0 балів; – ризик незначний: 10 балів; – ризик нижче середнього рівня: 30 балів; – ризик середнього рівня: 50 балів; – ризик вище за середнє рівня: 70 балів; – ризик високий: 90 балів; – ризик дуже високий; 100 балів.
3. Аналогові методи оцінки рівня фінансового ризику – дозволяють визначити рівень ризиків за окремими (найбільш масовими) фінансовими операціями підприємства. Для порівняння може бути використаний як власний, так і зовнішній досвід здійсненні таких фінансових операцій. Методичний інструментарій формування необхідного рівня доходності фінансових операцій з урахуванням рівня ризику – дозволяє забезпечити чітку кількісну пропорційність зазначених показників у процесі управління фінансовою діяльністю підприємства. 2.1) При визначенні необхідного рівня премії за ризик використовується наступна формула:
де RPn – рівень премії за ризик за певним фінансовим (фондовим) інструментом; Rn – середня норма прибутковості на фінансовому ринку; Аn – безризикова норма прибутковості на фінансовому ринку; β – бета-коефіцієнт, що характеризує рівень систематичного ризику за певним фінансовим (фондовим) інструментом. Приклад: Необхідно розрахувати рівень премії за ризик за трьома видами акцій. Вхідні дані наведені у табл. 12.8. Таблиця 12.8 Розрахунок необхідного рівня премії за ризик за наявними акціями
Висновок: Результати розрахунку свідчать про те, що рівень премії за ризик зростає пропорційно до росту значення бета-коефіцієнту, тобто рівня систематичного ризику. 2.2) При визначенні необхідної суми премії за ризик використовується формула:
де RPs – сума премії за ризик за конкретним фінансовим (фондовим) інструментом у справжній вартості; SI – вартість певного фінансового (фондового) інструменту; RPn – рівень премії за ризик за певним фінансовим (фондовим) інструментом (виражений десятковим дробом). Приклад: Виходячи з ціни трьох акцій, які котируються на ринку, і результатів розрахунку рівня премії за ризик (табл. 12.8), визначити суму премії за кожною акцією. Вхідні дані наведені у табл. 12.9. Таблиця 12.9 Розрахунок необхідної суми премії за ризик за наявними акціями
Висновок: Результати розрахунку показують, що найменше значення коефіцієнта варіації – за проектом «А», а найбільше – за проектом «Д». Таким чином, хоча очікуваний дохід за проектом «Д» на 33% вище, ніж за проектом «А» 2.3) При визначенні (необхідного) загального рівня прибутковості фінансових операцій з урахуванням фактору ризику використовується формула:
де RDn – необхідний загальний рівень прибутковості за конкретним фінансовим (фондовим) інструментом з урахуванням фактору ризику; Аn – безризикова норма прибутковості на фінансовому ринку; RPn – рівень премії за ризик за конкретним фінансовим (фондовим) інструментом. Приклад: Варто розрахувати необхідний загальний рівень прибутковості за трьома видами акцій. Вхідні дані наведені у табл. 12.10. Таблиця 12.10 Розрахунок необхідного загального рівня прибутковості за наявними акціями
Висновок: за даними, наведеними у табл. 12.10 можна зробити висновок, що найбільший необхідний загальний рівень прибутковості відзначений за акцією 3 (13, 4 %).
|

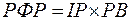 , (12.1)
, (12.1)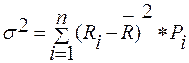 , (12.2)
, (12.2) – середнє очікуване значення доходу за певною фінансовою операцією;
– середнє очікуване значення доходу за певною фінансовою операцією;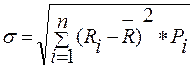 , (12.3)
, (12.3)
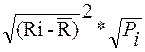
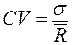 ; (12.4)
; (12.4)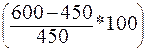 , рівень ризику за ним, обумовлений коефіцієнтом варіації, вище на 61%
, рівень ризику за ним, обумовлений коефіцієнтом варіації, вище на 61% 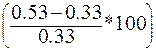 .
.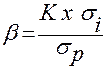 , (12.5)
, (12.5) 
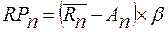 , (12.6)
, (12.6)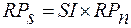 , (12.7)
, (12.7)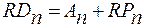 , (12.8)
, (12.8)


