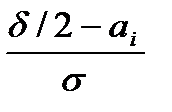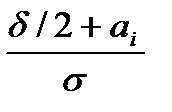Глава 3.2. Оценка точности технологического процесса изготовления КЭ
Для анализа производственных погрешностей применяются различные методы, которые позволяют оценить точность выбранного технологического процесса. Наиболее часто применяются аналитический и статистический методы оценки точности. Аналитический метод требует математического описания всех первичных факторов влияющих на погрешность обработки, метод достаточно трудоёмкий и применяется в отдельных случаях. Статистический метод основан на положениях теории вероятности и математической статистики, при этом анализируются как закономерно изменяющиеся, случайные факторы влияющие на погрешность изготовления, так и систематические погрешности. Для анализа точности выбранного технологического процесса производят измерение фактических размеров партии деталей и строят кривую распределения. Разность между минимальным и максимальным фактическими размерами измеренных деталей разбивают на равные интервалы. Определяют количество размеров деталей в каждом интервале. Построение кривой производят в следующей последовательности. На оси абсцисс обозначают поле рассеивания размеров, которое определяется как разность между фактическим максимальным и минимальным размерами Хф.мах – Хф.мин. = Хф, полученными в результате измерений, в выбранном масштабе.. Хф – фактическое поле рассеивания размеров при обработке деталей. Полученное поле рассеивания делят на n интервалов. Из середины каждого интервала, по оси ординат, откладывают относительную частоту W = m /N, где m– количество размеров деталей попавших в данный интервал, N – общее количество деталей в измеряемой партии. По полученным точкам строят ломанную кривую фактического распределения размеров см. рис.2.3.2 Чем больше партия деталей тем плавнее становится ломанная кривая, и по своему виду приближается к кривой закона нормального распределения (кривой Гаусса) описываемой уравнением Y = j(х) = где
общее количество деталей в партии, n – количество интервалов. Рис.2.3.2 Х ср = На график наносят величину поля допуска Определяется величина смещения центра группирования размеров относительно середины поля допуска
При оценке точности технологического процесса, основным условием является выполнение следующих
Рис. 2.3.3. требований: аi = 0, Подбор оборудования для автоматического получения размеров в границах заданного поля допуска обычно производится таким образом, чтобы в этих границах укладывалась вся практически существенная часть кривой распределения. При соблюдении этих двух условий за границы поля допуска будет выходить только 0, 27% всех изготовленных изделий – количество, которое обычно принимается за несущественное, тем более, что половина этого количества является исправимым браком. На практике возможны различные случаи рассеивания размеров в следствие одновременного влияния различных производственных факторов.
Рис.2.3.4 На рис. 2.3.5 и рис. 2.3.6 приведены случаи, когда поле рассеивания больше (
Рис.2.3.5 Рис. 2.3.6 Как видно из графиков в первом случае появляются две зоны Аi и Бi, площадь которых соответствует определённому проценту брака, исправимого и неисправимого. Во втором случае брак отсутствует, так как все отклонения размеров находятся в пределах поля допуска. В случае если присутствует систематическая погрешность Рис. 2.3.7 и Рис. 2.3.8, при Следовательно, если хотя бы одна из границ поля рассеивания 6
Рис. 2.3.7 Рис. 2.3.8 Площадь А Аi = 0, 5 [1 – Ф(ta)] где ta = Площадь Б Бi = 0, 5 [1- Ф(tб)} где tб = аi – смещение центра группирования относительно середины поля допуска. Значение функции Лапласа Ф(t) определяют из таблицы.
|

 е -
е - 
 - средне квадратичное отклонение случайной величины аргумента определяется по формуле
- средне квадратичное отклонение случайной величины аргумента определяется по формуле


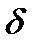 = Хд.мах - Хд.мин, где Хд.мах и Хд.мин соответственно минимально и максимально допустимые отклонения размера детали, величина заданная конструктором.
= Хд.мах - Хд.мин, где Хд.мах и Хд.мин соответственно минимально и максимально допустимые отклонения размера детали, величина заданная конструктором.


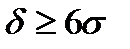 . Из теории вероятности и математической статистики известно, что в интервале 6
. Из теории вероятности и математической статистики известно, что в интервале 6  ) настройка станка обычно производится на середину поля допуска.
) настройка станка обычно производится на середину поля допуска.
 .
.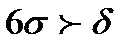 ) или меньше (
) или меньше ( ), чем поле заданного допуска.
), чем поле заданного допуска.