Эквивалентная электрическая схема
Обычно в технических системах информация представляется в виде электрического напряжения или тока. Для преобразования выходного сопротивления потенциометра Rx в электрическое напряжение Ux, потенциометр может быть включён в электрическую цепь (рис. 2.3).
Рис. 2.3 Выходное напряжение потенциометра Ux поступает на вход услительно-преобразовательных устройств. Входные цепи этих устройств являются нагрузкой потенциометра и представляются сопротивлением нагрузки R Н. Величина сопротивления нагрузки влияет на функцию преобразования R=f(x). А) Если R Н > > R 0, то потенциометр работает без нагрузки, и
В случае линейной зависимости между расстоянием х и сопротивлением Rx, мы можем записать:
Подставляя (2.3) в (2.2), получим:
Б) Если R Н ≈ R 0, то можно использовать теорему об эквивалентном генераторе и представить соответствующую схему замещения датчика (рис. 2.4).
Рис. 2.4
На рис.2.4 R Э это выходное внутреннее сопротивление датчика, которое определяется, как сопротивление схемы относительно выходных клемм при закороченном источнике напряжения U:
Выходное напряжение датчика
где U Э= С учётом (2.5) получим
где По уравнению (2.7) на рис. 2.5 построено семейство характеристик UХ’ от относительного входного сигнала β и коэффициента нагрузки α;.
Рис. 2.5
Из рисунка видно, что при R Н > > R 0 функция преобразования представляется прямой линией. С ростом коэффициента нагрузки нелинейность характеристики возрастает. Определим абсолютную погрешность нелинейности
Соответственно, относительная погрешность нелинейности определим как
В) При температуре T 0 сопротивление потенциометра равно R 0. Изменении температуры на DT = T - T 0 приводит к изменению сопротивления потенциометра:
где γ –температурный коэффициент сопротивления. В соответствии с (2.7) относительный входной сигнал β от температуры не зависит, в то время, как коэффициент нагрузки определяется как
и величина относительной погрешности с учётом изменения температуры
|

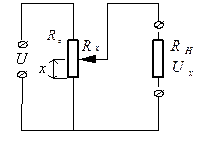
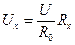 (2.2)
(2.2)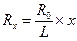 (2.3)
(2.3) (2.4)
(2.4)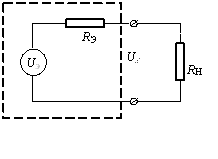
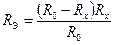 . (2.5)
. (2.5)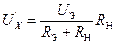 . (2.6)
. (2.6) (2.7)
(2.7)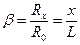 -относительный входной сигнал;
-относительный входной сигнал;  -коэффициент нагрузки.
-коэффициент нагрузки.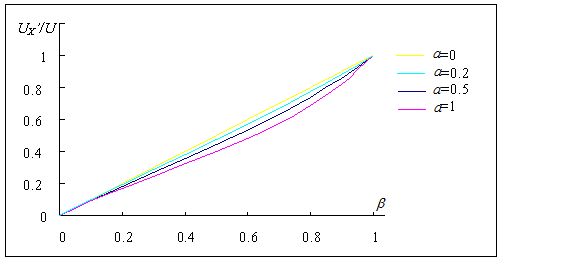
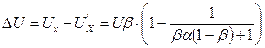 .
. .
.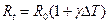 , (2.8)
, (2.8)
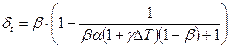 ,
, 


