Исходные данные. определение ускорения свободного падения при помощи универсального маятника
ЛАБОРАТОРНАЯ РАБОТА № 8
определение ускорения свободного падения при помощи универсального маятника
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - определить ускорение свободного падения при помощи универсального маятника.
Общие сведения
Наиболее точные измерения ускорения свободного падения выполняются с помощью косвенных методов. Многие из них основаны на использовании формул для периода колебаний математического и физического маятников. Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Период колебаний математического маятника
где l - длина маятника; g - ускорение свободного падения. Ускорение g можно вычислить, измерив Т и l. Погрешность определения g в этом случае связана с тем, что реальный маятник, используемый в лабораторных условиях, может только с некоторым приближением рассматриваться как математический (чем больше l, тем точнее измерения). Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести. Период колебаний физического маятника
где J - момент инерции маятника относительно оси качаний (точки подвеса); m - его масса; l - расстояние от центра тяжести до оси качаний. Величину L = J/ (ml) называют приведенной длиной физического маятника. Она равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Зная T, m, l и J можно по формуле (2) найти ускорение свободного падения g. Массу маятника и период его колебаний можно измерить с очень высокой точностью, но точно измерить момент инерции не удается. Указанного недостатка лишен метод оборотного маятника, который позволяет исключить момент инерции из расчетной формулы для g.
Оборотный маятник (рис.1) состоит обычно из металлического стержня А, по которому могут передвигаться и закрепляться в том или ином положении грузы В 1 и В 2 и опорные призмы С 1 и С 2. Центр масс маятника - точка О. Период колебаний маятника можно менять, перемещая грузы или опорные призмы. Маятник подвешивают вначале на призме С 1 и измеряют период его колебаний Т 1. Затем маятник подвешивают на призме С 2 и измеряют период колебаний Т 2. Допустим, что нам удалось найти такое положение грузов, при котором периоды колебаний маятников Т 1 и Т 2 около призм С 1 и С 2 совпадают, т.е.
Отсюда следует, что
По теореме Штейнера
где J 0 - момент инерции маятника относительно оси, проходящей через его центр масс и параллельной оси качаний. С учетом формул (4) и (5) можно записать
или
Тогда
и
Формула (6) аналогична формуле (1) для математического маятника. Следовательно, L = l 1 + l 2 - приведенная длина физического маятника, которая, как видно из рис.1, равна расстоянию между призмами С 1 и С 2, когда Т 1 = Т 2. Это расстояние легко может быть измерено с большой точностью. Итак, измерение ускорения свободного падения g с помощью оборотного маятника сводится к измерению периодов Т 1 и Т 2 относительно призм С 1 и С 2, достижению их равенства (с помощью перемещения призм), измерению расстояния L = l 1 + l 2 между призмами и вычислению
Чтобы пояснить процедуру достижения равенства периодов Т 1 и Т 2, исследуем, как зависит период колебаний от расстояния l между центром масс и осью качаний маятника. Согласно формулам (2) и (5), имеем
Период минимален при l min =  (рис.2). При Т > Т min одно и то же значение Т достигается при двух разных значениях l; одно из них больше, а другое меньше l min. Эти значения l 1 и l 2 и входят в формулу (1). (рис.2). При Т > Т min одно и то же значение Т достигается при двух разных значениях l; одно из них больше, а другое меньше l min. Эти значения l 1 и l 2 и входят в формулу (1).
Вначале измеряется период колебаний маятника Т 1 относительно призмы С 1. Затем маятник переворачивается и измеряется период колебаний Т 2 относительно призмы С 2. Если при этом получится Анализ точности измерения g методом оборотного маятника показывает, что погрешность измерения слабо зависит от точности, с которой выполняется равенство Т 1 = Т 2. Достаточно добиться того, чтобы периоды оказались равны друг другу с точностью 0,5 %. Кроме того, для получения достаточной точности измерения отношение l 1/ l 2 не должно быть ни слишком малым, ни слишком большим, желательно, чтобы 1,5 < l 1/ l 2 < 3.
Порядок выполнения работы
В основании 1 универсального маятника закреплена колонка 7, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 9 с фотоэлектрическим датчиком 10 (рис.3). Отвинчивая винт 5, верхний кронштейн можно поворачивать вокруг колонки. С одной стороны кронштейна 4 находится математический маятник 2, с другой - на вмонтированных вкладышах оборотный маятник 8. Длину математического маятника можно регулировать при помощи винта 3 и определять при помощи шкалы на колонке. Оборотный маятник выполнен в виде стального стержня, на котором крепятся две призмы (ножа) С 1 и С 2 и два диска 6. На стержень через 10 мм нанесены кольцевые нарезки, служащие для точного определения длины оборотного маятника (расстояние между призмами). Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки. Фотоэлектрический датчик соединен с привинченным к основанию универсальным электронным секундомером 11, который измеряет число колебаний n и общее время этих колебаний t. Период колебаний T = t / n. Последовательность проведения измерений с математическим маятником следующая:
2) отклонить маятник на угол примерно 5° и придерживать шарик рукой; 3) отпустив шарик, привести маятник в движение; 4) измерить время 10 колебаний (n=10); 5) повторить пп.1-4 еще пять раз; 6) по шкале на вертикальной колонке прибора определить длину маятника. При обработке результатов эксперимента определить период колебаний математического маятника T = t/n и вычислить ускорение свободного падения По результатам опыта составить таблицу:
Таблица 1
Средняя квадратичная ошибка для g
Записать окончательный результат в виде
Последовательность проведения опыта с оборотным маятником следующая: 1) поместить над датчиком оборотный маятник, повернув верхний кронштейн на 180°; 2) зафиксировать диски на стержне, чтобы один из них находился вблизи конца стержня, а другой вблизи его середины; 3) закрепить маятник на верхнем кронштейне на призме, находящейся вблизи конца стержня; 4) отклонить маятник примерно на 5° от положения равновесия и придерживать его рукой; 5) отпустив маятник, привести его в движение; 6) измерить время t 10 колебаний маятника; 7) определить период колебаний оборотного маятника T 1 = t / n; 8) снять маятник и закрепить его на второй призме; 9) измерить период Т 2, повторив пп.4-7; 10) сравнить периоды Т 2 и T 1; если Т 2 > T 1, вторую призму переместить в направлении диска, находящегося в конце стержня; если Т 2 < T 1, переместить ее в направлении середины стержня (положение дисков и первой призмы не менять); 11) снова измерить период Т 2 и сравнить его с величиной T 1; менять положение второй призмы до тех пор, пока значение периода Т 2 не станет равным значению периода T 1 с точностью до 0,5 %; 12) определить приведенную длину оборотного маятника L, измерив расстояние между призмами (по числу нарезок, которые нанесены через каждые 10 мм). При обработке результатов эксперимента вычислить ускорение свободного падения Средняя квадратичная ошибка
где Окончательный результат записать в виде
Контрольные вопросы
1. Что такое математический маятник? 2. Что такое физический маятник? 3. Почему с помощью маятников можно измерить ускорение свободного падения? 4. С чем связана погрешность определения g с помощью математического маятника? 5. С чем связана погрешность определения g с помощью физического маятника и как ее устранить? 6. В чем заключается метод оборотного маятника?
Исходные данные Задан контактор переменного тока типа КМИ из Каталога электротехнической продукции компании IEK, Коммутационное оборудование, 2008г., Интернет-сайт - www.iek.ru
*время искусственно увеличено в 5 раз в учебных целях, фактическое время срабатывания не превышает 22-35 мС. Время от момента включения цепи втягивающей катушки до момента первоначального касания силовых (главных) контактов называется собственным временем включения контактора. Время от момента снятия напряжения с втягивающей катушки до момента появления зазора между главными контактами называется собственным временем отключения магнитного пускателя.
|

 , (1)
, (1) , (2)
, (2)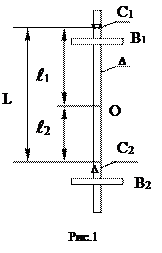 Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника.
Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника.
 .
.  (3)
(3)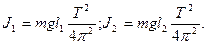 (4)
(4) (5)
(5)
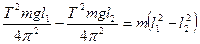 .
.

 . (6)
. (6) (7)
(7)

 , то этому будет соответствовать
, то этому будет соответствовать  . И для того, чтобы приблизить
. И для того, чтобы приблизить  и Т 1, надо увеличить
и Т 1, надо увеличить  . Для этого надо призму С 2 передвинуть от середины стержня к краю. Если получится
. Для этого надо призму С 2 передвинуть от середины стержня к краю. Если получится  1) поместить над датчиком математический маятник, повернув соответствующим образом верхний кронштейн;
1) поместить над датчиком математический маятник, повернув соответствующим образом верхний кронштейн; для каждого измерения и среднее
для каждого измерения и среднее 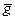 .
.
 .
.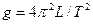 при Т = Т 1 = Т 2 и среднюю квадратичную ошибку
при Т = Т 1 = Т 2 и среднюю квадратичную ошибку  , где
, где  - погрешность измерения времени, оцениваемая исходя из точности прибора.
- погрешность измерения времени, оцениваемая исходя из точности прибора.
 - погрешность измерения длины, оцениваемая по цене деления измерительной линейки.
- погрешность измерения длины, оцениваемая по цене деления измерительной линейки. .
.


