КРАТКАЯ ТЕОРИЯ
где Получили уравнение гармонических колебаний:
где циклическая частота колебаний маятника – число колебаний за Рассмотрим теперь два маятника, связанные пружиной жесткостью
Маятники могут колебаться в произвольных плоскостях, в частности, как в плоскости чертежа, так и перпендикулярно к ней. Среди всевозможных видов колебаний связанных маятников ради простоты рассмотрим колебания только в плоскости чертежа. Рассмотрим случай возбуждения колебаний путем первоначального отклонения маятников от положения равновесия и при этом только на одинаковый угол. Очевидно, что здесь возможны два варианта: отклонения синфазны, т.е. в одну сторону, как показано на рис.3, и отклонения противофазны, т.е. в противоположные стороны, как показано на рис.4.
Рассмотрим вначале первый случай, изображенный на рис.3. Так как маятники отклонены на одинаковый угол, то пружина не будет испытывать деформации и, следовательно, не будет оказывать силового воздействия на маятники. Эта ситуация сохранится и во все последующие моменты времени, так как периоды колебаний маятников одинаковы, т.е.:
Таким образом, связанные маятники будут совершать гармонические колебания с частотой
Рассмотрим теперь случай, изображенный на рис. 4. Ясно, что колебания маятников будут также идентичны друг другу, но в противофазе, т.е.:
Поэтому рассмотрим колебания одного только маятника. На маятник в дополнение к силе тяжести будет действовать еще сила упругости
Двойка появляется потому, что при линейном смещении маятника на величину
и направленный в ту же сторону, что и момент силы тяжести. Следовательно, уравнение (1) примет вид:
В приближении малых углов уравнение (7) примет вид:
Получим уравнение гармонических колебаний:
где
циклическая частота таких колебаний. Следовательно, связанные маятники могут совершать колебания с частотами:
В общем случае произвольного способа возбуждения колебаний каждый из маятников осуществляет сложное колебание, характер которого удобно наблюдать при слабой связи между маятниками. В этом случае разность
Таким образом, в системе двух связанных маятников в зависимости от способа возбуждения возможны следующие виды колебаний: 1. Оба маятника отклонили в одну сторону на одинаковый угол и отпустили. При этом возникает колебание 1 с частотой, определяемой по формуле (5). 2. Оба маятника отклонили в разные стороны на одинаковый угол и отпустили. При этом возникает колебание 2 с частотой, определяемой по формуле (9). 3. Один маятник удерживаем в положении равновесия, второй отклоняем на некоторый угол, после чего оба маятника отпускаем. При этом возникают биения, определяемые суперпозиций колебаний 1 и 2, с частотой, определяемой по формуле (10).
Отметим, что возможны и другие способы возбуждения колебаний, соответственно, и другой их характер.
|



 , (1)
, (1) – масса маятника,
– масса маятника, 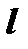 –его длина,
–его длина,  – угол отклонения.
– угол отклонения.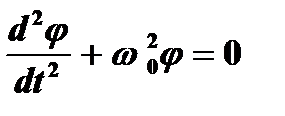 ,(2)
,(2) (3)
(3) секунды. Эта частота называется собственной частотой колебаний маятника, а само колебание с этой частотой – нормальным колебанием или гармоникой.
секунды. Эта частота называется собственной частотой колебаний маятника, а само колебание с этой частотой – нормальным колебанием или гармоникой. так, как показано на рис. 2.
так, как показано на рис. 2.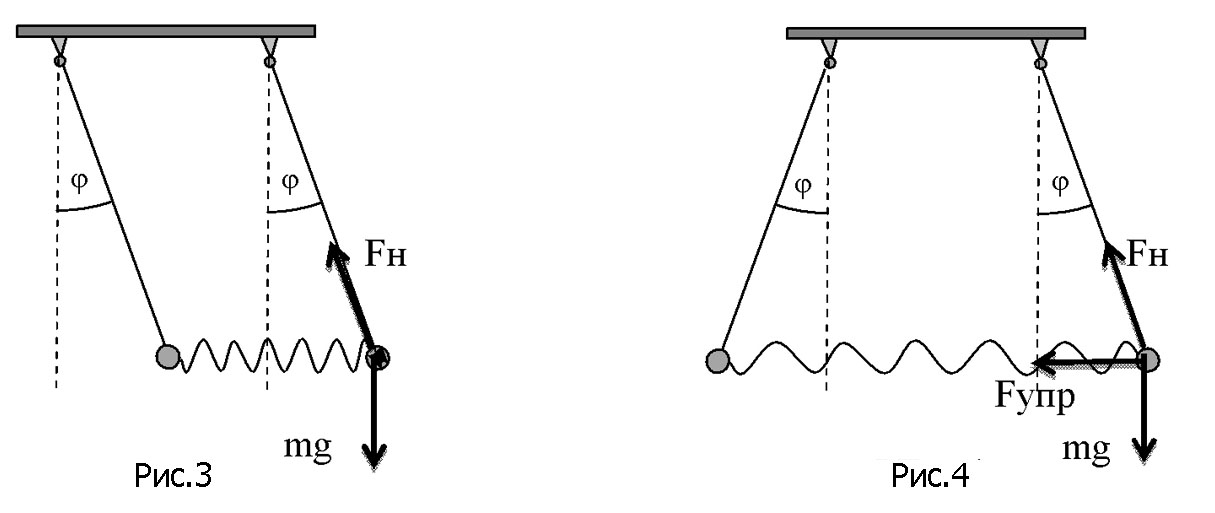
 . (4)
. (4) , равной частоте
, равной частоте  :
: .(5)
.(5) .(6)
.(6) со стороны деформированной пружины, которая согласно закону Гука, будет равна по модулю:
со стороны деформированной пружины, которая согласно закону Гука, будет равна по модулю: .
. , пружина деформируется на удвоенное такое же расстояние. Эта сила упругости создаст момент силы
, пружина деформируется на удвоенное такое же расстояние. Эта сила упругости создаст момент силы  , равный
, равный
 . (7)
. (7) .
. , (8)
, (8) (9)
(9)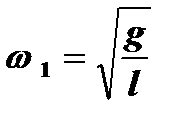 или
или 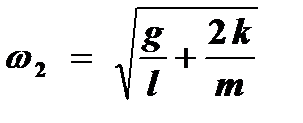 .
. мала по сравнению с нормальными частотами и, при сложении гармонических колебаний с близкими частотами, возникают биения – колебания с периодически изменяющейся (пульсирующей) амплитудой. Частота биений:
мала по сравнению с нормальными частотами и, при сложении гармонических колебаний с близкими частотами, возникают биения – колебания с периодически изменяющейся (пульсирующей) амплитудой. Частота биений: . (10)
. (10)


