Методические указания к решению задачи.
· Навыки работы с компьютером,оргтехникой. · Английский-базовый. · · Личные качества · Коммуникабельность, внимательность. · Умение находить общий язык с клиентами. · Стрессоустойчивость. · Стремление к развитию и профессиональному росту. · Быстрая обучаемость, ответственность
Лабораторная работа № 4 Задача. Электроснабжение n цехов промышленного предприятия выполнено по радиальной схеме от шин U = 10 кВ ГПП (рисунок 4.1). Заданы реактивные нагрузки цехов Qi и активные сопротивления радиальных линий Ri (i = 1, 2,... n). Требуется оптимально распределить заданную суммарную мощность компенсирующих устройств Qk между цехами. Критерий оптимальности – минимум суммарных потерь активной мощности в линиях. Исходные данные для решения задачи приведены в таблице 4.1.
Рисунок 4.1
Таблица 4.1
Методические указания к решению задачи.
Суммарные потери активной мощности в радиальной схеме от реактивных нагрузок Qi при установке у каждой нагрузки компенсирующего устройства мощностью Qki определяются выражением:
Минимум функции ∆Р ищется при ограничении:
Следуя методу Лагранжа, вместо минимума функции (4.1) при ограничении (4.2) будем искать минимум функции Лагранжа, которая записывается в виде:
где λ – неопределенный множитель Лагранжа. Из курса высшей математики известно, что в точке минимума нелинейной функции ее частные производные по всем переменным равны нулю, т.е.:
Решение системы линейных уравнений (4.4) даст искомые значения переменных Qki. Суммарные потери активной мощности в электрической сети рассчитываются по выражению (4.1).
|


 (4.1)
(4.1)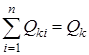 или
или  (4.2)
(4.2) . (4.3)
. (4.3) (4.4)
(4.4)


