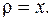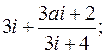II. Варианты заданий
1. Произведя деление, записать в алгебраической форме.
2. Записать в тригонометрической и показательной форме.
3..
4. Вычислить интеграл от аналитической функции.
5. Вычислить интеграл вдоль кривой  .
.
6. Вычислить по интегральной формуле Коши или с помощью вычетов.
7..
Вариант № 1
1. 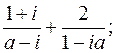
2. 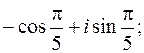
3. 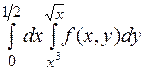
4. 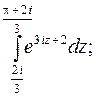
5.  от 1 до
от 1 до 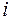 ;
;
6.  , где
, где  окружность радиуса 3 с центром в начале координат.
окружность радиуса 3 с центром в начале координат.
7. Найти длину кардиоиды 
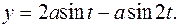
Вариант № 2
1. 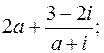
2. 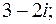
3. 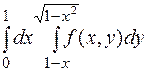
4. 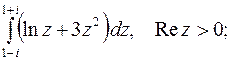
5.  от -2
от -2 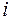 до 2;
до 2;
6.  , где
, где  контур, содержащий точку
контур, содержащий точку  внутри;
внутри;
7. Вычислить координаты центра тяжести однородной дуги астроиды  расположенной в I квадранте.
расположенной в I квадранте.
Вариант № 3
1. 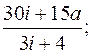
2. 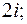
3. 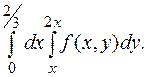
4. 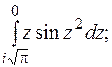
5.  отрезок
отрезок  от
от 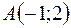 до
до 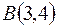 ;
;
6.  , где
, где 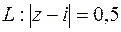 ;
;
7. Найти массу дуги окружности  расположенной в I квадранте, если плотность распределения массы в каждой точке кривой равна квадрату ординаты.
расположенной в I квадранте, если плотность распределения массы в каждой точке кривой равна квадрату ординаты.
Вариант № 4
1. 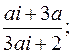
2. 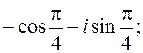
3. 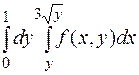
4. 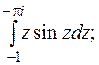
5. 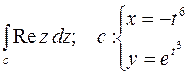 от
от 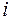 до
до  ;
;
6.  , где
, где  окружность
окружность  ;
;
7. Вычислить статический момент относительно плоскости  одного витка винтовой линии
одного витка винтовой линии 
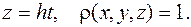
Вариант № 5
1. 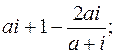
2. 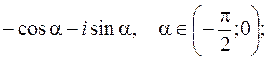
3. 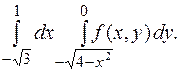
4. 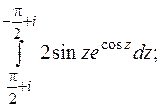
5.  от
от  до 1;
до 1;
6.  ;
;
Вычислить момент инерции относительно точки  дуги окружности
дуги окружности 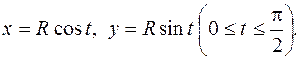
Вариант № 6
1. 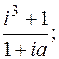
2. 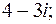
3. 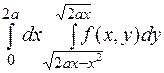
4. 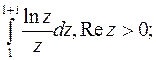
5. 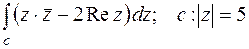 от 5
от 5 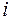 до –5
до –5 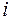 ;
;
6.  , где
, где 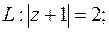
7. Вычислить статический момент относительно оси  верхней половины эллипса
верхней половины эллипса 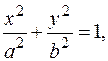 если плотность распределения массы в точке равна ординате этой точки.
если плотность распределения массы в точке равна ординате этой точки.
Вариант № 7
1. 
2. 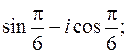
3. 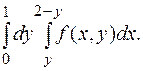
4. 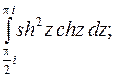
5.  от 1+2
от 1+2 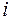 до 0;
до 0;
6.  ;
;
7. Вычислить массу отрезка  , если
, если 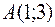 и
и  а плотность распределения массы в каждой точке
а плотность распределения массы в каждой точке  равна
равна 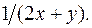
Вариант № 8
1. 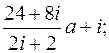
2. 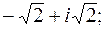
3. 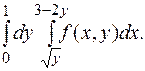
4. 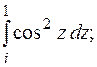
5.  отрезок
отрезок  от
от  до
до 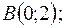
6. 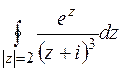 ;
;
7. Найти массу первого витка винтовой линии 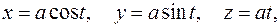 если плотность распределения массы в каждой точке
если плотность распределения массы в каждой точке 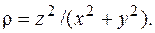
Вариант № 9
1. 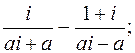
2. 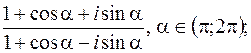
3. 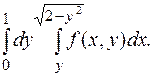
4. 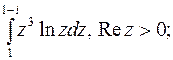
5.  от 0 до 1+
от 0 до 1+ 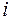 ;
;
6. 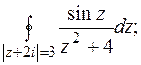
7. Найти массу одного витка однородной винтовой линии 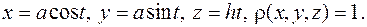
Вариант № 10
1. 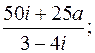
2. 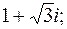
3. 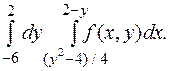
4. 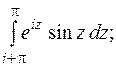
5.  от (3;0) до (0;2);
от (3;0) до (0;2);
6.  ;
;
7. Вычислить массу участка цепной линии 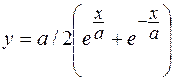 между точками с абсциссами
между точками с абсциссами  и
и  , если плотность распределения массы в каждой точке обратно пропорциональна ординате точки, причем в точке
, если плотность распределения массы в каждой точке обратно пропорциональна ординате точки, причем в точке  плотность равна
плотность равна  .
.
Вариант № 11
1. 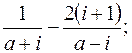
2. 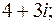
3. 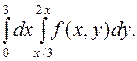
4.  ;
;
5. 
 от
от  до
до 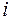 ;
;
6.  ;
;
7. Найти статический момент относительно оси  дуги кривой
дуги кривой  от
от  до
до  , если ее плотность
, если ее плотность 
Вариант № 12
1. 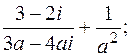
2. 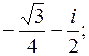
3. 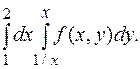
4. 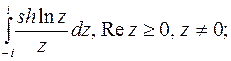
5. 
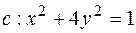 от
от  до 1;
до 1;
6. 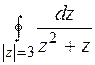 ;
;
7. Вычислить момент инерции относительно начала координат четверти окружности,  расположенной в первом квадранте, если плотность распределения массы
расположенной в первом квадранте, если плотность распределения массы 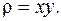
Вариант № 13
1. 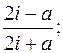
2.  ;
;
3. 
4.  ;
;
5. 
 отрезок, соединяющий
отрезок, соединяющий  и
и  ;
;
6.  ;
;
7. Найти массу развертки окружности 

 , если плотность распределения массы в точке равна расстоянию этой точки до начала координат.
, если плотность распределения массы в точке равна расстоянию этой точки до начала координат.
Вариант № 14
1. 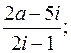
2.  ;
;
3. 
4.  ;
;
5. 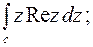

 от –1 до
от –1 до  ;
;
6. 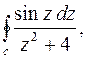 где
где  окружность
окружность  ;
;
7. Найти массу кардиоиды 
 , если плотность распределения массы в каждой точке равна ординате этой точки.
, если плотность распределения массы в каждой точке равна ординате этой точки.
Вариант № 15
1. 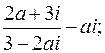
2. 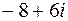 ;
;
3. 
4. 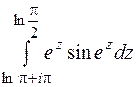 ;
;
5.  ;
; 
 от –3 до
от –3 до 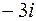 ;
;
6. 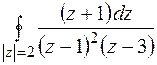 ;
;
7. Найти массу кардиоиды 
 , если плотность распределения массы в каждой точке равна ординате этой точки.
, если плотность распределения массы в каждой точке равна ординате этой точки.
Вариант № 16
1. 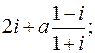
2.  ;
;
3. 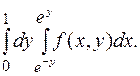
4.  ;
;
5.  ;
; 
 от 0 до
от 0 до  ;
;
6.  ;
;
7. Найти статический момент относительно оси  дуги эллипса
дуги эллипса  если ее плотность
если ее плотность 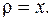
Вариант № 17
1. 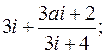
2. ![]()

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Задержки и неисправности пистолета Макарова 1.Что может произойти при стрельбе из пистолета, если загрязнятся пазы на рамке...
Вопрос. Отличие деятельности человека от поведения животных главные отличия деятельности человека от активности животных сводятся к следующему: 1...
Расчет концентрации титрованных растворов с помощью поправочного коэффициента При выполнении серийных анализов ГОСТ или ведомственная инструкция обычно предусматривают применение раствора заданной концентрации или заданного титра...
|
Концептуальные модели труда учителя В отечественной литературе существует несколько подходов к пониманию профессиональной деятельности учителя, которые, дополняя друг друга, расширяют психологическое представление об эффективности профессионального труда учителя...
Конституционно-правовые нормы, их особенности и виды Характеристика отрасли права немыслима без уяснения особенностей составляющих ее норм...
Толкование Конституции Российской Федерации: виды, способы, юридическое значение Толкование права – это специальный вид юридической деятельности по раскрытию смыслового содержания правовых норм, необходимый в процессе как законотворчества, так и реализации права...
|

 .
.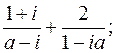
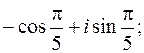
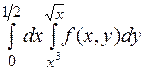
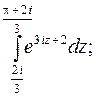
 от 1 до
от 1 до 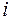 ;
; , где
, где  окружность радиуса 3 с центром в начале координат.
окружность радиуса 3 с центром в начале координат.
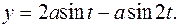
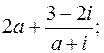
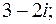
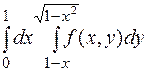
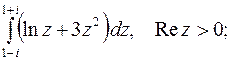
 от -2
от -2  , где
, где  внутри;
внутри; расположенной в I квадранте.
расположенной в I квадранте.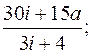
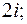
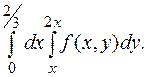
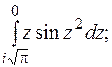
 отрезок
отрезок  от
от 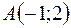 до
до 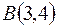 ;
; , где
, где 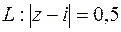 ;
; расположенной в I квадранте, если плотность распределения массы в каждой точке кривой равна квадрату ординаты.
расположенной в I квадранте, если плотность распределения массы в каждой точке кривой равна квадрату ординаты.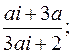
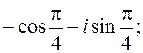
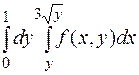
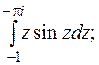
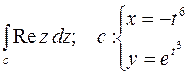 от
от  ;
; , где
, где  ;
; одного витка винтовой линии
одного витка винтовой линии 
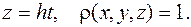
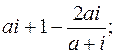
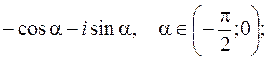
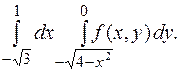
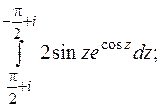
 от
от  до 1;
до 1; ;
; дуги окружности
дуги окружности 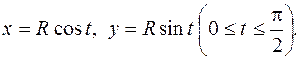
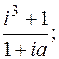
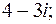
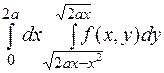
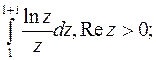
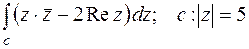 от 5
от 5  , где
, где 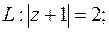
 верхней половины эллипса
верхней половины эллипса 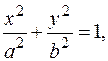 если плотность распределения массы в точке равна ординате этой точки.
если плотность распределения массы в точке равна ординате этой точки.
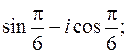
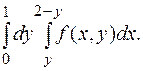
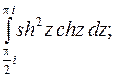
 от 1+2
от 1+2  ;
;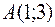 и
и  а плотность распределения массы в каждой точке
а плотность распределения массы в каждой точке  равна
равна 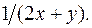
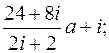
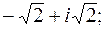
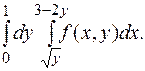
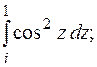
 отрезок
отрезок  до
до 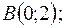
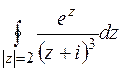 ;
;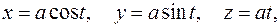 если плотность распределения массы в каждой точке
если плотность распределения массы в каждой точке 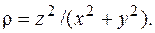
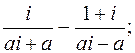
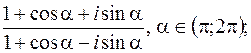
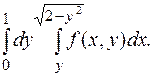
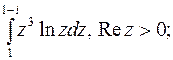
 от 0 до 1+
от 0 до 1+ 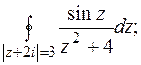
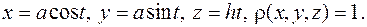
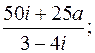
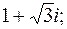
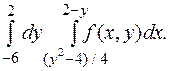
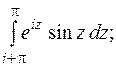
 от (3;0) до (0;2);
от (3;0) до (0;2); ;
;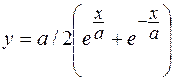 между точками с абсциссами
между точками с абсциссами  и
и  , если плотность распределения массы в каждой точке обратно пропорциональна ординате точки, причем в точке
, если плотность распределения массы в каждой точке обратно пропорциональна ординате точки, причем в точке  плотность равна
плотность равна  .
.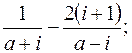
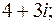
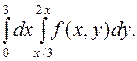
 ;
;
 от
от  до
до  ;
; дуги кривой
дуги кривой  от
от  до
до  , если ее плотность
, если ее плотность 
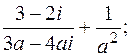
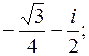
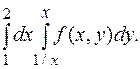
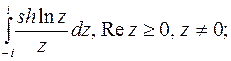

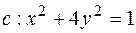 от
от  до 1;
до 1;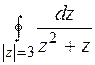 ;
; расположенной в первом квадранте, если плотность распределения массы
расположенной в первом квадранте, если плотность распределения массы 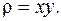
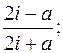
 ;
;
 ;
;
 отрезок, соединяющий
отрезок, соединяющий  и
и  ;
; ;
;

 , если плотность распределения массы в точке равна расстоянию этой точки до начала координат.
, если плотность распределения массы в точке равна расстоянию этой точки до начала координат.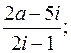
 ;
;
 ;
;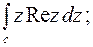
 от –1 до
от –1 до 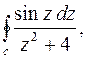 где
где  ;
;
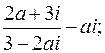
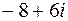 ;
;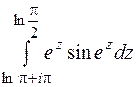 ;
; ;
;  от –3 до
от –3 до 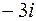 ;
;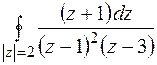 ;
; , если плотность распределения массы в каждой точке равна ординате этой точки.
, если плотность распределения массы в каждой точке равна ординате этой точки.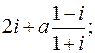
 ;
;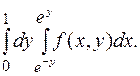
 ;
; ;
;  от 0 до
от 0 до  ;
; ;
; если ее плотность
если ее плотность