МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
8. Выведите формулу (5). ОПРЕДЕЛЕНИЕ РАЗМЕРОВ МОЛЕКУЛЫ ОЛЕИНОВОЙ КИСЛОТЫ
Цель работы: 1. Изучить метод определения размеров молекулы олеиновой кислоты при растекании раствора на поверхности воды. 2. Определить эффективный диаметр и длину молекулы олеиновой кислоты. Литература: 1. Д.В.Сивухин. Общий курс физики. Термодинамика и молекулярная физика. М., Наука, 1979, с.332-335, 426-429 2. А.Н.Матвеев. Молекулярная физика. М., Высшая школа, 1981, с.278-285. 3. И.В.Савельев. Курс общей физики. том.1. М., Наука, 1987 с.371-382.
ТЕОРИЯ
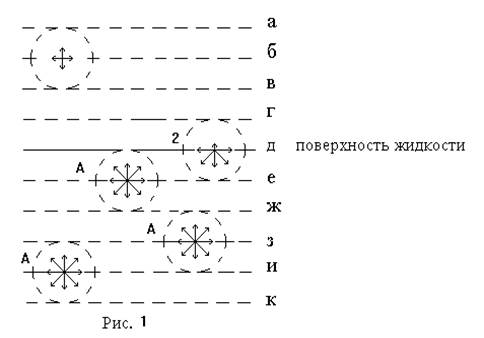
Внутреннее строение жидкостей сложнее строения газов. Во-первых, мы считаем в газах молекулы свободными, движущимися независимо друг от друга, если только не считать их случайных столкновений между собой. В жидкостях молекулы настолько сближены, что столкновения между ними должны происходить несравненно чаще, чем в газах. Вследствие этого каждая молекула должна двигаться около некоторого среднего своего положения, меняющегося сравнительно медленно, т.е. постепенное перемещение молекул с одного места на другое в жидкостях происходит в течение большего промежутка времени, чем в газах. Во-вторых, поскольку межмолекулярные промежутки в жидкостях невелики, то пренебрегать силами взаимодействия молекул нельзя. Эти силы называют силами сцепления и их величина уменьшается в зависимости от расстояния значительно быстрее, чем у силы гравитационного взаимодействия. Конечно, силы сцепления имеются и в газах, но они весьма малы и поэтому большой роли не играют. В жидкостях же, наоборот, наличие этих сил постоянно обнаруживается во множестве разнообразных явлений и притом в особенности вблизи их поверхности. Когда молекула А (рис.1) находится внутри жидкости, то она со всех сторон окружена такими же молекулами, действующими на нее с силами сцепления, радиус действия которых ограничен расстоянием, обозначим его R. На эту молекулу практически не действуют те молекулы, которые находятся в н е сферы радиуса R, а силы взаимодействия внутренних молекул (по причине их симметричного и равномерного расположения) на молекулу А компенсируются. На рис 1. изображены плоскости а,б,в,г,д,е,ж,з,и,к - расстояния между которыми равны радиусу сферы частичного взаимодействия молекул R.
Когда молекула 2 находится на поверхности (воображаемой) жидкости, то равномерность распределения молекул внутри сферы частичного взаимодействия нарушается (вне жидкости - газ, и число молекул в единице объема в миллионы раз меньше, чем в жидкости) и равнодействующая сил сцепления направлена внутрь жидкости перпендикулярно ее поверхности, молекула как бы втягивается внутрь жидкости силой, удерживающей ее от вылета из жидкости. Это относится не только ко всем молекулам, находящимся у поверхности жидкости, но и к тем, которые находятся внутри жидкости на расстоянии от ее поверхности, меньшем радиуса R. Плоскость "е" является нижней границей поверхностной пленки, частицы которой подвержены действию сил, направленных внутрь жидкости. Вся эта пленка оказывает давление на жидкость, которое похоже на давление надутого резинового шарика на находящийся в нем воздух. Однако такое сравнение верно только внешне. Различие состоит в том, что при увеличении площади поверхности резиновой пленки увеличивается расстояние между молекулами и сама длина молекул (они "тянутся"), при растяжении же поверхности жидкости увеличивается число ее молекул в единице площади, т.е. в "пустые" места перемещаются молекулы из глубин жидкости. Математически это выражается в том, что сила натяжения резины, по сути сила упругости, в соответствии с законом Гука зависит от величины деформации и при равенстве сил упругости и внешней силы, вызвавшей деформацию, наступает состояние равновесия (шар больше не увеличивается в объеме). В случае же поверхностного натяжения величина натяжения не зависит от площади поверхности пленки, по крайней мере до тех пор, пока толщина пленки не становится весьма малой (как показывают измерения - порядка 5·10- 4 м). Fпов = s·l,
где s- некоторая постоянная величина, характеризующая вещество пленки (она называется поверхностным натяжением); l - длина линии, перпендикулярно которой действует сила поверхностного натяжения.
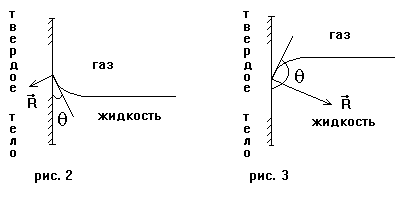
На рис.2 изображена поверхность жидкости у края капилляра (твердое тело) в случае смачивающей жидкости, а на рис.3 - несмачивающая жидкость. Сила R-равнодействующая всех сил, действующих на элемент (частицу) жидкости, q-краевой угол. В случае смачивающей жидкости силы сцепления молекул жидкости с молекулами твердого тела больше, чем между молекулами жидкости. Сила R всегда направлена перпендикулярно касательной к поверхности жидкости, т.к. только при этом условии поверхность жидкости будет в покое.
На рис.4 представлена в сечении часть капли смачивающей жидкости на поверхности твердого тела (трехфазная система).Форма капли определяется влиянием сил взаимодействия молекул трех сред: газа (1), жидкости (2) и твердого тела (3).
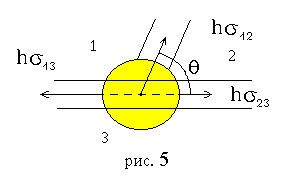
Эти три среды имеют общую границу (рис.5), внутри которой содержится элемент m вещества (заштрихованный диск). На внешнюю поверхность диска кроме обычного давления, одинакового со всех сторон, действуют еще силы поверхностного натяжения h·s13, h·s12, h·s23, где h длина дуги окружности диска,расположенной внутри каждой поверхностной пленки. Эти силы будут направлены перпендикулярно к отдельным элементам окружности и по касательным к соответствующим поверхностям раздела. Обозначим через q угол между поверхностью жидкость – газ и поверхностью твердого тела. Одним из условий равновесия диска является равенство нулю векторной суммы действующих на него сил. В случае, когда можно пренебречь силой тяжести по сравнению с силами поверхностного натяжения, имеем: s12·cosq - s13 + s23 = 0, откуда: s23 - s13
s12
Так как s12, s13, s23 постоянны, а cosq не может быть больше 1, то в случае равновесия имеет место условие
s23 - s13 -------------- = < 1. s12
Угол q, определяемый равенством (1), называют краевым углом. Каждая комбинация твердого, жидкого и газообразного тела характеризуется определенным краевым углом. Если
s23 - s13 > 0,
то угол q острый. В этом случае говорят, что имеет место частичное смачивание. Если s23 - s13 < 0,
то cos q > 0 и угол q - тупой, имеет место частичное несмачивание. Примерами полного смачивания являются соприкосновение со стеклом этилового и метилового спиртов и бензина. Частично смачивают стекло, например, эфир (q = 160) и керосин (q = 260). Многие органические жидкости (эфир, скипидар, керосин) растекаются по поверхности воды, т.е. имеет место полное смачивание. Для некоторых жидкостей (бензол, жирные кислоты, масло) явление максимального растекания наблюдается только для первых капель, помещенных на поверхность чистой воды. Это объясняется загрязнением поверхности воды первыми каплями при их растекании и как следствие этого - уменьшением поверхностного натяжения настолько, что равновесие капель становится возможным. Если площадь поверхности воды достаточно велика, то может образоваться мономолекулярный слой, т.е. слой толщиной в одну молекулу. Расположение таких молекул на поверхности воды показано на рис.6.
В настоящей работе для определения размеров молекул олеиновой кислоты используется метод, предложенный Ленгмюром и Дево. Для измерений используется кювета 60 см Х 40 см. Когда капля раствора олеиновой кислоты в легколетучей жидкости (спирте) падает на поверхность воды, то растворитель быстро испаряется, а олеиновая кислота растекаясь, образует на поверхности воды мономолекулярный слой (при достаточной для этого поверхности чистой воды). Если поверхность воды посыпать предварительно тонким слоем пробковых опилок или талька, то на ней образуется свободное от порошка округлое пятно. По диаметру этого пятна можно приближенно рассчитать площадь поперечного сечения одной молекулы олеиновой кислоты. Если в капле раствора содержится n молекул олеиновой кислоты, каждая с площадью поперечного сечения Sm, то
Sm·n = S (2),
где S - площадь круга, образованного растекшейся олеиновой кислотой на поверхности воды. Из (2) имеем:
Число молекул олеиновой кислоты n в капле можно найти, если известны масса m олеиновой кислоты, содержащаяся в капле раствора, и ее молярная масса М:
n = m·Na/M (4),
где Na - число Авогадро. Тогда эффективный диаметр одной молекулы d находим по формуле:
Длину h молекулы олеиновой кислоты грубо можно оценить, руководствуясь следующими соображениями:
h = V/S (6),
где V - объем мономолекулярного слоя, S - площадь его поверхности (площадь круга, диаметр которого Dср).
V = m/r
где m - масса олеиновой кислоты в капле раствора, r - плотность олеиновой кислоты. Подставив выражения S и V в (6), получим:
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ 1.Наполняют кювету водой и посыпают успокоившуюся ее поверхность пробковым порошком или тальком (слой порошка на поверхности воды должен быть тонким, равномерным), оставляя в центре кюветы небольшую площадь чистой воды. 2. С помощью пипетки с высоты 2-3 мм капают одну каплю раствора в середину поверхности воды в кювете. 3. Когда капля перестает растекаться, линейкой измеряют значения двух взаимно перпендикулярных диаметров D1 и D2 образовавшейся фигуры. 4. Опыт проделывают еще два раза, тщательно промывая кювету после каждого опыта. 5. Определяют на аналитических весах массу m1 пустого сосуда (бюкса) для сбора капель олеиновой кислоты. 6. Затем, накапав в бюкс 20 капель 0,3-процентного раствора олеиновой кислоты, определяют на аналитических весах массу m2 бюкса вместе с раствором. 7. Результаты измерений и вычислений записывают в таблицу.
|

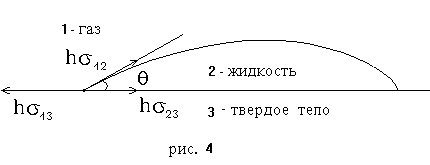
 cosq = --------------- (1).
cosq = --------------- (1).
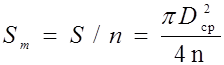 (3).
(3).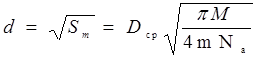 (5).
(5).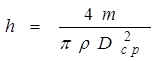 (7)
(7)


