Задания расчетно-графической работы по математике
Согласно закону полного тока намагничивающая сила катушки равна сумме магнитных напряжений на всех участках замкнутого контура:
где
контуре стали;
6. Вычисление параметров катушки по заданным виткам: - по намагничивающей силе определяем ток катушки
-вычисляем напряжение в катушке где - диаметр провода обмотки определяем через плотность тока
- вычисляем мощность катушки - температуру перегрева катушки определяем по приближённой формуле S – наружная поверхность обмотки и магнитопровода (охлаждаемой части), определяемая по рисунку 13д:
Если окружающая температура tокр=20°С, то катушка будет нагреваться до температуры: 7. Пересчёт катушки на заданное напряжение сети Uс. При изменении напряжения питания катушки контактора с расчётного значения Uк на заданное напряжение Uс следует в тех же габаритах намотать катушку другим проводом и с другим числом витков, сохранив при этом: - число ампер-витков IкWк=IсWс, т.е. намагничивающую силу; - мощность катушки UкIк=UсIс, - плотность тока в проводе обмотки jк, jс или Из этих трех условий находим: - ток катушки Iк при питании ее от сети постоянного напряжения Uс,

- диаметр провода для намотки новой катушки: -число витков новой катушки: Согласно общему принципу конструирования контакторов тяговая характеристика должна проходить выше его механической характеристики. Поэтому положим, что во включенном положении общая сила тяги электромагнита F на 20% больше требуемой силы для нажатия всех контактов F1, откуда F1=F/1,2. Усилие F2 на контактной группе пересчитываем с учетом рычажной передачи (рис. I3a-г), для чего составляем уравнение моментов вращающихся рычагов относительно оси поворота, например, для рис. I3б:
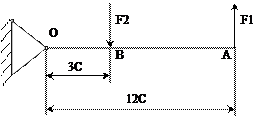
На каждый из двух контактов приходится половина этой силы, т.к. в группе всего 2 контакта, откуда сила прижатия одного контакта равна:
По силе нажатия вычисляем переходное сопротивление контакта, которое для одноточечного контакта равно:
где ε = 10‾³ для меди. Вычисляем номинальный ток IН нагрузки, протекающий через контакты по мощности нагрузки РН и напряжению сети UС:
Определяем падение напряжения на сопротивлении контактного перехода:
За счет потерь электроэнергии на переходном сопротивлении контакт нагревается: где
9. Вычислим электродинамическую силу отбрасывания контакта при прохождении тока короткого замыкания: Fэ=-10-7I где Iкз=10In - ток короткого замыкания, S и S0 – площадь всего контакта и контактирующей поверхности. Положим для простоты S/S0=10
Fэ<Fк, то контакты не разомкнутся при КЗ и не будут подгорать от возникшей в зазоре дуги.
Используемая литература 1. Чунихин А.А. Электрические аппараты. –М.:Энергоатомиздат, 1988. 2. Родштейн Л.А. Электрические аппараты. –Л.:Энергоатомиздат, 1989. 3. Электрические аппараты высокого напряжения. Под ред. Г.Н. Александрова. –Л.:Энергоатомиздат, 1989. 4. Буль Б.К., Буткевич Г.В. и др. Основы теории электрических аппаратов. –М.: Высшая школа, 1970. 5. Таев И.С. Электрические аппараты. М.: Энергия, 1977. Филинов В.А. Тензорно-аналитические методы расчета несимметричных режимов в трехфазных системах электроснабжения. МУ. Тверь: ТГТУ, 2000
Задания расчетно-графической работы по математике
|



 – напряжённость магнитного поля в стали, которую определяем по кривой намагничивания стали для расчётного значения магнитной индукции;
– напряжённость магнитного поля в стали, которую определяем по кривой намагничивания стали для расчётного значения магнитной индукции; -длина средней силовой линии в одном
-длина средней силовой линии в одном -напряжённость магнитного поля в зазорах;
-напряжённость магнитного поля в зазорах; - суммарная длина зазоров.
- суммарная длина зазоров.


 средняя длина витка катушки;
средняя длина витка катушки; ,причём
,причём ,откуда
,откуда


 , где
, где 


 .
.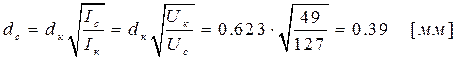
 8. Вычисление параметров силовых контактов.
8. Вычисление параметров силовых контактов.
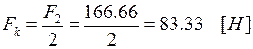

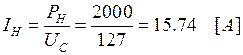
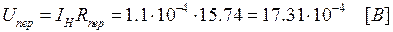
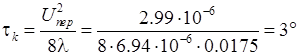
 - перегрев контакта по сравнению с окружающей температурой,
- перегрев контакта по сравнению с окружающей температурой, для меди.
для меди. ln S/S0,
ln S/S0,





