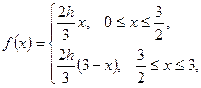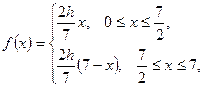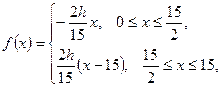ОБЩИЕ ПОЛОЖЕНИЯ. I. Исследовать сходимость рядов.
I. Исследовать сходимость рядов. 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) II. Найти область сходимости ряда. 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) III. Разложить функцию в ряд Тейлора по степеням 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) IV. Вычислить определенный интеграл с точностью 1. 6. V. Разложить в ряд Фурье функцию с периодом Т. 1. 3. 5. 7. 9. V. Выяснить, дифференцируема ли функция. В случае дифференцируемости найти производную. 1. 5. 9. VI. Найти. 1. 5. 9. VII. Вычислить 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. VIII. Решить методами операционного исчисления: 1. а) 2. а) 3. а) 4. а) 5. а) 6. а) б) 7. а) б) 8. а) б) 9. а) 10. а) б) IX. Решить уравнение колебания струны методом Фурье. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
РЕГЛАМЕНТ ЗАКРЫТИЕ ЛЕТНЕГО СЕЗОНА По картингу 2015 года (Организованно в соответствии со Спортивным Кодексом РАФ) Место проведения: Санкт-Петербург, Колпино, картодром СПб ГБУ СОК «Ижорец» Срок проведения: 25 октября 2015 г. ОБЩИЕ ПОЛОЖЕНИЯ 1.1. Соревнование «ЗАКРЫТИЕ ЛЕТНЕГО СЕЗОНА по картингу 2015 года» не является классифицируемым соревнованием и проходит по регламенту Учебно-тренировочных сборов. 1.2. Состав соревнования: Соревнование проводится в классах: Микро Parilla, Ротакс Макс, Ротакс Юниор, 1660061811Я, Ротакс Мини, Ротакс Микро, Мини, 1660131511Н, Супер Мини, 1660031811Н, Ракет 85, 1660141811Н, Ракет 120, Национальный Юниор, Национальный, 1660151511Я, KF (KF2), KFj (KF3), 166161511Я, KZ-2, 1660181511Л. 1.3. Нормативными документами данных соревнований являются: - Единая Всероссийская спортивная классификация (ЕВСК); - Всероссийский реестр видов спорта (ВРВС); - Спортивный Кодекс РАФ» (СК РАФ); - Общие условия проведения Чемпионатов, Первенств и Кубков России (ОУ РАФ); - Национальные спортивные правила по картингу АК РАФ (СП АК РАФ); - Классификация и Технические Требования к автомобилям «карт» (КиТТ); - Регламент Официальных соревнований России по картингу (Чемпионатов, Первенств и Кубков России). - Настоящий Регламент.
|

 , б)
, б)  , в)
, в) 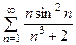 , г)
, г)  .
. , б)
, б)  , в)
, в)  , г)
, г)  .
.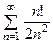 , б)
, б)  , в)
, в)  , г)
, г) 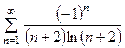 .
.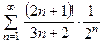 , б)
, б)  , в)
, в)  , г)
, г)  .
.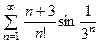 , б)
, б)  , в)
, в)  , г)
, г)  .
.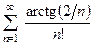 , б)
, б) 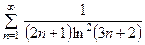 , в)
, в)  , г)
, г)  .
. , б)
, б)  , в)
, в)  , г)
, г)  .
. , б)
, б)  , в)
, в) 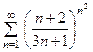 , г)
, г) 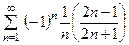 .
. , б)
, б)  , в)
, в)  , г)
, г)  .
. , б)
, б)  , в)
, в)  , г)
, г)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б)  , в)
, в)  .
. , б)
, б) 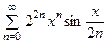 , в)
, в)  .
.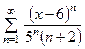 , б)
, б)  , б)
, б)  .
. .
.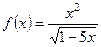 ;
;  , б)
, б)  ;
;  ;
; 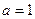 .
.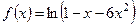 ;
;  ;
;  ;
;  .
. ;
; 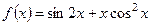 ;
;  ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
; 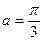 .
. ;
; 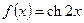 ;
;  ;
;  .
. ;
; 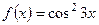 ;
;  ;
; 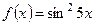 ;
;  ;
;  ;
;  .
. ;
;  ;
;  ;
;  ;
; 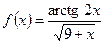 ;
;  ;
; 
 2.
2. 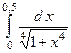 3.
3.  4.
4.  5.
5. 
 7.
7. 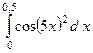 8.
8.  9.
9.  10.
10.  .
.
 2.
2. 

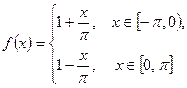
 ,
,  ,
, 


 ,
,  10.
10.  ,
,  2.
2.  3.
3.  4.
4. 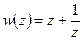
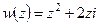 6.
6. 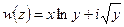 7.
7.  8.
8. 
 10.
10. 
 . 2.
. 2.  3.
3.  . 4.
. 4.  .
. . 6.
. 6.  . 7.
. 7.  8.
8.  .
. . 10.
. 10. 
 , если
, если 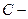 окружность радиуса 3 с центром в начале координат.
окружность радиуса 3 с центром в начале координат. , если
, если  внутри.
внутри. , если
, если 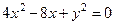 .
. , если
, если  .
. , если
, если  .
. по контуру
по контуру 
 .
. , если известно, что точки
, если известно, что точки  и
и  лежат внутри области, ограниченной контуром
лежат внутри области, ограниченной контуром  .
. , если
, если 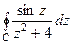 , где
, где 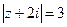 .
.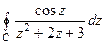 , где
, где  б)
б) 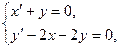

 ,
,  б)
б) 
 .
.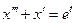 ,
,  б)
б) 
 .
. ,
,  б)
б) 
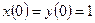
 ,
, 
 ,
, 

 ,
, 
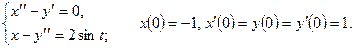
 ,
, 

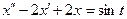 ,
,  б)
б) 
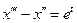 ,
,  .
.