НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ Р.Е. АЛЕКСЕЕВА»
Отчёт о практическом занятии №1 по методам оптимизации информационных систем
на тему: “Прямые методы оптимизации функции одной переменной”
Работу выполнила: студент(ка) гр. АЗИС 2013-3 Фамилия И.О. Работу проверил: ст. преп., к.ф.-м.н. Мазуров А.Ю.
Арзамас 2014 г.
Прямые методы оптимизации – методы, не требующие вычисления производной функции. Для их применения достаточно вычислить значения функции
1. Метод перебора – простейший метод. Применяется к унимодальным функциям. Задача: на отрезке Решение задачи: отрезок разбивают на n равных частей точками деления:
Вычислим значение функции в точках
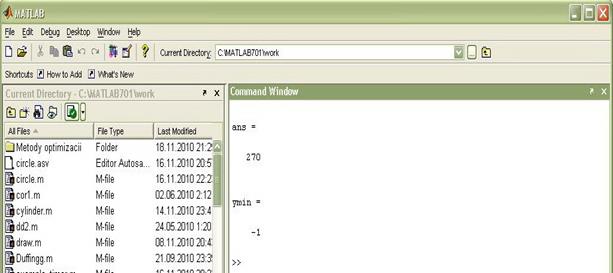
Тогда погрешность определения точки минимума составляет Текст программы: clear all clc a=pi/2; %отрезок b=3*pi/2; tochn=1/100; % точность shag=(b-a)*tochn; %шаг разбиения x=a:shag:b; [ymin xmin]=min(sin(x)); x(xmin)*180/pi %градусы в радианы ymin X = pi/2:0.001:3*pi/2; Y = sin(X); plot (X,Y); hold on
Полученный результат:
Полученный результат:
2. Метод поразрядного поиска Отличия от предыдущего метода: а) если оказывается, что б) сначала определяем отрезок, содержащий оптимальную точку, грубо, т.е. находим точку В этом методе перебор точек отрезка происходит сначала с шагом
Задача: минимизировать функцию Текст программы: clear all clc a=-1; b=2; shag=0.1; %шаг tochn=0.0001; %точность x=a; f_x=x^2-2*x+2; x=x+shag; f_x1=x^2-2*x+2; i=1; while shag>tochn while f_x1<=f_x f_x=f_x1; x=x+shag*i; f_x1=x^2-2*x+2; end f_x=f_x1;
shag=shag/4; i=-i; if x>b break; end end x fmin=f_x X = -1:0.001:2; Y = X.^2-2.*X+2; plot (X,Y); hold on Полученный результат:
3. Первый метод дихотомии («деления пополам») Задача: минимизировать функцию Для решения задачи необходимо разбить заданный отрезок пополам и взять две симметричные относительно центра точки § если § если Процедура повторяется, пока не будет достигнута заданная точность, НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Р.Е. АЛЕКСЕЕВА»
Отчёт о практическом занятии №2 по методам оптимизации информационных систем
на тему: “Методы оптимизации функции одной переменной, использующие производные”
Работу выполнила: студент(ка) гр. АЗИС 2013-3 Фамилия И.О. Работу проверил: ст. преп., к.ф.-м.н. Мазуров А.Ю.
Арзамас 2014 г.
1. Метод средней точки Данный метод оптимизации использует производную. Средняя точка Проверяем знак произведения: если Задача: минимизировать функцию clear all clc a=-3; b=0.75; x=(a+b)/2; f1=(1-x^2)/(x^2+1)^2; tochn=0.0001; while abs(f1)>=eps f1=(1-x^2)/(x^2+1)^2; fa=(1-a^2)/(a^2+1)^2; if f1*fa<0 b=x; else a=x; end x=(a+b)/2; end; x y=x/(x^2+1) X = -3:0.001:0.75; Y = X./(X.^2+1); plot (X,Y); hold on
2. Метод хорд Метод секущих (хорд) является более экономичным по сравнению с методом Ньютона по количеству функций, подлежащих расчету: на каждой итерации в методе секущих необходимо рассчитать только значение
получим значения коэффициентов Тогда
Если
Вычисления продолжаются, пока
|

 .
. . задана функция y=sin x. Необходимо минимизировать функцию на данном отрезке.
. задана функция y=sin x. Необходимо минимизировать функцию на данном отрезке. ,
, 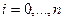
 , найдём путём сравнения точку, в которой
, найдём путём сравнения точку, в которой .
.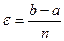 .
.

 , то отпадает необходимость вычислять значение функции в точках
, то отпадает необходимость вычислять значение функции в точках 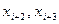 и т.д.
и т.д.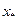 с небольшой точностью, а затем ищем её на этом отрезке с меньшим шагом дискретизации, повышая точность.
с небольшой точностью, а затем ищем её на этом отрезке с меньшим шагом дискретизации, повышая точность. до тех пор, пока не выполнится условие
до тех пор, пока не выполнится условие  или пока очередная из точек не совпадет с концом отрезка. После этого шаг уменьшается:
или пока очередная из точек не совпадет с концом отрезка. После этого шаг уменьшается:  , и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения
, и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения  снова не перестанут уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит
снова не перестанут уменьшаться или очередная точка не совпадет с другим концом отрезка и т.д. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит  .
. на отрезке
на отрезке  .
.

 на отрезке
на отрезке  с точностью 0.001.
с точностью 0.001.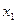 и
и 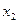 так, что
так, что  ,
,  , где
, где  — некоторое число в интервале от 0 до
— некоторое число в интервале от 0 до  . Затем отбросим тот из концов изначального интервала, к которому ближе оказалась одна из двух вновь поставленных точек с максимальным значением, т. е.:
. Затем отбросим тот из концов изначального интервала, к которому ближе оказалась одна из двух вновь поставленных точек с максимальным значением, т. е.: , то берём отрезок
, то берём отрезок  , отбрасывая
, отбрасывая  ,
, , то берём отрезок
, то берём отрезок  , отбрасывая
, отбрасывая 
 .
. 
 ,
,  .
. , то точка минимума находится на отрезке
, то точка минимума находится на отрезке  , а если не выполняется – то на отрезке
, а если не выполняется – то на отрезке  . И так далее, вычисления продолжаются, пока
. И так далее, вычисления продолжаются, пока  .
. на отрезке
на отрезке  .
.

 , т.к. значение
, т.к. значение  уже известно из предыдущей итерации.
уже известно из предыдущей итерации.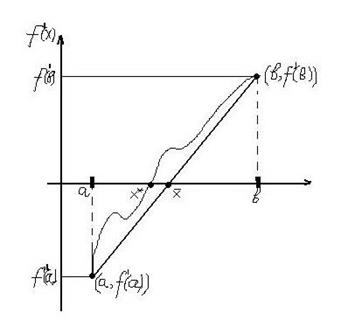
 - уравнение хорды.
- уравнение хорды.
 ,
,  .
. ,
,
 ,
,
 , то выбирается отрезок
, то выбирается отрезок  , то выбирается отрезок
, то выбирается отрезок 


