СОВЕРШЕННО СЕКРЕТНО! ТОЛ ЬКО
Оглавление. § 1. Общая постановка задачи.................................................................................................................... 3 § 2. Метод сведения краевой задачи к задаче Коши................................................................................ 3 § 3. Метод конечных разностей................................................................................................................. 4 § 4. Метод Галеркина.................................................................................................................................. 5 § 5. Метод прогонки.................................................................................................................................... 6 § 6. Программы............................................................................................................................................ 7 § 7. Результаты........................................................................................................................................... 12
В курсовой работе по численным методам требуется решить краевую задачу для обыкновенного дифференциального уравнения вида: 1. Методом сведения краевой задачи к задаче Коши. 2. Методом конечных разностей. 3. Методом Галёркина. Задание (вариант № 28).
§ 2. Метод сведения краевой задачи к задаче Коши. Пусть дано линейное дифференциальное уравнение:
где функции: p(x), q(x), f(x) непрерывны. Требуется найти решение уравнения (1), удовлетворяющее краевым условиям:
где: Решение будем искать в виде: y = cu + v (3), где: u = u(x) – ненулевое решение соответствующего неоднородного уравнения:
а v = v(x) – какое-нибудь решение данного неоднородного уравнения (1):
Очевидно, что функция, определенная формулой (3) является искомым решением уравнения (1), где с – произвольная постоянная. Потребуем, чтобы первое краевое условие (2) выполнялось для y при любом с. Используя его, будем иметь:
Для того чтобы последнее равенство было справедливо при любом с, необходимо и достаточно, чтобы коэффициент при с обращался в 0, т.е., было выполнено следующее:
Для обеспечения равенств (7-8) достаточно, например, положить:
где: k – постоянная, отличная от 0;
если
если Отсюда видно, что u есть решение задачи Коши для однородного уравнения (4), удовлетворяющее начальным условиям (9), а v есть решение задачи Коши для неоднородного уравнения (5), удовлетворяющее начальным условиям (10) или (11). При этом для любого с функция y = cu + v удовлетворяет краевому условию на конце x = a. Подберем постоянную c так, чтобы функция y удовлетворяла краевому условию (2) на другом конце отрезка y = b. Это дает:
Таким образом, краевая задача (1-2) сведена к двум задачам Коши для функций u(x) и v(x). Замечание 1. Если выполнено условие (12), то краевая задача (1-2) имеет единственное решение. Если же условие не выполняется по каким-либо причинам, то исходная задача может либо –вообще не иметь решений, либо их бесчисленное множество. Замечание 2. Если исходное уравнение (1) является однородным, т.е.: f(x) º 0, и кроме того, A = 0, то в силу условий (10) или(11) имеем:
§ 3. Метод конечных разностей. Рассмотрим линейное дифференциальное уравнение:
с линейными двухточечными краевыми условиями:
При этом снова полагаем:
Значения искомой функции y(x) в точках деления xi и ее производных Заменяя производные правыми односторонними конечно-разностными отношениями, для внутренних точек отрезка xi будем приближенно иметь:
Для концевых точек x 0 = a, xn = b полагаем:
Используя формулы (3), дифференциальное уравнение (1) можно при x = xi (i = 1, 2, …, n -1) приближенно заменить линейной системой уравнений:
Кроме того, в силу формул (4) краевые условия (2) дополнительно дают еще 2 уравнения:
Таким образом, мы получили линейную систему n + 1 уравнений с n + 1 неизвестными y 0, y 1, …, yn, которые представляют собой не что иное, как значения искомой функции y = y(x) в точках x 0, x 1, …, xn. Решив такую систему, получим таблицу значений искомой функции y. Замечание. Более точные формулы получаются, если воспользоваться симметричными конечно-разностными отношениями:
Для производных в концевых точках в общем случае приходится использовать формулы (4). Отсюда приходим к системе:
Для решения систем подобного рода разработан и применяется так называемый метод прогонки, о котором речь пойдет в § 5.
§ 4. Метод Галеркина. Данный метод основан на одной теореме из теории общих рядов Фурье. Теорема. Пусть: { un(x) } – полная система функций с ненулевой нормой, ортогональных на отрезке [ a; b ]. Если непрерывная функция f(x) ортогональна на отрезке [ a; b ] ко всем функциям un(x), т.е.:
то: f(x) º 0 при a £ x £ b. Замечание. Под нормой подразумевается: Переходим к рассмотрению метода Галеркина. Пусть имеется линейная краевая задача: L[y] = f(x) (2), где:
(при этом снова предполагается, что: Выберем конечную систему базисных функций { ui(x) }(i = 0, 1, …, n), составляющих часть некоторой полной системы, причем позаботимся, чтобы функция u 0(x) удовлетворяла неоднородным краевым условиям:
При нашем подборе базисных функций ui(x) функция y, очевидно, удовлетворяет краевым условиям (3) при любом выборе коэффициентов Ci. Если (4) подставить в (2), то получим невязку: Согласно методу Галеркина, требуем, чтобы невязка R была ортогональна базисным функциям, что при достаточно большом числе этих функций обеспечивает малость невязки в среднем. Для определения коэффициентов Ci приходим к системе линейных уравнений: или, более подробно:
§ 5. Метод прогонки. Рассмотрим линейное дифференциальное уравнение (1)[1] с двухточечными линейными краевыми условиями (2). От дифференциального уравнения (1) обычным приемом переходят к конечно- разностным уравнениям. Для этого разобьем отрезок [ a; b ] на n равных частей с шагом pi = p(xi), qi = q(xi), fi = f(xi), yi = y(xi),получаем при x = xi вместо дифференциального уравнения (1) следующее конечно-разностное уравнение
Введя обозначения:
причем из краевых условий (2) имеем
Линейная система (4),(5) состоит из n + 1 уравнений относительно n + 1 неизвестных Разрешая уравнение (4) относительно y i +1,находим:
Предположим, что с помощью полной системы (4) из уравнения исключен член, содержащий yi. Тогда уравнение (6) может быть записано в виде:
где коэффициенты
Но согласно формуле (7) имеем:
Отсюда, сравнивая формулы (8) и (9), находим:
Пусть теперь i>0 (i=1,2,.....n-2). Выражая yi поформуле (7), получим:
Отсюда, сравнивая формулы (7) и (11), получаем для коэффициентов Сi и Di рекуррентные формулы:
На основании формул (12), используя формулы (10) для С 0 и D 0, можно последовательно определить коэффициенты Сi и Di (i =1, 2,..., n - 2) до Сn -2 и Dn -2 включительно (прямой ход). Из формулы (7) при i = n - 2 и второго краевого условия (5) получаем:
Теперь используя формулу (7) и первое краевое условие (5), мы можем последовательно найти yn -1, yn -2, ..., y 0 (обратный ход).
§6. Программы. 1. Метод сведения к задаче Коши. #include <stdio.h> #include <conio.h> #include <math.h> #define p(x) (-3*(x)) #define q(x) (-4) #define r(x) (1) #define N 500 #define EPS 0.0001 void runge_kutt (void); int n; double y[N]; double a=1, b=1.6, A=-3.3, B=-2; double h=0.06, x; main () { int i, t; double y1[N], eps[N], max_eps; for (i=0;i<N;i++) y1[i]=0; clrscr (); do { for(i=0;i<=n;i++) y1[i]=y[i]; n=(b-a)/h+.5; if (n>N) { printf ("\n Ошибка: выход за пределы массива "); getch (); return 0; } runge_kutt (); max_eps=0; for (i=0;i<=n/2;i++) { eps[i]=fabs(y[2*i]-y1[i]); if (eps[i]>max_eps) max_eps=eps[i]; } h/=2; } while (max_eps>EPS); clrscr (); printf (" Решение краевой задачи дли дифференциального уравнения \n\ II- порядка с точностью Е = %методом сведения к задаче Коши \n\n",EPS);
printf ("ЙНННННННННННННЛННННННННННННННННННННННЛННННННННННННННННННН»\n"); for (i=0;i<=n/2;i+=(0.06/(h*4)+0.06)) printf ("є x = %.2f є y(x) = %+f є eps = %.1e є\n",a+h*4*i,y1[i],eps[i]); printf ("ИНННННННННННННКННННННННННННННННННННННКНННННННННННННННННННј\n");
printf ("\n Результаты представлены с шагом 0.06\n"); printf ("\заданная точность достигнута при шаге, равном %g\n",EPS,h*4); getch (); return 0; }
/****************************************************************************** Функция, вычисляющая корни дифференциального уравнения II порядка методом Рунге – Кутта после сведения его к задаче Коши. ******************************************************************************/
void runge_kutt (void) { int i; double u[N], v[N], z[N], g[N], x, c; double ku1,ku2,ku3,ku4,kz1,kz2,kz3,kz4; double tv1,tv2,tv3,tv4,tg1,tg2,tg3,tg4; z[0]=1; u[0]=0; v[0]=A; g[0]=0; for (i=0;i<=n;i++) { x=a+h*i; ku1=z[i]; kz1=-p(x)*z[i]-q(x)*u[i]; tv1=g[i]; tg1=-p(x)*g[i]-q(x)*v[i]+r(x); ku2=z[i]+h/2*kz1; kz2=-p(x+h/2)*(z[i]+h/2*kz1)-q(x+h/2)*(u[i]+h/2*ku1); tv2=g[i]+h/2*tg1; tg2=-p(x+h/2)*(g[i]+h/2*tg1)-q(x+h/2)*(v[i]+h/2*tv1)+r(x+h/2); ku3=z[i]+h/2*kz2; kz3=-p(x+h/2)*(z[i]+h/2*kz2)-q(x+h/2)*(u[i]+h/2*ku2); tv3=g[i]+h/2*tg2; tg3=-p(x+h/2)*(g[i]+h/2*tg2)-q(x+h/2)*(v[i]+h/2*tv2)+r(x+h/2); ku4=z[i]+h*kz3; kz4=-p(x+h)*(z[i]+h*kz3)-q(x+h)*(u[i]+h*ku3); tv4=g[i]+h*tg3; tg4=-p(x+h)*(g[i]+h*tg3)-q(x+h)*(v[i]+h*tv3)+r(x+h); u[i+1] = u[i] + (ku1+2*(ku2+ku3)+ku4)*h/6; z[i+1] = z[i] + (kz1+2*(kz2+kz3)+kz4)*h/6; v[i+1] = v[i] + (tv1+2*(tv2+tv3)+tv4)*h/6; g[i+1] = g[i] + (tg1+2*(tg2+tg3)+tg4)*h/6; } c = (B-v[n])/u[n]; for (i=0;i<=n;i++) y[i] = u[i]*c + v[i]; }
2. Метод конечных разностей. #include <stdio.h> #include <conio.h> #include <math.h>
#define p(x) (-3*(x)) #define q(x) (-4) #define r(x) (1)
#define l(x) ((q(x)*h*h-2)/ (1+p(x)*h/2)) #define m(x) ((1-p(x)*h/2)/ (1+p(x)*h/2)) #define f(x) (r(x)*h*h / (1+p(x)*h/2))
#define N 500 #define EPS 0.0001
int n; double y[N]; double a=1, b=1.6, A=-3, B=-2; double h=0.06, x; void raznost (void); main () { int i, t; double y1[N], eps[N], max_eps; for (i=0;i<N;i++) y1[i]=0; clrscr (); do { for(i=0;i<=n;i++) y1[i]=y[i]; n=(b-a)/h+.5; if (n>N) { printf ("\n Ошибка: выход за пределы массива "); getch (); return 0; } raznost(); max_eps=0; for (i=0;i<=n/2;i++) { eps[i]=fabs(y[2*i]-y1[i]); if (eps[i]>max_eps) max_eps=eps[i]; } h/=2; } while (max_eps>EPS); clrscr (); printf (" Решение краевой задачи для дифференциального уравнения II порядка с точностью Е = %g методом конечных разностей \n\n",EPS);
printf ("ЙНННННННННННННЛННННННННННННННННННННННЛННННННННННННННННННН»\n");
for (i=0;i<=n/2;i+=(0.06/(h*4)+0.06)) printf ("є x = %.2f є y(x) = %+f є eps = %.1e є\n",a+h*4*i,y1[i],eps[i]);
printf ("ИНННННННННННННКННННННННННННННННННННННКНННННННННННННННННННј\n");
printf ("\n Результаты представлены с шагом 0.06"); printf ("\n ‡ ¤ п в®з®бвм %g ¤®бвЁЈгв ЇаЁ и ЈҐ а ў® %g\n",EPS,h*4); getch (); return 0; }
/**************************************************************************** Функция, вычисляющая корни уравнения II порядка методом конечных разностей. ****************************************************************************/
void raznost (void) { int i; double c[N], d[N]; y[0]=A; y[n]=B; c[0]=A; d[0]=0; for (i=1;i<=n;i++) { x = a + h*i; c[i]=(f(x)-m(x)*c[i-1])/(l(x)-m(x)*d[i-1]); d[i]=1/(l(x)-m(x)*d[i-1]); } for (i=n-1;i>=1;i--) y[i]=c[i]-d[i]*y[i+1]; }
3. Метод Галеркина. #include<stdio.h> #include<math.h> #include<conio.h>
#define P(x) (-3*(x)) #define Q(x) (-4) #define R(x) (1)
#define M 11 main() { double a=1,b=1.6,A=-3.3,B=-2,eps=0.0001; double x,y[M][2],u,l,c[M],h,s1,s2,w,norm,n1[M],I[M][M],J[M]; int N=10,Q=10,i,p=0,j,v,s,n=2; clrscr(); do { h=(b-a)/N;n1[0]=0;n1[10]=0;s1=0;s2=0;y[0][p]=A;norm=0; for(v=1;v<=n;v++) for(i=1;i<=n;i++) { for(j=1;j<N;j++) { x=j*h+a; u=pow(x-a,i)*(x-b); l=v*pow(x-a,v-2)*((v-1)*(x-b)+2*(x-a))+ P(x)*(v*pow(x-a,v-1)*(x-b)+pow(x-a,v))+ Q(x)* pow(x-a,v) *(x-b); if(float(j)/2!=j/2) s1+=u*l; else s2+=u*l; } I[i][v]=h/3*(4*s1+2*s2); s1=0;s2=0; } for(i=1;i<=n;i++) { for(j=1;j<N;j++) { x=j*h+a; u=pow(x-a,i)*(x-b); l=P(x)*(B-A)/(b-a)+Q(x)*((A*b-B*a)/(b-a)+(B-A)/(b-a)*x); if(float(j)/2!=j/2) s1+=u*(R(x)-l); else s2+=u*(R(x)-l); } J[i]=h/3*(4*s1+2*s2); s1=0;s2=0; } for (s=1;s<n;s++) for (i=s+1;i<=n;i++) { w=I[i][s]/I[s][s]; J[i]-=J[s]*w; for(j=s+1;j<=n;j++) I[i][j]-=I[s][j]*w; } c[n]=J[n]/I[n][n]; for(i=n-1;i>0;i--) { c[i]=J[i]; for(j=i+1;j<=n;j++) c[i]-=I[i][j]*c[j]; c[i]/=I[i][i]; } for(j=1;j<=Q;j++) { x=j*(b-a)/Q+a; y[j][p]=(A*b-B*a)/(b-a)+(B-A)/(b-a)*x; for(i=1;i<=n;i++) y[j][p]=y[j][p]+c[i]*pow(x-a,i)*(x-b); } if(p==0) {p=1;n++;norm=eps+1;continue;} else { for(i=1;i<Q;i++) { n1[i]=fabs(y[i][0]-y[i][1]); if(n1[i]>norm) norm=n1[i]; } for(i=0;i<=Q;i++) y[i][0]=y[i][1]; } n++; } while (norm>eps); printf ("\n Решение краевой задачи для дифференциального уравнения \n" " II-го порядка с точностью Е = %g методом конечных разностей \n",eps); printf ("\nˆҐп %d га ўҐЁп\n",n-1); printf ("ЙНННННННННННННЛННННННННННННННННННННННЛННННННННННННННННННН»\n");
for(i=0;i<=Q;i++) printf ("є x = %.2f є y(x) = %+f є eps = %.1e є\n",i*(b-a)/Q+a,y[i][0],n1[i]); printf ("ИНННННННННННННКННННННННННННННННННННННКНННННННННННННННННННј\n"); printf ("\n Результаты представлены с шагом 0.06\n"); getch(); return 0; }
§ 7. Результаты. 1. Метод сведения к задаче Коши:
2. Метод конечных разностей[2]:
3. Метод Галеркина.
[1] Ссылки (1-2) на соответствующие формулы § 3. [2] Заданная точность достигнута при шаге h = 0.0075. СОВЕРШЕННО СЕКРЕТНО! ТОЛ ЬКО для командования!» ■;
|

 Решение необходимо произвести независимо тремя методами:
Решение необходимо произвести независимо тремя методами:
 (1),
(1), (2),
(2), - заданные константы, причем:
- заданные константы, причем:  и
и 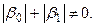
 (4),
(4), (5).
(5). или:
или: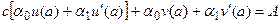 (6).
(6).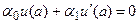 (7),
(7),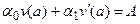 (8).
(8).
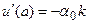 (9),
(9),
 (10),
(10),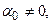 и:
и:
 (11),
(11),
 откуда:
откуда:  При этом предполагается, что знаменатель этого выражения отличен от нуля:
При этом предполагается, что знаменатель этого выражения отличен от нуля: (12).
(12). т.е., v º 0. Поэтому: y = cu(x), где u(x) – решение уравнения (4), удовлетворяющее начальным условиям (9). Очевидно, в этом случае:
т.е., v º 0. Поэтому: y = cu(x), где u(x) – решение уравнения (4), удовлетворяющее начальным условиям (9). Очевидно, в этом случае: 
 (1)
(1)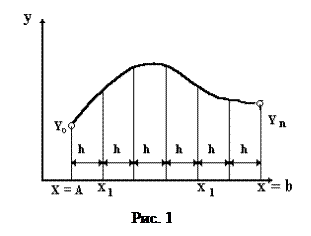 Одним из наиболее простых методов решения этой задачи является сведение ее к системе конечно-разностных уравнений. Разобьем отрезок [a; b] на n равных частей длины h (шаг), причем:
Одним из наиболее простых методов решения этой задачи является сведение ее к системе конечно-разностных уравнений. Разобьем отрезок [a; b] на n равных частей длины h (шаг), причем:  Точки разбиения имеют абсциссы: xi = x 0 + ih (i = 0, 1, 2, …, n); x 0 = a, xn = b (см. рис. 1).
Точки разбиения имеют абсциссы: xi = x 0 + ih (i = 0, 1, 2, …, n); x 0 = a, xn = b (см. рис. 1). обозначим через:
обозначим через: 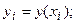

 Введем, кроме того, еще несколько новых обозначений:
Введем, кроме того, еще несколько новых обозначений: 


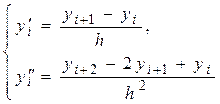 (3).
(3).
 (4).
(4). (i = 1, 2, …, n -1) (5).
(i = 1, 2, …, n -1) (5).
 (6).
(6). (i = 1, 2, …, n – 1) (7).
(i = 1, 2, …, n – 1) (7). (8).
(8). (n = 1, 2, …) (1),
(n = 1, 2, …) (1),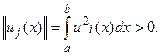
 и есть краевые линейные условия:
и есть краевые линейные условия: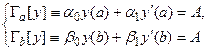 (3)
(3) ).
).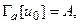
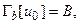 а функции ui(x) (i = 1, 2, …, n) удовлетворяли бы однородным краевым условиям:
а функции ui(x) (i = 1, 2, …, n) удовлетворяли бы однородным краевым условиям:  (i = 1, 2, …, n). Решение краевой задачи (2-3) будем снова искать в виде:
(i = 1, 2, …, n). Решение краевой задачи (2-3) будем снова искать в виде: (4).
(4). Для точного решения исходной задачи: R º 0, поэтому для получения приближенного решения, близкого к точному, нам выгодно подобрать коэффициенты Ci так, чтобы R ® 0.
Для точного решения исходной задачи: R º 0, поэтому для получения приближенного решения, близкого к точному, нам выгодно подобрать коэффициенты Ci так, чтобы R ® 0.
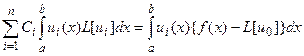 (i = 1, 2, …, n).
(i = 1, 2, …, n). Полагая;
Полагая; 

 и вводя обозначения:
и вводя обозначения: Отсюда после упрощения будем иметь:
Отсюда после упрощения будем иметь: (3),
(3),
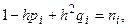 будем иметь:
будем иметь: (i = 0, 1, 2, …, n – 2) (4),
(i = 0, 1, 2, …, n – 2) (4),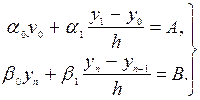 (5).
(5). Эту систему можно решить обычным способом. Однако существует более короткий.
Эту систему можно решить обычным способом. Однако существует более короткий. (6).
(6). (7),
(7), подлежат определению. Найдем формулы для этих коэффициентов. При i =0 из формулы (6) и краевых условий (5) следует, что:
подлежат определению. Найдем формулы для этих коэффициентов. При i =0 из формулы (6) и краевых условий (5) следует, что:
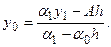 Исключая отсюда y, будем иметь:
Исключая отсюда y, будем иметь:  Разрешая это уравнение относительно y 1, будем иметь:
Разрешая это уравнение относительно y 1, будем иметь: 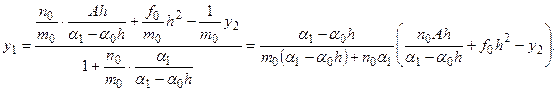 (8).
(8).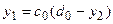 (9).
(9). (10).
(10). Подставляя это в (6), имеем:
Подставляя это в (6), имеем:  Разрешая это относительно yi + 1 будем иметь:
Разрешая это относительно yi + 1 будем иметь:  или:
или: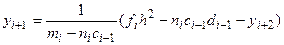 (11).
(11). (12).
(12).



