Построим доверительные интервалы для параметров модели.С вероятностью 0,95 построим доверительный интервал ожидаемой величины ущерба в предположении, что x0 = 40 ед. Построенная адекватная модель может использоваться для прогнозирования. Если известно значение независимой переменной х0, то прогноз зависимой переменной осуществляется подстановкой этого значения в полученное эмпирическое уравнение регрессии y0 = Доверительный интервал индивидуальных значений зависимой переменной y:
определяет границы, за пределами которых могут оказаться не более 95% точек наблюдений при Х = х0. Тогда, подставляя имеющиеся данные, получим:
Искомый доверительный интервал: (17,158; 26,53).
Вариант 6. Данные наблюдений представлены в таблице:
Диаграмма рассеяния.
2) Построим уравнение линейной регрессии: yi=α+βxi+εi Составим вспомогательную таблицу:
Найдем оценки неизвестных параметров с помощью метода наименьших квадратов, получим:
Уравнение регрессии будет: y = 58,482 + 2,434x
Построим доверительные интервалы для параметров модели. Формулы для расчета доверительных интервалов имеют следующий вид:
которые с надёжностью 95% накрывают определяемые параметры α и β. Для их нахождения построим вспомогательную расчетную таблицу:
Найдем стандартные ошибки коэффициентов регрессии:
где Тогда: S = 4,24
По таблице значений критерия Стьюдента находим
4) Проверим гипотезу, что а = 2,11: Выдвинем гипотезу, о том, что коэффициент регрессии а равен 2,11, т.е. H0: а = 2,11. Поскольку в вычислениях пункта 3)
а не попадает в доверительный интервал, гипотеза H0: а = 2,11 отвергается.
5) Оценим статистическую значимость коэффициентов регрессии а и b:
|
.
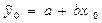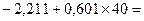21,844
,
,
- стандартная ошибка коэффициента регрессии a.
- стандартная ошибка коэффициента регрессии b,
, 
= 3,253
0,456
, тогда, подставляя в формулы интервалов известные данные, получим доверительные интервалы:
