Парная регрессия и корреляция. Описывая различные методы технического анализа в этой книге, мы буквально в каждом случае касались проблемы их оптимизации12
Описывая различные методы технического анализа в этой книге, мы буквально в каждом случае касались проблемы их оптимизации. Введение методов компьютерного анализа позволяет исследователям товарных рынков значительно усовершенствовать проверенные временем методики путем подбора оптимальных значений для их основных показателей. Это в полной мере относится к работе с пункто-цифровыми графиками. В связи с этим, однако, возникает одна проблема, заключающаяся в необходимости периодического повторного оптимизирования параметров графика. Насколько часто их следует подвергать очередной оптимизации? Раз в квартал, раз в полгода, ежегодно? Процессы испытаний каждой новой оптимизированной версии занимают много времени и требуют значительных затрат. Трейдер сам должен решить, стоит ли постоянная оптимизация пункто-цифрового метода того времени и денег, которые на нее уходят. (См. рис. 12.6 а-в.) ИСТОЧНИКИ Тем, кто желает получать уже готовые пункто-цифровые графики, можно посоветовать обратиться в любую из пяти существующих информационных служб. Традиционные графики, основанные на трехклеточной реверсировке, для товарных фьючерсных рынков публикует компания "Чарткрафт коммодити сервис". Сходные графики для рынков США и Великобритании можно получать через лондонское агентство "Чарт аналисиз лимитед" (см. рис. 12.7). Оптимизированные графики публикуют два агентства: "Коммодити прайс чартс" и "Данн энд Харгитт эдвайзори сервис" (см. рис. 12.6в). Сравнительная таблица параметров традиционного и оптимизированных графиков
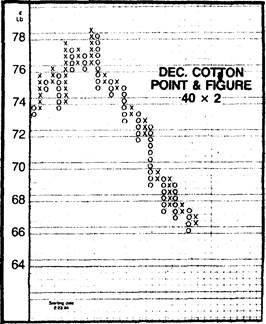
Рис. 12. 6а Примеры традиционного (справа) и оптимизированного (слева) графиков. Обратите внимание, что оптимизированный график намного чувствительнее обычного - на нем появляется больше сигналов.
Что же касается внутридневных пункто-цифровых графиков, то их распространяет только компания "Куотрон фьючерз чартс". Электронные внутридневные графики в течение последних десяти лет распространяла в основном информационная служба "Видеком комтренд". Ее клиенты получают не только сами графики на экран компьютера или в виде распечатки, но также цифровые данные в чистом виде, с помощью которых можно строить графики самостоятельно. В предыдущей главе мы уже говорили о новой информационной службе, появившейся недавно: "Маркет Вижн", которая не предоставляет данные для ручного построения графиков, однако поставляет пользователю наглядные и красиво оформленные пункто-цифровые графики (каждый второй день на электронном графике изображен разным цветом). Агентство "Ком-путрэк" также распространяет пункто-цифровые графики, но только модифицированного типа (см. рис. 11.2-4, гл. 11). Другие службы также расширяют ассортимент услуг, предоставляемых клиентам, которые предпочитают работать с пун-кто-цифровыми графиками.
Рис. 12.6в Примеры оптимизированных пункто-цифровых графиков. Что касается литературы, то наиболее исчерпывающим источником информации по внутридневным пункто-цифро-вым графикам служит книга А. Уилана "Руководство по пункто-цифровому методу" (Study Helps in Point and Figure Technique, A. Wheelan). Более сжатой версией данной работы является статья указанного автора под названием "Пункто - цифровой метод в анализе товарных фьючерсных рынков", опубликованная в сборнике "Руководство по прогнозированию фьючерсных цен". Тем, кто интересуется методом трехклеточной реверсировки, лично я посоветовал бы почитать книгу "Использование пункто-цифрового метода трехклеточной реверсировки на рынке ценных бумаг" (The Three-Point Reversal Method of Point and Figure Stock Market Trading). Для более глубокого изучения проблем оптимизации пункто-цифровых графиков лучше всего обратиться к уже упоминавшейся книге Зига и Кауфмана "Пункто-цифровые методы в операциях на товарных рынках".
Рис. 12.7 Примеры графиков для американских и британских рынков золота. ЗАКЛЮЧЕНИЕ Мы завершаем довольно подробное изучение пункто-цифрового метода технического анализа рынка. Мы рассмотрели классический внутридневной метод, модифицированный метод трехклеточной реверсировки, а также способы оптимизации пункто-цифровых графиков. Необходимо подчеркнуть, что столбиковые графики должны оставаться основным инструментом графического анализа операций на фьючерсных рынках. Тем не менее, было бы неразумно ограничиваться только ими, полностью отказавшись от пункто-цифрового графика. Для трейдеров, специализирующихся на сверхкраткосрочных сделках, внутрид-невные пункто-цифровые графики просто незаменимы. Даже позиционные трейдеры могут успешно использовать внут-ридневные графики для выбора наиболее удачных моментов входа в рынок и выхода из него. Графики такого типа хороши не только для краткосрочных сделок, но и вполне пригодны для долгосрочных операций. Для тех трейдеров, которым недостает времени и средств, необходимых для работы с внутридневными графиками, существует модифицированная версия, основанная на трехклеточной реверсировке, а также графики с оптимизированными параметрами. Благодаря своей практически неограниченной гибкости и высокой точности сигналов, пункто-цифровой метод служит отличным дополнением к столбиковым графикам. В заключение стоит упомянуть еще одно обстоятельство, связанное с применением пункто-цифрового метода. Данный метод можно с успехом использовать для построения стандартных технических индикаторов. Различные осцилляторы, например индекс относительной силы (RSI), а также балансовый объем (OBV) можно строить в виде пункто-цифрового графика. Прорывы и другие особенности динамики цен, фиксируемые индикаторами, на пункто-цифровом графике представлены более четко и ясно. В общем, смело овладевайте пункто-цифровым методом, а как его применять при решении конкретных задач на рынке, вам подскажет воображение.
Парная регрессия и корреляция Парная регрессия представляет собой регрессию между двумя переменными –
где
где Случайная величина От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака К ошибкам спецификации относятся неправильный выбор той или иной математической функции для Наряду с ошибками спецификации могут иметь место ошибки выборки, которые имеют место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии. Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например, в результате наличия скрытых доходов. Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. В парной регрессии выбор вида математической функции 1) графическим; 2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи; 3) экспериментальным. При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 1.1:
Рис. 1.1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными. Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков. При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических
Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным. Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной 12
|





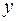 и
и 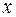 , т. е. модель вида:
, т. е. модель вида: ,
, ,
, – теоретическое значение результативного признака, найденное исходя из уравнения регрессии;
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии; 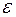 – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. может быть осуществлен тремя методами:
может быть осуществлен тремя методами:







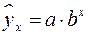
 , рассчитанной при разных моделях.
, рассчитанной при разных моделях.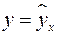 , т.е. они полностью обусловлены влиянием фактора
, т.е. они полностью обусловлены влиянием фактора  .
. . Величина этих отклонений и лежит в основе расчета остаточной дисперсии:
. Величина этих отклонений и лежит в основе расчета остаточной дисперсии: .
.


