Лист ответов
1. Дать определение действительного числа. Объяснить, как устанавливается взаимно-однозначное соответствие между действительными числами и точками числовой оси. 2. Дать определение различных видов промежутков на оси (отрезок, интервал, полуинтервал и т.п.). Дать определения окрестностей точки на оси (e-окрестности, проколотой e-окрестности, полуокрестностей). Дать определение окрестностей +¥ и –¥. 3. Дать определения множества, ограниченного сверху (снизу), ограниченного множества. Доказать эквивалентность двух определений ограниченного множества. 4. Дать определения верхней и нижней граней множества. Привести примеры ограниченных сверху (снизу) множеств, содержащих и не содержащих свою верхнюю (нижнюю) грань. 5. Сформулировать теорему о существовании верхней (нижней) грани у множества. 6. Объяснить понятие отображения. Дать определение функции. Дать определение числовой последовательности, привести примеры. 7. Дать определения (в различных формах) пределов 8. Доказать ограниченность последовательности, имеющей конечный предел. Показать на примерах, что обратное утверждение неверно. 9. Доказать теорему о единственности предела последовательности. 10. Сформулировать теоремы о пределах суммы, произведения и частного двух последовательностей. 11. Дать определение подпоследовательности. Доказать, что подпоследовательность последовательности, имеющей предел, имеет тот же предел. 12. Дать определения бесконечно большой и бесконечно малой последовательностей. Привести примеры. 13. Доказать теорему Вейерштрасса о существовании предела у неубывающей ограниченной сверху последовательности. Сформулировать варианты этой теоремы. 15. Сформулировать следующие определения пределов (при помощи неравенств и при помощи окрестностей).
16. Дать определение бесконечно малой функции при 17. Доказать теорему о локальной ограниченности функции, имеющей конечный предел. 18. Доказать теорему о пределе суммы двух функций при 19. Доказать теорему о пределе произведения двух функций при 20. Дать определение непрерывности функции в точке 1) при помощи понятия предела, 2) при помощи неравенств, 3) при помощи окрестностей, 4) при помощи приращений D х и D у.
Лист ответов
|

 ,
,  ,
,  .
.






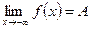





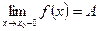
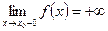

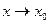 . Доказать теорему: функция f (х) имеет предел b тогда и только тогда, когда величина f (х) – b – бесконечно малая.
. Доказать теорему: функция f (х) имеет предел b тогда и только тогда, когда величина f (х) – b – бесконечно малая.


