Лабораторная работа №1. Изучение и измерение магнитного поля соленоида
Изучение и измерение магнитного поля соленоида
Цель работы: Ознакомится с различными способами получения и измерения магнитного поля. Ознакомится с простейшими инженерными расчетами источников магнитных полей. Провести измерение поля соленоида и определить его параметры.
Теория
1. Способы получения магнитных полей Существует два способа получения магнитного поля. В первом способе магнитное поле создается намагниченным веществом, именно так изготовляют постоянные магниты. В другом способе магнитное поле создается током протекающем по проводнику нужной конфигурации. Простейшим источником магнитного поля является виток с током. Поле на оси витка с током дается выражением:
здесь μ0 – магнитная проницаемость вакуума, R – радиус витка, I – ток, х – расстояние от центра витка. Поле в центре витка можно получить из предыдущего выражения:
Одиночный виток с током можно применить только для создания слабых магнитных полей. Значение магнитного поля Земли является естественным эталоном, относительно которого можно обсуждать сильные и слабые магнитные поля. Хотя поле Земли несколько меняется в зависимости от географического положения и геологических условий, но можно считать его приблизительно равным 0.5·10-4 Т или 0.5 Гс. Магнитное поле сравнимое с полем Земли можно получить с помощью витка радиусом 0.1 м при токе порядка 8 А. Катушка всего из 10 витков позволяет снизить ток в 10 раз, что позволяет без всяких технических проблем получать такие поля. Поскольку магнитные силовые линии проникают сквозь многие материалы, то при создании полей меньших или сравнимых с полем Земли требуется магнитная экранировка всей магнитной системы. В качестве магнитных экранов используют ферромагнитные материалы с высокой магнитной проницаемостью. В таких материалах магнитные силовые линии замыкаются в ферромагнетике и не проникают внутрь экранируемого объема. Создание магнитных полей, превышающих поле Земли не более чем в 100 раз, не составляет технической проблемы. Такие магнитные поля можно получить с помощью цилиндрических катушек – соленоидов или плоских катушек специальной конфигурации, например катушек Гельмгольца. Однако достижение более сильных полей с помощью катушек наталкивается на серьезные технические проблемы. Как видно из выражения (1.1) индукция поля пропорциональна току. В свою очередь сопротивление катушки растет пропорционально длине провода или приблизительно пропорционально числу витков. Соответственно для получения сильных магнитных полей требуется увеличивать ток, протекающий по катушке имеющей значительное сопротивление. Мощность выделяющаяся на обмотке согласно Р = I 2 ·R растет пропорционально квадрату тока. Существует правило: "Увеличение поля в 10 раз влечет за собой рост потребляемой мощности в 100 раз". В итоге при создании поля больше 0.1 Т выделяемое в катушке тепло становиться столь значительным, что требуется принудительное охлаждение. Обычно эта проблема решается путем покачивания через соленоид охлаждающей воды. Но и на этом пути возникают технические трудности. Соленоиды, предназначенные для получения полей от единиц до десятков тесла, потребляют от десятков до тысяч мегаватт мощности. Самые сильные источники поля являются уникальными сооружениями и применяются только в нескольких лабораториях в мире. Поскольку потребляемая мощность сравнима с энергопотреблением небольшого города. Для намотки можно воспользоваться сверхпроводящим проводом, сопротивление, которого при низких температурах равно нулю. В замкнутой накоротко катушке из сверхпроводящего провода может циркулирующий ток, который будет "вечно" создавать сильное поле без всяких затрат энергии. Однако очень сильные магнитные поля разрушают сверхпроводимость. Поэтому сверхпроводники обычно используют для создания полей в диапазоне до 10 Т. Но их применение зачастую ограничено из-за необходимости использования жидкого гелия. Частным методом для получения сверхсильных магнитных полей является импульсная генерация магнитного поля в небольших по размерам катушках. Но создаваемые таким способом поля существуют очень ограниченное время - обычно меньше долей секунды. Хотя этого часто оказывается достаточным для проведения научных исследований. Для создания магнитных полей больше 0.1 Т часто используют комбинацию катушки и сердечника из ферромагнитных материалов. По этому принципу устроены электромагниты. По сравнению с соленоидом электромагнит потребляет в десятки раз меньше мощность. Но электромагниты становятся столь же неэкономичными и громоздкими сооружениями, когда требуется получить поле, превышающее поле насыщения железа. По этой причине электромагниты редко применяются для создания поля большего, чем 2 Т. Постоянные магниты также применяются для создания магнитных полей. Особенно в тех случаях, когда поле не требуется изменять в пределах больших нескольких процентов от номинала. Магниты на основе традиционных сплавов ферромагнитных материалов, таких как железо, кобальт никель, не позволяют создать поля большие, чем 0.8 Т. Только магниты, в составе которых применяются редкоземельные элементы, такие как самарий или неодим позволяют получить поля до 1 Т.
2. Индукция магнитного поля соленоида Как известно из общей физики поле созданное в бесконечном соленоиде можно определить из следующего выражения: В = m0 I · n, (1.2) где I ток в соленоиде, а п число витков на единицу длины соленоида. На практике некоторым приближением к бесконечному соленоиду будет длинная катушка, у которой диаметр в несколько раз меньше длины. Очевидно, что поле внутри соленоида конечной длины будет изменяться вдоль оси катушки, достигая максимума вблизи середины и плавно уменьшаясь к торцам. Легко понять, что у торца полубесконечного соленоида магнитное поле будет в два раза меньше, чем у бесконечного соленоида. Таким образом, у длинного соленоида поле у его торцов уменьшается примерно в два раза по сравнению с полем в центре соленоида. Поэтому область однородного поля находиться только в ограниченной области вблизи центра соленоида. Если от соленоида требуется получение однородного поля большого объема, то его стремятся максимально приблизить к бесконечному соленоиду. Чтобы получить достаточно большую однородную область, диаметр катушки и отношение длины к диаметру следует выбирать возможно большими (например, порядка 3: 1). Однако, вследствие вытянутой формы соленоида доступ к рабочей области неудобен; поэтому соленоиды применимы не для всяких видов магнитных измерений. Падение напряженности магнитного поля вдоль оси соленоида можно уменьшить, увеличивая число витков на концах катушки, или располагая там дополнительные обмотки. Для получения большей однородности вдоль оси можно даже ослабить поле в середине, используя для этого вторую обмотку.
Получим выражение для магнитного поля соленоида конечной длины (рис. 1). Пусть число витков на единицу длины n и участок dz содержит n · dz витков, которые, согласно выражению (1.1) для поля витка с током, в точке на оси соленоида создадут индукцию
здесь r = (R 2 + x 2)½. Из рис. 1 видно, что
Подставляя (1.4) в (1.3) и интегрируя полученное выражение от q1 до q2, имеем
В случае бесконечного соленоида q1 ® 0, q2 ® p, и мы получим (1.2) В z = m 0 I · n. Чтобы для расчетов магнитного поля в этой работе можно было воспользоваться геометрическими размерами соленоида, выразим значения косинусов входящие в выражение (1.5). Учтем, что cosq2 = cos(180 – q3) = – cosq3 (рис. 1), тогда
Начало координат поместим в центр соленоида и обозначим
получим:
Из выражения (1.6) можно рассчитать поле в любой точке на оси соленоида, как внутри, так и вне соленоида. Для этого необходимо знать длину соленоида L, радиус R, ток I, число витков на единицу длины n и задать расстояние z от центра соленоида. Необходимо только вычислить косинусы углов q1 и q2.Надо учитывать, что выражения (1.5, 1.6) строго применимы только для однослойного соленоида. Однако в случае, когда толщина обмотки соленоида меньше его радиуса они также применимы. В этом случае число витков на единицу длины определяется как n = N / L, где N – полное число витков. Кроме того, в выражения (1.8) должен войти средний радиус намотки.
Для поля в центре z = 0 и выражения (1.7) и (1.8) упрощаются: θ1 = θ3 = θ0 и cos θ1 = – cos θ3 Соответственно В = m0 I · n ·cosθ0. Как видно отличие от формулы для бесконечного соленоида выражается только в геометрическом множителе: К = cosθ0. Для расчета геометрических множителей удобно прейти к половинной длине соленоида. Обозначим L /2 = l. Здесь l полудлина соленоида. Тогда а = b = l и К = l /(R 2 + l 2)1/2. Окончательно получим:
В = m0 I · n · l /(R 2 + l 2)1/2, (1.9)
где l – половина длины соленоида, в качестве R – обычно принимается средний радиус намотки. Однако точные формулы учитывающие толщину намотки выглядят более сложными. В рамках этой работы они не рассматриваются. 3. Порядок расчета соленоида Предположим, что величина поля в соленоиде задана. Для оценочного расчета можно применить формулу (1.2) для бесконечного соленоида, откуда определяется произведение тока на число витков на единицу длины. Дальнейший расчет сводиться к разделению в этом произведении величины тока и количества витков. А также уточнения всех геометрических величин для реального соленоида. Обычно известен размер объектов, которые будут подвергаться воздействию поля. Геометрический размер объектов определяет минимальный диаметр соленоида и требуемый объем однородного поля. Исходя из протяженности области однородного поля, можно выбрать минимальную длину соленоида, руководствуясь теоретическим выражением распределения поля вдоль оси z (1.6). В первом приближении можно положить, что длина соленоида должна быть втрое больше радиуса. Можно показать, что в этом случае поле в центре реального соленоида будет на 3% меньше поля в бесконечном соленоиде, а протяженность области однородного поля будет порядка диаметра соленоида. Пусть из этих соображений получено, что R 1 – радиус внутреннего отверстия и первого слоя витков соленоида, а L – длина соленоида. При расчете соленоида, обмотка которого намотана медным проводом, следует учитывать её разогрев при протекании тока. При прохождении тока по проводам, имеющим свободный отвод тепла, например длинные провода в воздухе или в стенах зданий, допустимая плотность тока может достигать 7 - 10 А/мм2. Поскольку соседние витки разогревают друг друга, и тепло не успевает рассеяться, то для плотной многослойной намотки допускается меньшая плотность тока. В отсутствии принудительного охлаждения обычно выбирают плотность тока j = 2 – 3 А/мм2. При большой плотности тока соленоид просто перегреется и его обмотка сгорит. При дальнейшем расчете необходимо задаться неким параметром, который выбирают из практических соображений. Часто таковым является диаметр провода. Если выбирают диаметр провода d, то его сечение S = π d 2/4. В свою очередь I = j·S. Тогда подставив выражение для тока в (1.2) получим цепочку выражений: B = μ0 j·S·n. В свою очередь число витков на единицу длины n = N/L, где L – длина соленоида, N – общее число витков. Тогда требуемое для получения заданного поля число витков определиться из выражения: N = B·L /μ0 j·S. С другой стороны число витков, которые поместятся на длине соленоида при однослойной намотке N слоя = L / d. Если окажется, что N > N слоя, то число слоев определиться N / N слоя. Теперь можно оценить толщину намотки: h = N · d / N слоя. Поскольку ранее уже был определен минимальный радиус обмотки, то можно оценить габариты соленоида. Его наибольший радиус будет R 1+ h. Если окажется, что средний радиус обмотки R 1+ h /2 таков, что выбранное соотношение длины и радиуса соленоида не удовлетворяет требованию получения нужной однородности поля, то потребуется увеличить длину, с тем чтобы уменьшить число слоев намотки и средний радиус соленоида. Приведенных расчетов не достаточно, поскольку необходимо увязать их с параметрами источника питания. Из закона Ома I·R ом = U, где U напряжение источника тока, R ом – сопротивление соленоида. Если выбрать тонкий провод, то сопротивление обмотки R ом = ρ·l/S, где l – длина провода в катушке, а ρ – удельное сопротивлении меди (ρ = 0.017 Ом·мм2/м), окажется слишком большим и для питания соленоида потребуется высоковольтный источник. На практике это по многим соображениям неудобно. Поэтому стараются выбрать провод большего сечения, чтобы сделать общее сопротивление обмотки минимальным. С таким расчетом, чтобы уложиться в параметры уже имеющегося промышленного источника питания или не выйти за пределы напряжения нескольких сотен вольт. Для расчета сопротивления требуется определить реальную длину провода. Наиболее просто длина провода может быть оценена для соленоида, у которого намотано не больше нескольких слоев провода. Тогда можно считать, что в среднем длина провода в одном витке определиться: l витка = 2π·R сол, здесь R сол средний радиус обмотки. В каждом слое поместиться N слоя = L / d. Тогда полная длина провода определиться l провода = l витка N слоя. Таким образом, зная предполагаемые геометрические размеры соленоида, и задавшись сечением провода можно найти сопротивление обмотки и определить параметры источника питания. Для многослойной намотки воспользоваться приведенной выше методикой нельзя. Требуется точно рассчитать длину провода в вертикальном слое при спиральной намотке (рис. 2). Длина провода в пределах узкого кольца шириной d r составит d L вс = 2p· r ·d r / d, где d диаметр провода, а 1/ d – число витков на единицу толщины. L в с = R1∫R22p· r ·d r / d = p·(R 22 – R 12)/ d.
Длина спиральной намотки определяется по формуле: L в с = p·(R 22 – R 12)/ d (1.10) где R 2 и R 1 соответственно наружный и внутренний радиусы, а d – диаметр провода. Тогда полная длина провода составит l провода = L в с · N слоя. Сопротивление провода такой длины составит R ом= ρ · l провода/ S. Попутно можно определить и массу медного провода m = ηCu· l провода· S, здесь плотность меди ηCu = 8960 кг/м3. Зная ток и напряжение необходимо определить максимальную мощность Р = I·U. Если окажется, что потребляемая соленоидом мощность превышает 1 кВт, то потребуется провести тепловые расчеты, с тем чтобы выяснить потребуется ли принудительное охлаждение магнитной системы.
Имеет место уравнение теплового баланса: Р э = Р т и + Р т о, где Р э – электрическая мощность подводимая к соленоиду, Р т и – мощность теплового излучения, Р т о – мощность теплоотдачи. Величина отдачи тепла пропорциональна внешней поверхности. Площадь внешней поверхности соленоида S пов = 2·p· R2 (l + R2). Площадь боковой поверхности S б пов = 2·p· R2 · l. В электротехнике принято, что температура обмоток на поверхности не должна быть выше 60˚С. Легко показать, что при таких температурах потерями мощности на тепловое излучение можно пренебречь[1]. Отсеется учесть только теплоотдачу в окружающее пространство: Р 2 = a· S повD T, где a - коэффициент теплоотдачи. Для воздуха у гладкой стенки коэффициент теплоотдачи a = 5.6 + 4 v Вт/(м2·К), где v – скорость потока воздуха. Как видно a сильно зависит от скорости воздуха. Именно это обстоятельство используется для охлаждения с помощью вентиляции. При расчет охлаждения только за счет естественной циркуляции воздуха можно принять, что скорость воздушного потока вокруг соленоида не превысит 1 м/с, что соответствует очень слабому ветру, тогда a = 9.6. В случае принудительного охлаждения с помощью вентилятора можно принять, что скорость воздуха обтекающего соленоид составит 10 м/с (сильный ветер). Тогда α = 45.6 и потери мощности при той же разности температур возрастут в несколько раз. При необходимости можно оценить температуру внутренних слоев соленоида. Мощность тепла предаваемая через обмотку составит: P 1 = l· S б пов D T/h, где h – толщина намотки, l = 384 Вт/м·К – теплопроводность меди, D T – разность температур. Расчеты обычно показывают, что обычно за счет высокой теплопроводности меди температура внутри и снаружи обмотки различаются незначительно. При эффективном охлаждении можно увеличивать плотность тока. Но для отвода выделяющегося тепла уже обдува может не хватить и тогда придется прокачивать через обмотку соленоида большое количество воды. При расчетах можно принять, что температура втекающей воды из водопровода будет 15˚С, а вытекающей воды 60˚С. Ежесекундно в объеме должна поглощаться мощность Р в = Р э; Р в = с · m водΔ t, где Δ t = 45˚С, с = 4200 Дж/(кг·К) – теплоемкость воды. Отсюда прямо можно определить массу воды, которая должна ежесекундно прокачиваться через соленоид m вод = Р э/ с ·Δ t. m вод. Зная секундный расход воды можно рассчитать диаметры трубопроводов и давление в водопроводной сети. Эти расчеты основываются на столь же простых формулах, но поскольку эта тема выходит за пределы работы, то она здесь не рассматривается. На рис 3. показан примерная конструкция соленоида с водяным охлаждением.
Рис. 3. конструкция соленоида с водяным охлаждением.
4. Измерение магнитного поля
Существует несколько методов измерения магнитного поля. Из них по крайней мере три наиболее часто применяются на практике. Это индукционный метод, метод ядерного магнитного резонанса и метод основанный на эффекте Холла. В данной работе для экспериментального исследования индукции магнитного поля на оси соленоида используют метод, основанный на явлении Холла[2].
E = vB, Djх = aE = avB. Учитывая (9.2), где I = jS = jahД, находим Djх = Здесь Rx = 1/(qn0) – постоянная Холла. Видно, что ЭДС Холла прямо пропорциональна индукции магнитного поля. Эффект Холла наблюдается во всех проводниках. Но в металла постоянная Холла мала. В работе используется полупроводниковый датчик Холла, поскольку у полупроводников концентрация n0 носителей заряда на несколько порядков меньше, чем в металлах, и соответственно во столько же раз больше возникающая ЭДС Холла. Это существенно облегчает измерения. Практически датчик Холла устроен очень просто (рис. 5). На диэлектрической подложке находится тонкая (~ 0.1 мм) пластинка из полупроводника (показано темным цветом). К пластике подведены печатные электроды (показаны серым цветом). Два электрода с узкими контактами предназначены для измерения ЭДС Холла. По двум широким пропускают ток. Размер датчика не превышает 2х2 мм. Датчики Холла широко применяются не только для измерения магнитных полей или для разного рода датчиков срабатывающих при наличии магнитного поля.
Поэтому для разных образцов датчика может иметь место небольшая остаточная разность потенциалов, которую надо учитывать при точных измерениях. Кроме того, концентрация носителей в полупроводниках сильно зависит от температуры. Соответственно от температуры будет зависеть и ЭДС Холла, что тоже является одним из недостатков этого метода. Однако подбором полупроводникового материала эту погрешность можно свести к минимуму. Следует учесть, что величина ЭДС Холла сильно зависит от ориентации датчика относительно силовых линий поля. Максимальная ЭДС будет при строго перпендикулярной ориентации датчика относительно силовых линий поля. Так как линии индукции магнитного поля на оси соленоида направлены вдоль оси, то датчик Холла располагается на торце специального штока.
5. Измеритель магнитной индукции Ш1-8
Назначение ручек измерителя Ш1-8. 1 – Индикатор баланса. 2 – Тумблер "Грубо-Точно" индикатора. 3 – Переключатель "Полярность". 4 – Переключатель "Отсчет индукции Т" с непосредственной индикацией измеряемого поля.
Порядок работы с прибором Ш1-8. До начала измерений переключатель "Грубо-Точно" установить в положение "Грубо". Включить прибор тумблером "Сеть". Переключая ручки "Отсчет индукции" на передней панели прибора установить нулевое значение индукции поля. Переключить Тумблер "Грубо-Точно" прибор в положение "Точно". Стрелка прибора должна находиться на нуле. Поскольку прибор чувствует поле Земли, то стрелка может находиться вблизи нуля. Если стрелка отклоняется от нуля значительно, то следует откорректировать нуль прибора или установить правильное значение на шкале "Коррекция Т". Для этого обратитесь к преподавателю. Если в отсутствии поля стрелка находится вблизи нуля, то прибор готов к измерениям. Прежде чем включать поле и помещать щуп в магнитное поле снова переключите тумблер "Грубо-Точно" в положение "Грубо". В магнитном поле стрелка должна отклониться вправо. Если стрелка отклонилась влево переключить тумблер "N-S". Теперь поворачивая переключатели "Отсчет индукции Т" выведите стрелку на нуль. Для повышения точности измерения переключить тумблер "Грубо-Точно" в положение "Точно". Окончательно добиться ручками "Отсчет индукции Т" нулевых показаний прибора. В этом случае цифры над переключателями указывают значение поля в теслах. Обратите внимание, что крайний левый переключатель "Отсчет индукции Т" определяет диапазон измерения. При измерении поля соленоида его положении должно быть "0.0".
Практическая часть
Приборы и оборудование Установка включает в себя следующие блоки: источник питания соленоида, измеритель магнитной индукции Ш1-8 с датчиком Холла на щупе, подставка для щупа, вольтметр, миллиамперметр.
Подготовка к выполнению практической части 1. Подключить к соленоиду источник питания, реостат, цифровой вольтметр и миллиамперметр (рис. 7). 2. Ознакомиться с порядком работы с измерителем магнитного поля Ш1-8. Включить измеритель поля и проверить начальную калибровку прибора (раздел 5). 3. Подготовить Ш1-8 к работе в составе установки, установив щуп в положение для измерений поля.
Задание 1 Измерение поля в центре соленоида Цель задания. Ознакомиться с методом измерения магнитных полей в соленоиде. Изучение зависимости поля от тока
1. С помощью линейки определите положение центра соленоида. Поместить щуп так, чтобы датчик оказался в центре соленоида. Координата z указывающая положение датчика Холла устанавливается по шкале на щупе датчика (рис. 7). 2. Включить источник питания. 3. Установить реостат в положение максимального тока. Измерить поле в центре соленоида. Полученный результат записать. Измерить и записать значения тока и напряжения. 4. Уменьшая ток с помощью реостата измерить величину поля при разных значениях I с. Измерения провести не менее чем для 5 значений тока в диапазоне от максимального тока до минимального значении тока. 5. Используя известную вам программу работы с графиками (Origen, SciDAVis) построить зависимость поля от тока. Аппроксимировать полученный график прямой линией. В пакете Origen уравнение прямой линии записывается в обозначениях: Y = A + B·X. Параметр В или тангенс угла наклона прямой линии даст величину пропорциональную произведению μ0· n (1.2). В приближении бесконечного соленоида определить n – число витков на единицу длины. 6. Сделать выводы о зависимости поля в соленоиде от тока и о возможных причинах отклонения от уравнения вида Y = B·X.
Задание 2 Исследование распределения поля соленоида Цель задания. Измерить распределение магнитного поля на оси соленоида.
1. Установить максимальный ток. Поместить щуп в соленоид полностью, так чтобы датчик выдвинулся наружу до первой риски (рис. 7). В этом случае датчик будет измерять поле вне соленоида на расстоянии 7 см от левого на рис. 7 торца соленоида. Измерить величину поля. Значение поля и координаты записать. 2. Перемещая щуп с датчиком вдоль оси соленоида измерить зависимость индукции в соленоиде с интервалом D z = 1 см. Отчеты производить по рискам, ориентируясь по правому торцу соленоида (рис. 7) Примечание. Вблизи центра соленоида поле меняется слабо, и перемещать щуп можно сразу на 2 или 3 см. Измерения завершить, когда датчик окажется на расстоянии 7 см перед соленоидом (справа на рис. 7). 3. Результаты всех измерений занести в таблицу. Используя известную вам программу работы с графиками построить зависимость поля вдоль оси соленоида. 4. По данным определите область однородного поля в приближении, когда поле отличается от поля в центре на 1%, 5%, 10%.
Задание 3 Расчет числа витков соленоида В задании предлагается выполнить расчет соленоида при условии, когда экспериментально измерена величина поля, но число витков неизвестно. Цель задания. Изучить методы расчета соленоидов. Произвести расчет числа витков соленоида. 1. С помощью линейки с точностью до миллиметра измерить L длину намотки соленоида. Рассчитать число витков в слое: N слоя = L / d. Диаметр провода обмотки d = 1 мм. 2. Считая что внешний диаметр соленоида D в = 8 см, а внутренний предварительно считать равным D вн = 5 см определить число слоев намотки: N с = ½(D в - D вн)/ d. 3. Найти предполагаемое число витков соленоида N = N слоя· N с. Зная полное число витков, определить число витков на единицу длины соленоида. Сравнить с полученным значением в задании 1. 4. Пользуясь выражением (1.9) рассчитать величину магнитного поля соленоида для значения тока, которое использовалось в задании 1. Обратите внимание, что в (1.9) входит полудлина соленоида и средний радиус намотки. Определите эти величины. 5. Сравнить с экспериментальным значением поля в центре соленоида. Сделать выводы о возможных причинах расхождения между расчетом и экспериментом. 6.
Задание 4 Измерение сопротивления соленоида и расчет числа витков
1. Используя результат измерения напряжения и тока, полученные в Задании 1, рассчитать по закону Ома сопротивление соленоида. 2. Исходя из величины сопротивления Rом, вычислить длину провода. Длина провода определяется так: l r = Rом · S /ρ, где S = π d 2/4 - сечение провода, ρ = 0,017 Ом·мм2/м. Примечание. Исходя из размерности ρ при расчете d берется в мм2, при этом l – получится в метрах. 3. Пользуясь методикой приведенной в разделе 2 (1.10) определить длину провода в одном вертикальном слое намотке L в c. 4. Вычислить полную длину провода. l = L в c N слоя 5. Сравнить расчетную длину l с той, что получилась в результате расчета на основании измерений сопротивления намотки (l r). Предположив, что расхождение связано с ошибкой определения внутреннего диаметра намотки, варьируя внутренний диаметр намотки, добейтесь совпадения значений длины провода определяемой путем расчета и путем измерения сопротивления. Таким образом, можно определить истинный внутренний диаметр намотки и реальное число слоев намотки. 6. Исходя из полученного значения внутреннего диаметра и методики приведенной в пункте 2 Задание 3, найти число слоев намотки. Окончательно рассчитать полное число витков соленоида.
Задание 5 Расчет распределения поля в соленоиде Цель задания. Рассчитать теоретическую зависимость поля вдоль оси соленоида и сравнить с результатами эксперимента.
1. По формулам (1.6 – 1.8) рассчитать теоретическую зависимость поля в соленоиде от координаты z. При расчете использовать значение тока такое же, как и в опыте, а также определенные ранее геометрические размеры и число витков. 2. По данным Задания 2 на одном графике постройте экспериментальную и теоретическую зависимости поля от координаты z. 3. Рассчитайте абсолютное и относительное отклонение теоретического значения поля от экспериментального DВ и DВ/В в трех точках: в центре, у одного из торцов и в крайней точке вне соленоида.
Примечание: Все расчеты для данной работы удобно проводить в пакете Mathcad.
Литература
1. Физические величины: Справочник/ А.П. Бабичев, и др. Под ред. И.С. Григорьева, Е.З. Михайлова. – М.: Энергоатомиздат. – 1991. – 1232с. 2. Кухлинг Х. Справочник по физике. М.: "МИР". – 1982. – 519с. [1] По закону Стефана – Больцмана мощность Р т и теплового излучения с поверхности составит: Р т и = s·e· S (T 4 – Т 4среды), где s = 5.67·10-8 Вт/(м2·К) – постоянная, e – излучательная способность, например для черной меди e = 0.78, S – площадь, Т – температура поверхности тела. Р т и = 5.67·10-8·0.78·1.5·(60-20)4 = 0.17 Вт. Например, при D T = 150˚С потери за счет излучения составит уже 33 Вт. [2] Э. Холл (амер. физ.) открыл это эффект в 1879 г. Лабораторная работа №1
Изучение и измерение магнитного поля соленоида
Цель работы: Ознакомится с различными способами получения и измерения магнитного поля. Ознакомится с простейшими инженерными расчетами источников магнитных полей. Провести измерение поля соленоида и определить его параметры.
Теория
1. Способы получения магнитных полей Существует два способа получения магнитного поля. В первом способе магнитное поле создается намагниченным веществом, именно так изготовляют постоянные магниты. В другом способе магнитное поле создается током протекающем по проводнику нужной конфигурации. Простейшим источником магнитного поля является виток с током. Поле на оси витка с током дается выражением:
здесь μ0 – магнитная проницаемость вакуума, R – радиус витка, I – ток, х – расстояние от центра витка. Поле в центре витка можно получить из предыдущего выражения:
Одиночный виток с током можно применить только для создания слабых магнитных полей. Значение магнитного поля Земли является естественным эталоном, относительно которого можно обсуждать сильные и слабые магнитные поля. Хотя поле Земли несколько меняется в зависимости от географического положения и геологических условий, но можно считать его приблизительно равным 0.5·10-4 Т или 0.5 Гс. Магнитное поле сравнимое с полем Земли можно получить с помощью витка радиусом 0.1 м при токе порядка 8 А. Катушка всего из 10 витков позволяет снизить ток в 10 раз, что позволяет без всяких технических проблем получать такие поля. Поскольку магнитные силовые линии проникают сквозь многие материалы, то при создании полей меньших или сравнимых с полем Земли требуется магнитная экранировка всей магнитной системы. В качестве магнитных экранов используют ферромагнитные материалы с высокой магнитной проницаемостью. В таких материалах магнитные силовые линии замыкаются в ферромагнетике и не проникают внутрь экранируемого объема. Создание магнитных полей, превышающих поле Земли не более чем в 100 раз, не составляет технической проблемы. Такие магнитные поля можно получить с помощью цилиндрических катушек – соленоидов или плоских катушек специальной конфигурации, например катушек Гельмгольца. Однако достижение более сильных полей с помощью катушек наталкивается на серьезные технические проблемы. Как видно из выражения (1.1) индукция поля пропорциональна току. В свою очередь сопротивление катушки растет пропорционально длине провода или приблизительно пропорционально числу витков. Соответственно для получения сильных магнитных полей требуется увеличивать ток, протекающий по катушке имеющей значительное сопротивление. Мощность выделяющаяся на обмотке согласно Р = I 2 ·R растет пропорционально квадрату тока. Существует правило: "Увеличение поля в 10 раз влечет за собой рост потребляемой мощности в 100 раз". В итоге при создании поля больше 0.1 Т выделяемое в катушке тепло становиться столь значительным, что требуется принудительное охлаждение. Обычно эта проблема решается путем покачивания через соленоид охлаждающей воды. Но и на этом пути возникают технические трудности. Соленоиды, предназначенные для получения полей от единиц до десятков тесла, потребляют от десятков до тысяч мегаватт мощности. Самые сильные источники поля являются уникальными сооружениями и применяются только в нескольких лабораториях в мире. Поскольку потребляемая мощность сравнима с энергопотреблением небольшого города. Для намотки можно воспользоваться сверхпроводящим проводом, сопротивление, которого при низких температурах равно нулю. В замкнутой накоротко катушке из сверхпроводящего провода может циркулирующий ток, который будет "вечно" создавать сильное поле без всяких затрат энергии. Однако очень сильные магнитные поля разрушают сверхпроводимость. Поэтому сверхпроводники обычно используют для создания полей в диапазоне до 10 Т. Но их применение зачастую ограничено из-за необходимости использования жидкого гелия. Частным методом для получения сверхсильных магнитных полей является импульсная генерация магнитного поля в небольших по размерам катушках. Но создаваемые таким способом поля существуют очень ограниченное время - обычно меньше долей секунды. Хотя этого часто оказывается достаточным для проведения научных исследований. Для создания магнитных полей больше 0.1 Т часто используют комбинацию катушки и сердечника из ферромагнитных материалов. По этому принципу устроены электромагниты. По сравнению с соленоидом электромагнит потребляет в десятки раз меньше мощность. Но электромагниты становятся столь же неэкономичными и громоздкими сооружениями, когда требуется получить поле, превышающее поле насыщения железа. По этой причине электромагниты редко применяются для создания поля большего, чем 2 Т. Постоянные магниты также применяются для создания магнитных полей. Особенно в тех случаях, когда поле не требуется изменять в пределах больших нескольких процентов от номинала. Магниты на основе традиционных сплавов ферромагнитных материалов, таких как железо, кобальт никель, не позволяют создать поля большие, чем 0.8 Т. Только магниты, в составе которых применяются редкоземельные элементы, такие как самарий или неодим позволяют получить поля до 1 Т.
2. Индукция магнитного поля соленоида Как известно из общей физики поле созданное в бесконечном соленоиде можно определить из следующего выражения: В = m0 I · n, (1.2) где I ток в соленоиде, а п число витков на единицу длины соленоида. На практике некоторым приближением к бесконечному соленоиду будет длинная катушка, у которой диаметр в несколько раз меньше длины. Очевидно, что поле внутри соленоида конечной длины будет изменяться вдоль оси катушки, достигая максимума вблизи середины и плавно уменьшаясь к торцам. Легко понять, что у торца полубесконечного соленоида магнитное поле будет в два раза меньше, чем у бесконечного соленоида. Таким образом, у длинного соленоида поле у его торцов уменьшается примерно в два раза по сравнению с полем в центре соленоида. Поэтому область однородного поля находиться только в ограниченной области вблизи центра соленоида. Если от соленоида требуется получение однородного поля большого объема, то его стремятся максимально приблизить к бесконечному соленоиду. Чтобы получить достаточно большую однородную область, диаметр катушки и отношение длины к диаметру следует выбирать возможно большими (например, порядка 3: 1). Однако, вследствие вытянутой формы соленоида доступ к рабочей области неудобен; поэтому соленоиды применимы не для всяких видов магнитных измерений. Падение напряженности магнитного поля вдоль оси соленоида можно уменьшить, увеличивая число витков на концах катушки, или располагая там дополнительные обмотки. Для получения большей однородности вдоль оси можно даже ослабить поле в середине, используя для этого вторую обмотку.
Получим выражение для магнитного поля соленоида конечной длины (рис. 1). Пусть число витков на единицу длины n и участок dz содержит n · dz витков, которые, согласно выражению (1.1) для поля витка с током, в точке на оси соленоида создадут индукцию
здесь r = (R 2 + x 2)½. Из рис. 1 видно, что
Подставляя (1.4) в (1.3) и интегрируя полученное выражение от q1 до q2, имеем
В случае бесконечного соленоида q1 ® 0, q2 ® p, и мы получим (1.2) В z = m 0 I · n. Чтобы для расчетов магнитного поля в этой работе можно было воспользоваться геометрическими размерами соленоида, выразим значения косинусов входящие в выражение (1.5). Учтем, что cosq2 = cos(180 – q3) = – cosq3 (рис. 1), тогда
Начало координат поместим в центр соленоида и обозначим
получим:
Из выражения (1.6) можно рассчитать поле в любой точке на оси соленоида, как внутри, так и вне соленоида. Для этого необходимо знать длину соленоида L, радиус R, ток I, число витков на единицу длины n и задать расстояние z от центра соленоида. Необходимо только вычислить косинусы углов q1 и q2.Надо учитывать, что выражения (1.5, 1.6) строго применимы только для однослойного соленоида. Однако в случае, когда толщина обмотки соленоида меньше его радиуса они также применимы. В этом случае число витков на единицу длины определяется как n = N / L, где N – полное число витков. Кроме того, в выражения (1.8) должен войти средний радиус намотки.
Для поля в центре z = 0 и выражения (1.7) и (1.8) упрощаются: θ1 = θ3 = θ0 и cos θ1 = – cos θ3 Соответственно В = m0 I · n ·cosθ0. Как видно отличие от формулы для бесконечного соленоида выражается только в геометрическом множителе: К = cosθ0. Для расчета геометрических множителей удобно прейти к половинной длине соленоида. Обозначим L /2 = l. Здесь l полудлина соленоида. Тогда а = b = l и К = l /(R 2 + l 2)1/2. Окончательно получим:
В = m0 I · n · l /(R 2 + l 2)1/2, (1.9)
где l – половина длины соленоида, в качестве R – обычно принимается средний радиус намотки. Однако точные формулы учитывающие толщину намотки выглядят более сложными. В рамках этой работы они не рассматриваются. 3. Порядок расчета соленоида Предположим, что величина поля в соленоиде задана. Для оценочного расчета можно применить формулу (1.2) для бесконечного соленоида, откуда определяется произведение тока на число витков на единицу длины. Дальнейший расчет сводиться к разделению в этом произведении величины тока и количества витков. А также уточнения всех геометрических величин для реального соленоида. Обычно известен размер объектов, которые будут подвергаться воздействию поля. Геометрический размер объектов определяет минимальный диаметр соленоида и требуемый объем однородного поля. Исходя из протяженности области однородного поля, можно выбрать минимальную длину соленоида, руководствуясь теоретическим выражением распределения поля вдоль оси z (1.6). В первом приближении можно положить, что длина соленоида должна быть втрое больше радиуса. Можно показать, что в этом случае поле в центре реального соленоида будет на 3% меньше поля в бесконечном соленоиде, а протяженность области однородного поля будет порядка диаметра соленоида. Пусть из этих соображений получено, что R 1 – радиус внутреннего отверстия и первого слоя витков соленоида, а L – длина соленоида. При расчете соленоида, обмотка которого намотана медным проводом, следует учитывать её разогрев при протекании тока. При прохождении тока по проводам, имеющим свободный отвод тепла, например длинные провода в воздухе или в стенах зданий, допустимая плотность тока может достигать 7 - 10 А/мм2. Поскольку соседние витки разогревают друг друга, и тепло не успевает рассеяться, то для плотной многослойной намотки допускается меньшая плотность тока. В отсутствии принудительного охлаждения обычно выбирают плотность тока j = 2 – 3 А/мм2. При большой плотности тока соленоид просто перегреется и его обмотка сгорит. При дальнейшем расчете необходимо задаться неким параметром, который выбирают из практических соображений. Часто таковым является диаметр провода. Если выбирают диаметр провода d, то его сечение S = π d 2/4. В свою очередь I = j·S. Тогда подставив выражение для тока в (1.2) получим цепочку выражений: B = μ0 j·S·n. В свою очередь число витков на единицу длины n = N/L, где L – длина соленоида, N – общее число витков. Тогда требуемое для получения заданного поля число витков определиться из выражения: N = B·L /μ0 j·S. С другой стороны число витков, которые поместятся на длине соленоида при однослойной намотке N слоя = L / d. Если окажется, что N > N слоя, то число слоев определиться N / N слоя. Теперь можно оценить толщину намотки: h = N · d / N слоя. Поскольку ранее уже был определен минимальный радиус обмотки, то можно оценить габариты соленоида. Его наибольший радиус будет R 1+ h. Если окажется, что средний радиус обмотки R 1+ h /2 таков, что выбранное соотношение длины и радиуса соленоида не удовлетворяет требованию получения нужной однородности поля, то потребуется увеличить длину, с тем чтобы уменьшить число слоев намотки и средний радиус соленоида. Приведенных расчетов не достаточно, поскольку необходимо увязать их с параметрами источника питания. Из закона Ома I·R ом = U, где U напряжение источника тока, R ом – сопротивление соленоида. Если выбрать тонкий провод, то сопротивление обмотки R ом = ρ·l/S, где l – длина провода в катушке, а ρ – удельное сопротивлении меди (ρ = 0.017 Ом·мм2/м), окажется слишком большим и для питания соленоида потребуется высоковольтный источник. На практике это по многим соображениям неудобно. Поэтому стараются выбрать провод большего сечения, чтобы сделать общее сопротивление обмотки минимальным. С таким расчетом, чтобы уложиться в параметры уже имеющегося промышленного источника питания или не выйти за пределы напряжения нескольких сотен вольт. Для расчета сопротивления требуется определить реальную длину провода. Наиболее просто длина провода может быть оценена для соленоида, у которого намотано не больше нескольких слоев провода. Тогда можно считать, что в среднем длина провода в одном витке определиться: l витка = 2π·R сол, здесь R сол средний радиус обмотки. В каждом слое поместиться N слоя = L / d. Тогда полная длина провода определиться l провода = l витка N слоя. Таким образом, зная предполагаемые геометрические размеры соленоида, и задавшись сечением провода можно найти сопротивление обмотки и определить параметры источника питания. Для многослойной намотки воспользоваться приведенной выше методикой нельзя. Требуется точно рассчитать длину провода в вертикальном слое при спиральной намотке (рис. 2). Длина провода в пределах узкого кольца шириной d r составит d L вс = 2p· r ·d r / d, где d диаметр провода, а 1/ d – число витков на единицу толщины. L в с = R1∫R22p· r ·d r / d = p·(R 22 – R 12)/ d.
Длина спиральной намотки определяется по формуле: L в с = p·(R 22 – R 12)/ d (1.10) где R 2 и R 1 соответственно наружный и внутренний радиусы, а d – диаметр провода. Тогда полная длина провода составит l провода = L в с · N слоя. Сопротивление провода такой длины составит R ом= ρ · l провода/ S. Попутно можно определить и массу медного провода m = ηCu· l провода· S, здесь плотность меди ηCu = 8960 кг/м3. Зная ток и напряжение необходимо определить максимальную мощность Р = I·U. Если окажется, что потребляемая соленоидом мощность превышает 1 кВт, то потребуется провести тепловые расчеты, с тем чтобы выяснить потребуется ли принудительное охлаждение магнитной системы.
Имеет место уравнение теплового баланса: Р э = Р т и + Р т о, где Р э – электрическая мощность подводимая к соленоиду, Р т и – мощность теплового излучения, Р т о – мощность теплоотдачи. Величина отдачи тепла пропорциональна внешней поверхности. Площадь внешней поверхности соленоида S пов = 2·p· R2 (l + R2). Площадь боковой поверхности S б пов = 2·p· R2 · l. В электротехнике принято, что температура обмоток на поверхности не должна быть выше 60˚С. Легко показать, что при таких температурах потерями мощности на тепловое излучение можно пренебречь[1]. Отсеется учесть только теплоотдачу в окружающее пространство: Р 2 = a· S повD T, где a - коэффициент теплоотдачи. Для воздуха у гладкой стенки коэффициент теплоотдачи a = 5.6 + 4 v Вт/(м2·К), где v – скорость потока воздуха. Как видно a сильно зависит от скорости воздуха. Именно это обстоятельство используется для охлаждения с помощью вентиляции. При расчет охлаждения только за счет естественной циркуляции воздуха можно принять, что скорость воздушного потока вокруг соленоида не превысит 1 м/с, что соответствует очень слабому ветру, тогда a = 9.6. В случае принудительного охлаждения с помощью вентилятора можно принять, что скорость воздуха обтекающего соленоид составит 10 м/с (сильный ветер). Тогда α = 45.6 и потери мощности при той же разности температур возрастут в несколько раз. При необходимости можно оценить температуру внутренних слоев соленоида. Мощность тепла предаваемая через обмотку составит: P 1 = l· S б пов D T/h, где h – толщина намотки, l = 384 Вт/м·К – теплопроводность меди, D T – разность температур. Расчеты обычно показывают, что обычно за счет высокой теплопроводности меди температура внутри и снаружи обмотки различаются незначительно. При эффективном охлаждении можно увеличивать плотность тока. Но для отвода выделяющегося тепла уже обдува может не хватить и тогда придется прокачивать через обмотку соленоида большое количество воды. При расчетах можно принять, что температура втекающей воды из водопровода будет 15˚С, а вытекающей воды 60˚С. Ежесекундно в объеме должна поглощаться мощность Р в = Р э; Р в = с · m водΔ t, где Δ t = 45˚С, с = 4200 Дж/(кг·К) – теплоемкость воды. Отсюда прямо можно определить массу воды, которая должна ежесекундно прокачиваться через соленоид m вод = Р э/ с ·Δ t. m вод. Зная секундный расход воды можно рассчитать диаметры трубопроводов и давление в водопроводной сети. Эти расчеты основываются на столь же простых формулах, но поскольку эта тема выходит за пределы работы, то она здесь не рассматривается. На рис 3. показан примерная конструкция соленоида с водяным охлаждением.
Рис. 3. конструкция соленоида с водяным охлаждением.
4. Измерение магнитного поля
Существует несколько методов измерения магнитного поля. Из них по крайней мере три наиболее часто применяются на практике. Это индукционный метод, метод ядерного магнитного резонанса и метод основанный на эффекте Холла. В данной работе для экспериментального исследования индукции магнитного поля на оси соленоида используют метод, основанный на явлении Холла[2].
E = vB, Djх = aE = avB. Учитывая (9.2), где I = jS = jahД, находим Djх = Здесь Rx = 1/(qn0) – постоянная Холла. Видно, что ЭДС Холла прямо пропорциональна индукции магнитного поля. Эффект Холла наблюдается во всех проводниках. Но в металла постоянная Холла мала. В работе используется полупроводниковый датчик Холла, поскольку у полупроводников концентрация n0 носителей заряда на несколько порядков меньше, чем в металлах, и соответственно во столько же раз больше возникающая ЭДС Холла. Это существенно облегчает измерения. Практически датчик Холла устроен очень просто (рис. 5). На диэлектрической подложке находится тонкая (~ 0.1 мм) пластинка из полупроводника (показано темным цветом). К пластике подведены печатные электроды (показаны серым цветом). Два электрода с узкими контактами предназначены для измерения ЭДС Холла. По двум широким пропускают ток. Размер датчика не превышает 2х2 мм. Датчики Холла широко применяются не только для измерения магнитных полей или для разного рода датчиков срабатывающих при наличии магнитного поля.
Поэтому для разных образцов датчика может иметь место небольшая остаточная разность потенциалов, которую надо учитывать при точных измерениях. Кроме того, концентрация носителей в полупроводниках сильно зависит от температуры. Соответственно от температуры будет зависеть и ЭДС Холла, что тоже является одним из недостатков этого метода. Однако подбором полупроводникового материала эту погрешность можно свести к минимуму. Следует учесть, что величина ЭДС Холла сильно зависит от ориентации датчика относительно силовых линий поля. Максимальная ЭДС будет при строго перпендикулярной ориентации датчика относительно силовых линий поля. Так как линии индукции магнитного поля на оси соленоида направлены вдоль оси, то датчик Холла располагается на торце специального штока.
5. Измеритель магнитной индукции Ш1-8
Назначение ручек измерителя Ш1-8. 1 – Индикатор баланса. 2 – Тумблер "Грубо-Точно" индикатора. 3 – Переключатель "Полярность". 4 – Переключатель "Отсчет индукции Т" с непосредственной индикацией измеряемого поля.
Порядок работы с прибором Ш1-8. До начала измерений переключатель "Грубо-Точно" установить в положение "Грубо". Включить прибор тумблером "Сеть". Переключая ручки "Отсчет индукции" на передней панели прибора установить нулевое значение индукции поля. Переключить Тумблер "Грубо-Точно" прибор в положение "Точно". Стрелка прибора должна находиться на нуле. Поскольку прибор чувствует поле Земли, то стрелка может находиться вблизи нуля. Если стрелка отклоняется от нуля значительно, то следует откорректировать нуль прибора или установить правильное значение на шкале "Коррекция Т". Для этого обратитесь к преподавателю. Если в отсутствии поля стрелка находится вблизи нуля, то прибор готов к измерениям. Прежде чем включать поле и помещать щуп в магнитное поле снова переключите тумблер "Грубо-Точно" в положение "Грубо". В магнитном поле стрелка должна отклониться вправо. Если стрелка отклонилась влево переключить тумблер "N-S". Теперь поворачивая переключатели "Отсчет индукции Т" выведите стрелку на нуль. Для повышения точности измерения переключить тумблер "Грубо-Точно" в положение "Точно". Окончательно доби
|

 , (1.1)
, (1.1) .
. , (1.3)
, (1.3) ,
,  . (1.4)
. (1.4) (cosq1 – cosq2). (1.5)
(cosq1 – cosq2). (1.5) . (1.6)
. (1.6)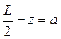 ,
,  , (1.7)
, (1.7) и
и  . (1.8)
. (1.8)
 Потери тепла с поверхности соленоида происходят за счет теплоотдачи и теплового излучения. В условиях теплового равновесия мощность выделяющаяся в обмотке соленоида должна равняться мощности излучаемой с внешней поверхности.
Потери тепла с поверхности соленоида происходят за счет теплоотдачи и теплового излучения. В условиях теплового равновесия мощность выделяющаяся в обмотке соленоида должна равняться мощности излучаемой с внешней поверхности.
 Рассмотрим проводящую пластину с поперечным сечением ahД и плотностью тока j, поместив ее в поперечное магнитное поле с индукцией В (рис. 4). Явление Холла состоит в том, что в проводящей пластинке по которой протекает ток и которая находится в магнитном поле перпендикулярно плоскости, в которой лежат векторы В и j, образуется электрическое поле с напряженностью Е. В результате между боковыми гранями возникает разность потенциалов, равная Djх= Еа, которая и называется ЭДС Холла. Физическая природа явления Холла может быть сведена к действию силы Лоренца (9.19), а точнее, ее магнитной составляющей q [ v, В ]. Под действием этой силы носители тока смещаются к боковой грани пластинки. У противоположной грани образуется избыточный заряд противоположного знака, связанный с решеткой. Между положительным и отрицательным зарядами, т. е. между боковыми гранями пластины, и образуется ЭДС Холла Djх. Ее значение можно найти из условия равновесия между силой Лоренца и возникающей электрической силой: FЛ = FE,или qvВ=qЕ, откуда
Рассмотрим проводящую пластину с поперечным сечением ahД и плотностью тока j, поместив ее в поперечное магнитное поле с индукцией В (рис. 4). Явление Холла состоит в том, что в проводящей пластинке по которой протекает ток и которая находится в магнитном поле перпендикулярно плоскости, в которой лежат векторы В и j, образуется электрическое поле с напряженностью Е. В результате между боковыми гранями возникает разность потенциалов, равная Djх= Еа, которая и называется ЭДС Холла. Физическая природа явления Холла может быть сведена к действию силы Лоренца (9.19), а точнее, ее магнитной составляющей q [ v, В ]. Под действием этой силы носители тока смещаются к боковой грани пластинки. У противоположной грани образуется избыточный заряд противоположного знака, связанный с решеткой. Между положительным и отрицательным зарядами, т. е. между боковыми гранями пластины, и образуется ЭДС Холла Djх. Ее значение можно найти из условия равновесия между силой Лоренца и возникающей электрической силой: FЛ = FE,или qvВ=qЕ, откуда . (1.14)
. (1.14) При отсутствии поля ЭДС Холла равна нулю в том случае если измерительные электроды присоединены строго на одной эквипотенциальной поверхности, что часто затруднительно реализовать на практике.
При отсутствии поля ЭДС Холла равна нулю в том случае если измерительные электроды присоединены строго на одной эквипотенциальной поверхности, что часто затруднительно реализовать на практике. Измерение магнитной индукции в измерителе Ш1-8 производится с использованием датчика Холла (рис. 6). Прибор относится к разновидности приборов работающих по принципу сравнения измеряемой величины (ЭДС Холла) с эталонным напряжением. Величина эталонного напряжения задается многопредельным переключателем с непосредственным отображением результата измерения.
Измерение магнитной индукции в измерителе Ш1-8 производится с использованием датчика Холла (рис. 6). Прибор относится к разновидности приборов работающих по принципу сравнения измеряемой величины (ЭДС Холла) с эталонным напряжением. Величина эталонного напряжения задается многопредельным переключателем с непосредственным отображением результата измерения.
 , (1.1)
, (1.1)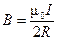 .
. , (1.3)
, (1.3) ,
,  . (1.4)
. (1.4) (cosq1 – cosq2). (1.5)
(cosq1 – cosq2). (1.5) . (1.6)
. (1.6) ,
, 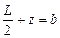 , (1.7)
, (1.7) и
и  . (1.8)
. (1.8)
 Потери тепла с поверхности соленоида происходят за счет теплоотдачи и теплового излучения. В условиях теплового равновесия мощность выделяющаяся в обмотке соленоида должна равняться мощности излучаемой с внешней поверхности.
Потери тепла с поверхности соленоида происходят за счет теплоотдачи и теплового излучения. В условиях теплового равновесия мощность выделяющаяся в обмотке соленоида должна равняться мощности излучаемой с внешней поверхности.
 Рассмотрим проводящую пластину с поперечным сечением ahД и плотностью тока j, поместив ее в поперечное магнитное поле с индукцией В (рис. 4). Явление Холла состоит в том, что в проводящей пластинке по которой протекает ток и которая находится в магнитном поле перпендикулярно плоскости, в которой лежат векторы В и j, образуется электрическое поле с напряженностью Е. В результате между боковыми гранями возникает разность потенциалов, равная Djх= Еа, которая и называется ЭДС Холла. Физическая природа явления Холла может быть сведена к действию силы Лоренца (9.19), а точнее, ее магнитной составляющей q [ v, В ]. Под действием этой силы носители тока смещаются к боковой грани пластинки. У противоположной грани образуется избыточный заряд противоположного знака, связанный с решеткой. Между положительным и отрицательным зарядами, т. е. между боковыми гранями пластины, и образуется ЭДС Холла Djх. Ее значение можно найти из условия равновесия между силой Лоренца и возникающей электрической силой: FЛ = FE,или qvВ=qЕ, откуда
Рассмотрим проводящую пластину с поперечным сечением ahД и плотностью тока j, поместив ее в поперечное магнитное поле с индукцией В (рис. 4). Явление Холла состоит в том, что в проводящей пластинке по которой протекает ток и которая находится в магнитном поле перпендикулярно плоскости, в которой лежат векторы В и j, образуется электрическое поле с напряженностью Е. В результате между боковыми гранями возникает разность потенциалов, равная Djх= Еа, которая и называется ЭДС Холла. Физическая природа явления Холла может быть сведена к действию силы Лоренца (9.19), а точнее, ее магнитной составляющей q [ v, В ]. Под действием этой силы носители тока смещаются к боковой грани пластинки. У противоположной грани образуется избыточный заряд противоположного знака, связанный с решеткой. Между положительным и отрицательным зарядами, т. е. между боковыми гранями пластины, и образуется ЭДС Холла Djх. Ее значение можно найти из условия равновесия между силой Лоренца и возникающей электрической силой: FЛ = FE,или qvВ=qЕ, откуда . (1.14)
. (1.14) При отсутствии поля ЭДС Холла равна нулю в том случае если измерительные электроды присоединены строго на одной эквипотенциальной поверхности, что часто затруднительно реализовать на практике.
При отсутствии поля ЭДС Холла равна нулю в том случае если измерительные электроды присоединены строго на одной эквипотенциальной поверхности, что часто затруднительно реализовать на практике. Измерение магнитной индукции в измерителе Ш1-8 производится с использованием датчика Холла (рис. 6). Прибор относится к разновидности приборов работающих по принципу сравнения измеряемой величины (ЭДС Холла) с эталонным напряжением. Величина эталонного напряжения задается многопредельным переключателем с непосредственным отображением результата измерения.
Измерение магнитной индукции в измерителе Ш1-8 производится с использованием датчика Холла (рис. 6). Прибор относится к разновидности приборов работающих по принципу сравнения измеряемой величины (ЭДС Холла) с эталонным напряжением. Величина эталонного напряжения задается многопредельным переключателем с непосредственным отображением результата измерения.


