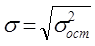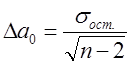под корреляцией – определение тесноты связи изучаемых признаков.
1. Для построения регрессионной модели надо иметь достаточно большое количество единиц анализируемой совокупности (не менее 50). 2. Распределение показателей, включенных в модель должно быть близким к нормальному, т.е. сила вариации каждого фактора должна быть незначительной.
В 2. Этапы корреляционно-регрессионного анализа: 1. Предварительный (априорный) анализ. Он дает неплохие результаты если проводится достаточно квалифицированным исследователем. 2. Сбор информации и ее первичная обработка. Здесь выявляются ошибки, информация проверяется на нормальность распределения, иногда проводят группировку для предварительного установления связей. 3. Построение модели (уравнения регрессии). Как правило эту процедуру выполняют на ПК используя стандартные программы. 4. Оценка тесноты связей признаков, оценка уравнения регрессии и анализ модели. 5. Прогнозирование развития анализируемой системы по уравнению регрессии. На первом этапе формулируется задача исследования, определяется методика измерения показателей или сбора информации, исключаются дублирующие факторы или связанные в жестко-детерминированную систему. На втором этапе анализируется объем единиц: совокупность должна быть достаточно большой по числу единиц и наблюдений(N>>50), число факторов "n" должно соответствовать количеству наблюдений "N". Данные должны быть количественно и качественно однородны. На третьем этапе определяется внешний вид аналитической функции и находятся ее параметры. На четвертом этапе оценивается достоверность всех характеристик корреляционной связи и уравнения регрессии. На пятом этапе осуществляется прогноз показателей, включенных в модель. Здесь выбираются наилучшие и наихудшие значения факторов и результата. По модели возможно осуществить ранжир единиц совокупности, отражающий эффективность использования ими факторов, включенных в уравнение регрессии.
В 3. К самым простым корреляционным связям относят парные или однофакторные связи. Среди парных выделяют: линейные и криволинейные связи. Для их могут быть использованы следующие уравнения регрессии: 1. Линейное уравнение регрессии:
2. Степенная связь:
или
Это уравнение может быть приведено к линейному логарифмированием: log Y = log a + b log x 3. Показательная связь:
Уравнение приводится к линейному виду: log Y = log a +(log b) x 4. Гипербола:
Это уравнение преобразуется в линейное подстановкой величины, обратной x, т.е.
тогда 5. Парабола:
3. Процесс построения регрессионной модели сводится к осреднению результата и факторов. Пусть исходные данные "x" и "y" сведены в таблицу.
S Для парной связи можно построить точечную диаграмму на основании которой можно определить вид уравнения регрессии:
... ... ... ..
Уравнение регрессии должно быть построено таким, чтобы обеспечить минимум суммы квадратов разности отклонений эмпирических значений результата от теоретических, т.е. полученных по модели:
Это достигается при использовании метода наименьших квадратов.
Получим:
a0*Sx + a1*Sx2 = SXY.
В учебниках по общей теории статистики, как правило, даются формулы для расчета а0 и а1:
где D -- главный определитель знаменателя. Эти формулы получены при решении системы уравнений через определители второго порядка (правило Крамера). В полученном уравнении регрессии параметры носят следующие названия: а0 – свободный член; а1 – коэффициент регрессии. В уравнении свободный член может иметь экономико-технологический смысл, а может не иметь. Коэффициент регрессии всегда интерпретируем. Он показывает в среднем на сколько единиц своего измерения изменится результат, если факторный показатель изменится в среднем на единицу своего измерения. Например, получено уравнение зависимости уровня рентабельности от уровня механизации производственного процесса:
а0=10% будет отражать уровень рентабельности при полном отсутствии механизации труда; а1=0,301% показывает, что уровень рентабельности увеличится на 0,3%, если уровень механизации вырастет на 1%. Имея уравнение, вычислим теоретические значения результативного показателя (см. таблицу 1).
В 5. Насколько близко фактические точки разбросаны вокруг теоретической линии регрессии, оценивают по показателям тесноты связей. 1. Парный коэффициент корреляции:
Величина (
Парный коэффициент корреляции интерпретируется в зависимости от его величины и знака. Всегда 0<r<1 или –1<r<0. Если 0<r<1, то связь факторов прямая. Если –1<r<0, то связь факторов обратная. Если r< = 0.3, то связь признаков слабая; если 0.3< │ r │ <0.7, то связь средняя; если │ r │ >=0.7, то связь сильная (или тесная). 2. Парный коэффициент детерминации: r2 * 100%. Он показывает, на сколько процентов вариация результата зависит от вариации фактора. 3. Коэффициент эластичности (Э).Коэффициент эластичности находят как первую производную:
Коэффициент эластичности результативного признака относительно факторного признака показывает, на сколько процентов изменится в среднем результат при изменении Х на 1% своего среднего значения.
6. Поскольку изучаемая совокупность по объему всегда ограничена, то значения параметров уравнения регрессии и коэффициентов корреляции и детерминации могут искажаться действием случайных факторов. Поэтому нужно с помощью какого-либо критерия достоверности оценить все показатели, т.е. подтвердить или опровергнуть нуль-гипотезу. Для линейной связи обычно используют t-критерий (Стьюдента). Определяют t расчетные для a0, a1 и r. Сравнивают полученные значения с t табличными. Если расчетные t больше t табличных, то нуль-гипотеза о недостоверности уравнения отвергается. Таким уравнением можно пользоваться для анализа и прогноза показателей.
n= n –2 -- число степеней свободы. s2ост.= s2y - s2
t табличное находим по значению n преимущественно при вероятности p=0.90; p=0.95; p=0.99. В статистике принято для каждого параметра определять доверительные интервалы. Это можно сделать, использовав коэффициент Стьюдента. ai ±t* Dai;
|



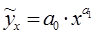
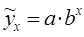


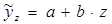 .
.








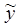 = Syx
= Syx Y ..
Y .. x
x S(y1 – y1)2 = min
S(y1 – y1)2 = min Для прямой линии Yx = a0 + a1x составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными).
Для прямой линии Yx = a0 + a1x составим линейную систему нормальных уравнений (два уравнения с двумя неизвестными). n*a0 + a1*Sx = SY,
n*a0 + a1*Sx = SY,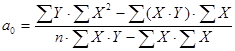


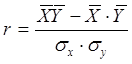


 называется ковариацией:
называется ковариацией: )= COVyx (это показатель величины совместной вариации Х и Y).
)= COVyx (это показатель величины совместной вариации Х и Y).
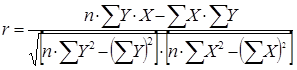




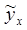 ;
;