Теоретическая часть. Крупность исходного порошка от 20 до 50 мм, температура слоя от 800 до 900 ° С
Основная реакция: NbCl5 + 2,5H2 = Nb + 5HCl (10) Крупность исходного порошка от 20 до 50 мм, температура слоя от 800 до 900 ° С. Крупность готового порошка от 200 до 400 мкм. Готовые порошки дегазируют от водорода нагреванием в вакууме или аргоне. Преимущества восстановления в печах КС – это высокая чистота получаемого металла. Лабораторная работа 3 Изучение магнитного поля на оси соленоида
Цель работы. Исследование распределения индукции магнитного поля вдоль оси соленоида. Приборы и оборудование. Генератор синусоидального тока, цифровой вольтметр, соленоид, зондовая катушка, компас.
Теоретическая часть
Рассмотрим проводник, намотанный по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Если шаг винтовой линии мал по сравнению с радиусом витка, то магнитное поле соленоида можно рассматривать как результат сложения полей, создаваемых круговыми токами, расположенными рядом и имеющими общую ось.
Рис.1. Круговой ток
Величина индукции магнитного поля в некоторой точке A на оси кругового тока
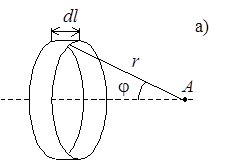
которое можно получить, воспользовавшись законом Био-Савара и принципом суперпозиции (см. Приложение), где Если соленоид имеет длину l и содержит N витков, то малая часть соленоида длиной dl (рис. 2а) содержит
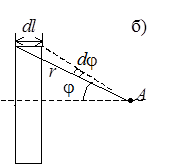
(см. рис. 2б,
где
Рис. 2. К выводу формулы (3) Интегрируя выражение (2) в пределах от j1 до p/2 (рис. 2в), получим индукцию магнитного поля в точке А 1, лежащей на торце соленоида:
Поле в произвольной точке A, лежащей на оси соленоида внутри него, может быть вычислено как сумма магнитных полей, создаваемых соленоидами C1 и C2 (рис. 2в), а в точке A ', лежащей вне соленоида, магнитное поле равно разности полей, создаваемых соленоидами С3 и С4. В результате получим
где Из выражения (3) следует, что в центре соленоида (
В случае длинного соленоида ( Формула (3) справедлива не только для постоянных i и B, но и для мгновенных значений изменяющихся во времени тока и магнитного поля, если только их изменения не происходят слишком быстро (для квазистационарных токов). В частности, если ток через соленоид меняется по закону
|


 радиуса R (рис. 1) определяется выражением
радиуса R (рис. 1) определяется выражением , (1)
, (1) - магнитная постоянная,
- магнитная постоянная,  - модуль вектора
- модуль вектора  , определяющего положение точки A.
, определяющего положение точки A. витков и может рассматриваться как круговой ток величиной
витков и может рассматриваться как круговой ток величиной 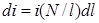 . Учитывая, что
. Учитывая, что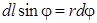
 - бесконечно малое приращение угла
- бесконечно малое приращение угла 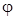 ), получим для индукции магнитного поля в точке А на оси такого "элементарного" соленоида
), получим для индукции магнитного поля в точке А на оси такого "элементарного" соленоида ,
, - число витков, приходящихся на единицу длины соленоида. Так как
- число витков, приходящихся на единицу длины соленоида. Так как 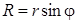 , то
, то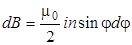 (2)
(2)


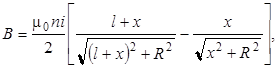 (3)
(3) 0 вне соленоида и
0 вне соленоида и 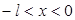 внутри соленоида (рис. 2в).
внутри соленоида (рис. 2в). ) индукция магнитного поля равна
) индукция магнитного поля равна (4)
(4)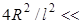 1) магнитное поле в его центральной части слабо зависит от x (
1) магнитное поле в его центральной части слабо зависит от x ( ) и начинает заметно уменьшаться лишь на расстояниях (2…3) R от торцов соленоида. На торце длинного соленоида индукция магнитного поля становится равной
) и начинает заметно уменьшаться лишь на расстояниях (2…3) R от торцов соленоида. На торце длинного соленоида индукция магнитного поля становится равной  .
.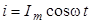 , то по такому же закону меняется и магнитное поле
, то по такому же закону меняется и магнитное поле 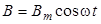 , причем амплитудные значения тока
, причем амплитудные значения тока 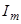 и магнитного поля
и магнитного поля  на оси соленоида связаны формулой (3), в которой
на оси соленоида связаны формулой (3), в которой  ,
,  .
.


