Проверьте выполнение предпосылок метода наименьших квадратов в исследуемой модели парной линейной регрессии.
Проверьте выполнение предпосылок метода наименьших квадратов в исследуемой модели парной линейной регрессии. Методические рекомендации Связь между Эти свойства оценок, полученных по методу наименьших квадратов, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. Для получения по методу наименьших квадратов наилучших результатов необходимо выполнение следующих предпосылок (условий Гаусса – Маркова): 1. случайный характер остатков; 2. нулевая средняя величина 3. гомоскедастичность – дисперсия каждого 4. отсутствие автокорреляции остатков. Значения остатков 5. остатки подчиняются закону нормального распределения. При выполнимости указанных предпосылок имеет место теорема Гаусса-Маркова: оценки Если какая-либо из предпосылок не выполняется, то следует корректировать модель. Проверить выполнение предпосылок метода наименьших квадратов можно с помощью следующих процедур. Для проверки первой предпосылки - случайного характера остатков Для оценки выполнения второй предпосылки необходимо определить сумму остатков. При выполнении данной предпосылки В рамках соблюдения второй предпосылки метода наименьших квадратов исследуется несмещенность оценок коэффициентов регрессии. Для этого строится график зависимости случайных остатков Если точки на графике расположены в виде горизонтальной полосы, то остатки Вторая предпосылка является «априорным» свойством фактической ошибки и всегда выполняется при использовании метода наименьших квадратов. В соответствии с третьей предпосылкой требуется, чтобы дисперсия остатков была гомоскедастичной, иначе имеет место гетероскедастичность. Визуально оценить наличие гомоскедастичности можно на основе графика зависимости остатков Для обнаружения гетероскедастичности используйте следующие тесты. Тест ранговой корреляции Спирмена позволяет проверить наиболее общие предположения о наличии гетероскедастичности. Для нахождения коэффициента ранговой корреляции Спирмена После расстановки рангов, вычисляют значение коэффициента ранговой корреляции по формуле:
где Затем следует оценить значимость рассчитанного коэффициента ранговой корреляции с помощью t-статистики.
Если Для расчета коэффициента ранговой корреляции расчеты удобнее выполнять в таблице. Таблица 7 – Расчет коэффициента ранговой корреляции Спирмена
- Тест Голдфельда-Квандта применяется, в том случае, когда есть предположение о том, что ошибки регрессии можно считать нормально распределенными случайными ошибками. Алгоритм проведения теста. 1. Упорядочить данные по убыванию значения фактора ( 2. Исключить из упорядоченной совокупности ( 3. Построить две независимые регрессии первых 4. Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью критерия Фишера. Нулевая гипотеза о равенстве дисперсий двух наборов по
Четвертой предпосылкой регрессионного анализа является независимость случайной составляющей в любом наблюдении от его значений во всех других наблюдениях. Если данное условие не выполняется, то имеет место автокорреляции, и в этом случае коэффициенты регрессии, полученные по методу наименьших квадратов, оказываются неэффективными. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Для проверки наличия корреляции первого порядка в остатках может быть использован тест Дарбина-Уотсона. По полученным остаткам модели (
Данная статистика может принимать значения в интервале [0; 4]. При отсутствии автокорреляции остатков значения статистики DW близки 2. Точнее для применения теста DW по количеству наблюдений В зависимости от значений статистики DW делается вывод о наличии автокорреляции в ряду остатков (табл.8). Таблица 8 – Характеристика статистики DW
Также коэффициент автокорреляции, характеризующий линейную зависимость между исходным рядом остатков Если значение коэффициента корреляции окажется существенно отличным от нуля, то остатки автокоррелированы. Проверку соответствия распределения остаточной последовательности нормальному закону распределения – выполнение пятой предпосылки - можно осуществить с помощью R/S-критерия, величина которого определяется по формуле:
где
Расчетное значение R/S-критерия сравнивают с табличными значениями (нижней и верхней границами) (Приложение). Если значение критерия не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается. Для проверки распределения остатков 1. Практически все отклонения остатков 2. Примерно 2/3 (67%) всех отклонений значений остатков 3. Половина всех отклонений остатков где Для определения значений среднеквадратического отклонения с помощью табличного редактора Excel можно воспользоваться статистической функцией ДИСПР, выделив соответственно интервал данных Сделайте вывод о выполнении предпосылок МНК.
|
и 
в парной регрессии является вероятностной (стохастической, корреляционной). Поэтому оценки параметров 
и 
являются случайными величинами, свойства которых существенно зависят от свойств случайной составляющей 
. Оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными.
;
. Если на графике отсутствует какая-либо направленность в распределении точек, то остатки 
. Это условие выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.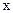
.
следует проранжировать объекты по значениям фактора 
. При этом используют прямое ранжирование (от минимального значения к максимальному), то есть минимальному значению показателя (фактора или случайной составляющей) присваивают наименьший ранг 1… Если при ранжировании невозможно найти существенные различия между значениями фактора (ошибки) по нескольким объектам, то данные объекты являются связанными. В этом случае данным объектам приписывают одинаковые средние ранги.
– разность между рангами значений 
и 
.
, то гипотеза об отсутствии гетероскедастичности отклоняется.
)
)
)
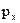) средних наблюдений, 
.
и последних 
наблюдений с помощью метода наименьших квадратов и определить соответствующие остатки 
.
наблюдениям (т.е. гипотеза об отсутствии гетероскедастичности) отвергается, если:
) и остаткам, сдвинутым на один шаг (
) вычисляется статистика Дарбина-Уотсона по формуле:
, числу объясняющих переменных 
и уровню значимости 
по таблицам Дарбина-Уотсона находится нижнее (
) и верхнее (
) значения (Приложение). Затем отрезок [0; 4] разбивается на 5 частей.
и рядом остатков, сдвинутым на один уровень 
, может быть определен по формуле линейного коэффициента парной корреляции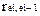 
.
- стандартное отклонение остатков модели (стандартная ошибка), которая определяется по формуле:
(99,7 %) должны быть меньше ± 
;
;
.
). И из полученного результата необходимо извлечь корень, что будет определять искомую величину среднеквадратического отклонения 
