Линейные операции над векторами.
Разум интерпретирует информацию с помощью набора устоявшихся обозначений. Душа не думает и не говорит, а чувствует и знает. Разум способен создать только относительно новую версию дома из старых кубиков. Принципиально новые открытия приходят из нереализованных секторов. Душа служит посредником между принципиально новой информацией и разумом. Душа воспринимает нереализованную информацию как знания без интерпретаций. Если разуму удается интерпретировать информацию души, рождается открытие. Разум способен однозначно определить состояние душевного комфорта. Приучите себя обращать внимание на душевный комфорт. Отказавшись от важности, вы получаете свободу выбора своей судьбы. Свобода выбора позволяет не просить, не требовать и не бороться, а пойти и взять. Структура информации организована в цепочки причинно-следственных связей. Причинно-следственные связи порождают течение вариантов. Пути наименьшего сопротивления организованы в отдельные потоки. Потоки в течении вариантов уже содержат в себе решения всех проблем. Внутренняя и внешняя важность выбрасывает разум из оптимального потока. К водопаду вас приводит разум, а не потоки в течении вариантов. Все делается гораздо проще, чем кажется. Отдайтесь этой простоте. Срабатывает не сама примета, а ваше отношение к ней. Путеводные знаки указывают на возможный поворот в течении вариантов. Линии жизни качественно отличаются друг от друга. Знаки настораживают, потому что появляются при переходе на другую линию. Знаки отличаются тем, что создают ощущение, как будто что-то не так. Спонтанные фразы можно воспринимать как руководство к действию. Состояние душевного дискомфорта является ясным знаком. Если вам приходится себя уговаривать, значит, душа говорит «нет». Если есть возможность отказаться от дискомфортного решения — отказывайтесь. Необходимо ослабить хватку и принять непредвиденное событие в свой сценарий. Принять возможность отклонения от сценария мешает важность. Разум стремится управлять не своим движением по течению, а самим течением. Перенесите центр тяжести с контроля на наблюдение. Отказавшись от контроля, вы получите подлинный контроль над ситуацией. Если вы будете двигаться по течению вариантов, мир пойдет к вам навстречу. ВЕКТОРЫ В ПРОСТРАНСТВЕ R. Изучение аналитической геометрии существенно опирается на понятие геометрического вектора. В этой главе рассматриваются операции над векторами, вводятся такие важные понятия как линейная независимость, ранг и базис системы векторов.
Геометрические векторы. Основные понятия. Определение. Геометрическим вектором или просто вектором называется направленный отрезок. Если точки Начало вектора называют точкой приложения вектора. Длину вектора Определение. Вектор, модуль которого равен единице, называют единичным вектором. Определение. Векторы В этом случае пишут Определение. Единичный вектор, одинаково направленный с вектором Вектор Определение. Вектор называется нулевым, если начало и конец этого вектора совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Определение. Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях. Определение. Векторы
В математике, как правило, изучают свободные векторы. Эти векторы определены с точностью до точки приложения. Линейные операции над векторами. Линейными операциями над векторами принято называть операцию сложения векторов и операцию умножения вектора на вещественное число. Определение. Суммой Правило сложения двух векторов, основанное на этом определении, обычно называют «правило треугольника». Правило сложения векторов обладает теми же самыми свойствами, что и правило сложения вещественных чисел: 1) 2)
4) для каждого вектора ►Для доказательства свойства 1 приложим векторы Рис. 2.1 параллелограмм
►Для доказательства свойства 2 приложим начало вектора С одной стороны
Если приложить начало каждого последующего вектора Рис. 2.2 начала вектора
Замечание. Разность векторов Рис. 2.3 Определение. Произведением вектора Докажем, что ►Действительно, Операция умножения вектора на число обладает следующими свойствами: 1) 2)
►Для доказательства свойства 1 приложим векторы
Рис. 2.4 Другие свойства очевидны.
|

 и
и  соответственно начало и конец направленного отрезка, то такой вектор обозначают
соответственно начало и конец направленного отрезка, то такой вектор обозначают  .
.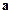 называют модулем вектора
называют модулем вектора  и обозначают
и обозначают 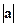 . Очевидно,
. Очевидно,  .
. называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или параллельных прямых. . Если векторы
. Если векторы  , a если векторы имеют противоположное направление, то
, a если векторы имеют противоположное направление, то  .
. .
.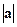 - о длине этого вектора. В дальнейшем будет показано, что
- о длине этого вектора. В дальнейшем будет показано, что  .
.
 двух векторов
двух векторов  называется вектор, идущий из начала вектора
называется вектор, идущий из начала вектора  (коммутативность);
(коммутативность); (ассоциативность);
(ассоциативность); 3) существует нулевой вектор
3) существует нулевой вектор  такой, что
такой, что  для любого вектора
для любого вектора  .
. (рис. 2.1) и рассмотрим
(рис. 2.1) и рассмотрим , где
, где ,
,  .Тогда
.Тогда  ,
, , откуда
, откуда  к концу вектора
к концу вектора 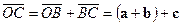 ,
, 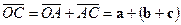 , откуда
, откуда 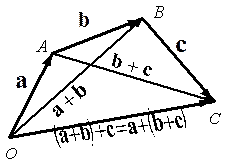 Из свойства 2 следует правило построения вектора суммы любого числа слагаемых.
Из свойства 2 следует правило построения вектора суммы любого числа слагаемых. к концу предыдущего вектора
к концу предыдущего вектора  , то вектор, идущий из
, то вектор, идущий из к концу вектора
к концу вектора  является вектором суммы
является вектором суммы  («правило многоугольника»). При
(«правило многоугольника»). При  «правило многоугольника» становится «правилом треугольника».
«правило многоугольника» становится «правилом треугольника». Определение. Разностью
Определение. Разностью  вектора
вектора  , т.е.
, т.е.  .
.
 называется вектор
называется вектор  и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора  , и противоположное вектору
, и противоположное вектору  .
. ,
, 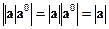 , поэтому
, поэтому  (дистрибутивность);
(дистрибутивность); (дистрибутивность);
(дистрибутивность); 3)
3)  .
. к общему началу
к общему началу  и
и  , диагональ
, диагональ равна
равна  , а диагональ
, а диагональ 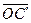 равна
равна  . Из подобия треугольников
. Из подобия треугольников  и
и  следует
следует 


