Критерии коллинеарности и компланарности векторов.
Определение. Выражение вида  , где
, где  действительные числа, называется линейной комбинацией геометрических векторов
действительные числа, называется линейной комбинацией геометрических векторов  .
.
Определение. Система геометрических векторов  называется линейно зависимой, если хотя бы один вектор этой системы может быть представлен в виде линейной комбинации других векторов этой системы.
называется линейно зависимой, если хотя бы один вектор этой системы может быть представлен в виде линейной комбинации других векторов этой системы.
В противном случае система называется линейно независимой.
Теорема 1. Два коллинеарных вектора  и
и 
 линейно зависимы
линейно зависимы
►Действительно, если  , то
, то  (знак плюс, если
(знак плюс, если  , и знак минус, если
, и знак минус, если  . Тогда
. Тогда
 , откуда следует, что
, откуда следует, что
вектор  линейно выражается через вектор
линейно выражается через вектор  , поэтому
, поэтому  и
и  линейно зависимы.◄
линейно зависимы.◄
Теорема 2. Два неколлинеарных вектора  и
и  линейно независимы.
линейно независимы.
►Предположим, что векторы  и
и  линейно зависимы. Тогда хотя бы один из этих векторов представим в виде линейной комбинации другого, например,
линейно зависимы. Тогда хотя бы один из этих векторов представим в виде линейной комбинации другого, например,  , но последнее означает, что векторы
, но последнее означает, что векторы  и
и  коллинеарны. Полученное противоречие доказывает теорему.◄
коллинеарны. Полученное противоречие доказывает теорему.◄
Из теорем 1 и 2 следует критерий коллинеарности двух векторов.
Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них может быть представлен в виде линейной комбинации другого.
 Теорема 3. Любой вектор плоскости можно разложить по двум неколлинеарным векторам, причем, единственным образом.
Теорема 3. Любой вектор плоскости можно разложить по двум неколлинеарным векторам, причем, единственным образом.
►;Пусть векторы  и
и  неколлинеарны. Приложим их к общему началу
неколлинеарны. Приложим их к общему началу  (рис.2.5).
(рис.2.5).
Рис. 2.5 Произвольный вектор  плоскости приложим к этому же началу. Из конца вектора
плоскости приложим к этому же началу. Из конца вектора  проведем прямые, параллельные векторам
проведем прямые, параллельные векторам  и
и  , и построим параллелограмм
, и построим параллелограмм  . Так как вектор
. Так как вектор 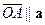 , то
, то
существует такое число  , что
, что 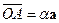 . Вектор
. Вектор  ,поэтому его можно представить в виде
,поэтому его можно представить в виде  . Тогда
. Тогда  .
.
Покажем единственность разложения  .
.
Пусть наряду с этим разложением существует и другое разложение  . Не нарушая общности можно считать, что
. Не нарушая общности можно считать, что  . Вычитая последнее равенство из предыдущего, имеем
. Вычитая последнее равенство из предыдущего, имеем  , откуда следует, что
, откуда следует, что 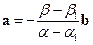 и векторы
и векторы  и
и  коллинеарны. Полученное противоречие доказывает единственность разложения.◄
коллинеарны. Полученное противоречие доказывает единственность разложения.◄
Теорема 4. Три компланарных вектора  ,
,  и
и  линейно зависимы.
линейно зависимы.
►1) Если векторы  и
и  коллинеарны, то один из этих векторов можно представить в виде линейной комбинации другого. Не нарушая общности можно считать, что
коллинеарны, то один из этих векторов можно представить в виде линейной комбинации другого. Не нарушая общности можно считать, что  . Тогда
. Тогда  и векторы
и векторы  ,
,  и
и  линейно зависимы.
линейно зависимы.
2) Если векторы  и
и  неколлинеарны, то вектор
неколлинеарны, то вектор  можно в силу теоремы 3 разложить по векторам
можно в силу теоремы 3 разложить по векторам  и
и  , т.е. представить в виде
, т.е. представить в виде  , а это означает, что данные векторы линейно зависимы.◄
, а это означает, что данные векторы линейно зависимы.◄
Теорема 5. Три некомпланарных вектора  ,
,  и
и  линейно независимы.
линейно независимы.
► Предположим, что эти векторы линейно зависимы. Тогда какой-либо вектор этой системы можно представить в виде линейной комбинации других. Не нарушая общности, можно считать, что  , а это означает, что векторы
, а это означает, что векторы  ,
,  ,
,  , а, следовательно, и векторы
, а, следовательно, и векторы  ,
,  ,
,  принадлежат одной плоскости, т.е. компланарны.
принадлежат одной плоскости, т.е. компланарны.
Полученное противоречие доказывает теорему.◄
Из теорем 4 и 5 следует критерий компланарности трёх векторов.
Три вектора компланарны тогда и только тогда, когда хотя бы один из них может быть представлен в виде линейной комбинации других.
Теорема 6. Любой вектор  может быть разложен по трём некомпланарным векторам
может быть разложен по трём некомпланарным векторам  ,
,  и
и  , причем, единственным образом.
, причем, единственным образом.
 ►;Приложим начала всех векторов к точке
►;Приложим начала всех векторов к точке  (рис. 2.6). Из конца вектора
(рис. 2.6). Из конца вектора 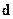 проведем прямую, параллельную вектору
проведем прямую, параллельную вектору  , до пересечения её с плоскостью векторов
, до пересечения её с плоскостью векторов  и
и  . Пусть
. Пусть  - точка пересечения этой прямой и плоскости. Очевидно,
- точка пересечения этой прямой и плоскости. Очевидно, 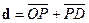 ,
,  ,
,
 и
и 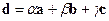 .
.
Рис. 2.6 Покажем единственность разложения
 (2.1)
(2.1)
Предположим противное, а именно, что существует ещё одно разложение (отличное от предыдущего)
 . (2.2)
. (2.2)
Пусть  . Вычитая (2.1) из (2.2), имеем
. Вычитая (2.1) из (2.2), имеем  . Так как
. Так как  , то вектор
, то вектор  может быть представлен в виде линейной векторов
может быть представлен в виде линейной векторов  и
и  , откуда следует, что векторы
, откуда следует, что векторы  ,
,  и
и  компланарны. Полученное противоречие доказывает теорему и, следовательно, разложение
компланарны. Полученное противоречие доказывает теорему и, следовательно, разложение  единственно.◄
единственно.◄
В пространстве геометрических векторов линейно независимыми являются:
1) один ненулевой вектор;
2) два неколлинеарных вектора;
3) три некомпланарных вектора.
Все остальные системы векторов являются линейно зависимыми.

 , где
, где  действительные числа, называется линейной комбинацией геометрических векторов
действительные числа, называется линейной комбинацией геометрических векторов  .
. и
и 
 линейно зависимы
линейно зависимы , то
, то  (знак плюс, если
(знак плюс, если  , и знак минус, если
, и знак минус, если  . Тогда
. Тогда , откуда следует, что
, откуда следует, что , но последнее означает, что векторы
, но последнее означает, что векторы  Теорема 3. Любой вектор плоскости можно разложить по двум неколлинеарным векторам, причем, единственным образом.
Теорема 3. Любой вектор плоскости можно разложить по двум неколлинеарным векторам, причем, единственным образом. (рис.2.5).
(рис.2.5). плоскости приложим к этому же началу. Из конца вектора
плоскости приложим к этому же началу. Из конца вектора  . Так как вектор
. Так как вектор 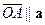 , то
, то , что
, что 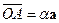 . Вектор
. Вектор  ,поэтому его можно представить в виде
,поэтому его можно представить в виде  . Тогда
. Тогда  .
. .
. . Не нарушая общности можно считать, что
. Не нарушая общности можно считать, что  . Вычитая последнее равенство из предыдущего, имеем
. Вычитая последнее равенство из предыдущего, имеем  , откуда следует, что
, откуда следует, что 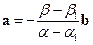 и векторы
и векторы  и векторы
и векторы  , а это означает, что векторы
, а это означает, что векторы  ,
,  , а, следовательно, и векторы
, а, следовательно, и векторы  может быть разложен по трём некомпланарным векторам
может быть разложен по трём некомпланарным векторам  ►;Приложим начала всех векторов к точке
►;Приложим начала всех векторов к точке 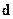 проведем прямую, параллельную вектору
проведем прямую, параллельную вектору  - точка пересечения этой прямой и плоскости. Очевидно,
- точка пересечения этой прямой и плоскости. Очевидно, 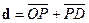 ,
,  ,
,  и
и 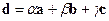 .
. (2.1)
(2.1) . (2.2)
. (2.2) . Так как
. Так как 


