Ранг и базис системы векторов.
Определение. Упорядоченная, линейно независимая подсистема данной системы векторов, содержащая наибольшее количество векторов, называется базисом данной системы векторов. Иначе говоря, векторы а) векторы б) векторы Векторы, входящие в базис, называются базисными. Из определения базиса следует, что все базисы системы векторов содержат одинаковое количество базисных векторов. Определение. Рангом Пишут Так как в пространстве геометрических векторов все системы, содержащие более трёх векторов, линейно зависимы, то базис в этом пространстве содержит не более трёх векторов и ранг такой системы не более трёх. ●; Решение. Векторы Рис. 2.7 Векторы Векторы Возможные базисы:
|

 образуют базис системы векторов
образуют базис системы векторов 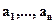 , если выполняются два условия:
, если выполняются два условия: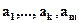 – линейно зависимы для любого вектора
– линейно зависимы для любого вектора  данной системы, не входящего в базис.
данной системы, не входящего в базис. системы векторов называется число, равное числу векторов, входящих в базис.
системы векторов называется число, равное числу векторов, входящих в базис. -базис,
-базис, 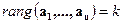 .
. Пример 1. Дан параллелепипед.Найти базис и ранг системы векторов
Пример 1. Дан параллелепипед.Найти базис и ранг системы векторов  ,
,  ,
,  и
и 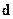 (рис.2.7).
(рис.2.7).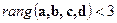 .
. ,
,  ,
,  ,
,  ,
,  и
и  ,
,  ,
,  ,
,  ,
,  .
.



