Организационный момент
Притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.
1. С каким математическим понятием связаны слова:
Основание
Показатель (Степень)
Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Действительное число)
Сформулируйте тему урока. (Степень с действительным показателем)
2. Какая наша стратегическая цель? (ЕГЭ)
Какие цели нашего урока?
– Обобщить понятие степени.
Задачи:
– повторить свойства степени
– рассмотреть применение свойств степени при вычислениях и упрощениях выражений
– отработка вычислительных навыков.
3. Итак, ар, где р – число действительное.
Приведите примеры (выберете из выражений 5–2,  , 43,
, 43,  ) степени
) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем
4. При каких значениях а имеет смысл выражение
аn, где n  (а – любое)
(а – любое)
аm, где m  (а
(а  0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
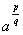 , где
, где  (а
(а  0)
0)
5. Из данных выражений выберете те, которые смысла не имеют:
(–3)2,  ,
,  , 0–3,
, 0–3,  , (–3)–1,
, (–3)–1,  .
.
6. Вычислите. Ответы в каждом столбике обладают одним общим свойством. Укажите лишний ответ (этим свойством не обладающий)
 = 2
= 2 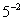 =
= 
 =
= 
 = 6
= 6  =
=  (неправ. др.)
(неправ. др.)  =
=  (нельзя записать дес. др.)
(нельзя записать дес. др.)
 =
=  (дробь)
(дробь)  =
= 
 =
= 
7. Какие действия (математические операции) можно выполнять со степенями?
Установите соответствие:
| При умножении степеней с равными основаниями
| Основания умножаются, а показатель остаётся прежним
|
| При делении степеней с равными основаниями
| Основания делятся, а показатель остаётся прежним
|
| При возведении степени в степень
| Основание остаётся прежним, а показатели умножаются
|
| При умножении степеней с равными показателями
| Основание остаётся прежним, а показатели вычитаются
|
| При делении степеней с равными показателями
| Основание остаётся прежним, а показатели складываются
|
Один ученик записывает формулы (свойства) в общем виде.
8. Дополнить степени из п.3 так, чтобы к полученному примеру можно было применить свойства степени.
(Один человек работает у доски, остальные в тетрадях. Для проверки обменяться тетрадями, а ещё один выполняет действия на доске)
9. На доске (работает ученик):
Вычислите  :
:  =
=
Самостоятельно (с проверкой на листах)
 =
=
 =
=
Какой из ответов не может получиться в части «В» на ЕГЭ? Если в ответе получилось  , то как записать такой ответ в части «В»?
, то как записать такой ответ в части «В»?
10. Самостоятельное выполнение задания (с проверкой у доски – несколько человек)
Задание с выбором ответа
|
|
|
|
|
|
|
|
| 
| 
| 25 –  
|
| 
|
|
|  : : 
| 
| 
| –7 
| –9
|
|
| 0,3 
| 9,1
| 2,9
| 89,9
| 8,9
|
|
| 
|
|
| 2,5
|
|
11. Задание с кратким ответом (решение у доски):
 +
+  + (60)5
+ (60)5 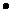 2 – 3–4
2 – 3–4 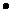

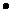 27 =
27 =
Самостоятельно с проверкой на скрытой доске:
 –
–  – 32
– 32 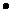 2– 4
2– 4 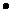
 + (30)4
+ (30)4 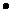 4 =
4 =
12. Сократите дробь (на доске):
 =
=
В это время один человек решает на доске самостоятельно:  = (класс проверяет)
= (класс проверяет)
13. Самостоятельное решение (на проверку)
На отметку «3»: Тест с выбором ответа:
1. Укажите выражение, равное степени 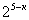
2. Представьте в виде степени произведение:

3. Упростите выражение

:

и найдите его значение при х = 2
1. 
| 2. 8
| 3. 
| 4. – 8
|
4. Чему равно значение выражения
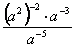
при а =

| 1. – 9
| 2. 
| 3. 
| 4. 9
|
5. Вычислите

1. 
| 2. 
| 3. 16
| 4. – 16
|
На отметку «4»: № 439 (1, 2, 4, 5, 6)
На отметку «5»:
1. 
2. Упростите выражение 
14. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями:
Сравните числа  и
и 
15. Дома:№438,придумать по 2 примера на свойства степени.
В заключение урока:
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей»
– Так сказал американский математик Морис Клайн.
– Спасибо за урок!

 :
:  и найдите его значение при х = 2
и найдите его значение при х = 2
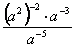 при а =
при а = 


 , 43,
, 43,  ) степени
) степени (а – любое)
(а – любое) (а
(а  0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?
0) Как от степени с отрицательным показателем перейти к степени с положительным показателем?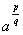 , где
, где  (а
(а  0)
0) ,
,  , 0–3,
, 0–3,  , (–3)–1,
, (–3)–1,  .
. = 2
= 2 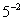 =
= 
 =
= 
 = 6
= 6  =
=  (неправ. др.)
(неправ. др.)  =
=  (нельзя записать дес. др.)
(нельзя записать дес. др.) =
=  (дробь)
(дробь)  =
= 
 =
= 
 :
:  =
= =
=  =
= , то как записать такой ответ в части «В»?
, то как записать такой ответ в части «В»?




 :
: 





 +
+  + (60)5
+ (60)5 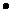 2 – 3–4
2 – 3–4 
 –
–  – 32
– 32  + (30)4
+ (30)4  =
= = (класс проверяет)
= (класс проверяет)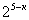















 и
и 



