В. Усложненные функции затрат
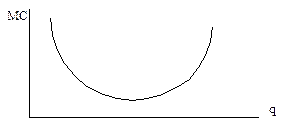
Очень часто приходится сталкиваться с усложненными функциями затрат, основанными на законе убывающей производительности (тема 6, п. 2). Его действие ведет к тому, что предельные затраты после первоначального снижения, рано или поздно начинают расти (рис. 7-5): Рис. 7-5. Кривая предельных затрат
Это означает, что первоначально каждая следующая единица выпуска требует все меньших дополнительных затрат, а затем тенденция сменяется на противоположную: чем больше выпуск, тем дороже обходится каждая следующая его единица. Такая динамика предельных, соответственно и средних переменных затрат обусловлена динамикой предельного и среднего продукта переменного фактора производства – труда, рассмотренной в теме 6, п. 2. Напомним, что предельный и средний продукты сначала увеличиваются, потом достигают максимума, а затем начинают убывать. Так вот, пока предельный (средний) продукт труда возрастает, предельные (средние переменные) затраты снижаются; в тот момент, когда предельный (средний) продукт труда достигает максимума, предельные (средние переменные) затраты становятся минимальны; если предельный (средний) продукт труда начинает падать, предельные (средние переменные) затраты возрастают. Приведем условный числовой пример. При этом нам изначально известны величина постоянных затрат, а также динамика переменных затрат в зависимости от изменения выпуска. Все прочие затраты являются расчетными (табл. 7-2): Табл. 7-2. Усложненный вариант динамики затрат
В таком случае функции переменных и совокупных затрат перестают быть линейными, хотя линии TC и VC по-прежнему параллельны друг другу, и кривая ТС выходит из точки постоянных затрат (рис. 7-6А): Рис. 7-6. Функции переменных, совокупных, предельных, средних переменных и средних совокупных затрат
Характер кривых переменных и совокупных затрат обусловлен динамикой предельных затрат. До тех пор, пока предельные затраты убывают, переменные и совокупные затраты возрастают медленнее, нежели выпуск. На рис. 7-6А это отражено выпуклостью кривых VC и TC вверх вплоть до точек перегиба (т. А и А’). При выпуске, соответствующем точкам перегиба (q’), предельные затраты достигают минимума. Затем они начинают возрастать, в результате чего переменные и совокупные затраты увеличиваются быстрее, чем выпуск. Это означает, что кривые VC и TC становятся выпуклыми вниз. Функция предельных затрат определяет и вид кривых средних переменных и средних совокупных затрат (рис. 7-6Б). Кривые MC и AVC выходят из одной точки: для бесконечно малых величин они равны. Затем предельные затраты снижаются и «тянут за собой» средние переменные затраты, которые тоже падают, но медленнее. При определенном уровне выпуска (q’) предельные затраты достигают своего минимума. Далее предельные затраты начинают повышаться, увлекая за собой средние переменные затраты, хотя последние еще некоторое время «по инерции» падают. Дело в том, что средние переменные затраты снижаются до тех пор, пока они больше предельных затрат. Кривая предельных затрат сечет, следовательно, кривую AVC и в точке ее минимума, после чего обе функции возрастают. Кривая средних совокупных затрат (AC) выходит из бесконечности, поскольку при производстве, близком к нулю, постоянные затраты все равно приходится нести, и, следовательно, совокупные затраты на единицу выпуска очень высоки. Затем средние совокупные затраты падают, достигая минимума в точке пересечения с кривой предельных затрат. Точка минимума средних совокупных затрат находится правее точки минимума средних переменных затрат. Это объясняется тем, что средние совокупные затраты включают в себя не только средние переменные, но и средние постоянные затраты, а последние все время снижаются. По мере повышения выпуска кривые AC и AVC постоянно сближаются, поскольку средние постоянные затраты стремятся к нулю.
|