Решение. перераспределение зарядов в стержне происходит под действием магнитной составляющей силы Лоренцаперераспределение зарядов в стержне происходит под действием магнитной составляющей силы Лоренца
являющейся в данном случае сторонней. Если стержень вращается так, как показано на рис. 18.20 (ось вращения проходит через точку О), то электроны будут накапливаться на закрепленном конце стержня. Заряды разных знаков накапливаются на концах стержня до тех пор, пока электрическая сила созданного ими кулоновского поля не уравновесит магнитную силу Лоренца:
или
Вращающийся стержень пронизывается переменным магнитным потоком, и, в соответствии с законом электромагнитной индукции, в нем наводится (индуцируется) ЭДС индукции, и между двумя любыми точками стержня возникает разность потенциалов
Подставив в формулу (18.33) величину
Для проведения расчета введем радиус-вектор Учитывая коллинеарность векторов
При интегрировании от т. О до т. С r изменяется от 0 до
Подставим численные значения и выполним вычисления:
|
, (18.30)
,(18.31)
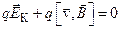. (18.32)
. (18.33)
из уравнения (18.32) получим
. (18.34)
, направленный от оси вращения вдоль стержня. Вектор линейной скорости 
любой точки стержня перпендикулярен вектору 
. Вектор 
направлен по стержню от оси вращения. Это направление сохранится в любом положении стержня. Таким образом, вектор 
.
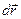и выражая линейную скорость, различную для разных точек стержня, через угловую (v = w r), получаем:
. (18.35)
. Таким образом, подставляя (18.34) в (18.33) и учитывая пределы интегрирования, получаем:
.(18.36)
.
