Составил В.Г. Каналин 1 страница. Неправильное создание семьи – причина войн и гибели цивилизаций.
Неправильное создание семьи – причина войн и гибели цивилизаций. Чего хотят женщины, открыты законы социального происхождения человека. История двух видов: человека Происхождение человека разумного знания объединены в тексте в единое мировоззрение. Как преуспеть в любви – найти и жену и Снегурочку! Объединяющая власть женщины королевского возраста. Открыты законы происхождения человека разумного. Предупреждение о смертельной угрозе, нависшей над человечеством! Назовите имя. происхождения семьи. правление – причина войн и гибели цивилизаций. Правитель разожжёт войну и спрячется в бункер! Спаси свою Снегурочку, и ты спасёшь цивилизацию! Предупреждение о смертельной Происхождение человека разумного и Снегурочек. Открыты законы естественной репродукции: кроме жены нужна ещё и Снегурочка! что письмо дошло! Объединяющая власть женщины королевского возраста. Bitte übermitteln Sie Angela Merkel! Stellen aufsteigen Heimat - Mutter Deutschen Landen! Как преуспеть в любви – найти и жену и Снегурочку! Правитель разожжёт войну и спрячется в бункер! Спаси свою Снегурочку, и ты спасёшь цивилизацию! Предупреждение о смертельной угрозе,нависшей над человечеством! Происхождение человека разумного и Снегурочек, открыты законы естественной репродукции человека разумного. Как создать семью, открыты законы естественной репродукции человека разумного. ? Семья, любовь, секс. Открыты законы естественной репродукции человека разумного. Про любовь, Снегурочек и Дедов Морозов, открыты законы естественной репродукции человека разумного. Любовь семья секс открыты законы происхождения Объединяющая власть женщины королевского возраста. Открыты законы происхождения человека разумного. Предупреждение о смертельной угрозе, нависшей над человечеством! Назовите имя.
происхождения семьи. правление – причина войн и гибели цивилизаций. Правитель разожжёт войну и спрячется в бункер!
Offene Gesetze Ursprung des Homo sapiens! Open laws origin of Homo sapiens! Program evolution united humanity. Открыты законы происхождения человека разумного, найдена причина гибели цивилизаций. Не делайте революцию, нужна эволюция! Программа эволюции объединённого человечества. Статьи в прикреплённом файле.
Ursprung des Homo sapiens! Open laws origin of Homo sapiens!
Почему не удалось создать семью
Открыты высшие законы человеческого общества.
Открыты законы репродукции: не все, кто с паспортом, являются людьми. Открыты законы происхождения человека разумного, чтобы объединить разумных людей в оппозиции, нужно единое мировоззрение.
Чтобы объединить разумных людей в оппозиции, нужно единое мировоззрение. Открыты законы происхождения человека разумного 75.ppgp@civilplatform.ru
СМИ не говорят правду людям и благополучно дождутся гибели цивилизации
Запрещённые знания о создании семьи и рождении детей.
. Stellen aufsteigen Heimat - Mutter Deutschen Landen!
Wrong way to create the family is a reason for wars and civilizations destruction
Открыты законы репродукции: не все, кто с паспортом, являются людьми. Составил В.Г. Каналин 1-71 – см. рис.41
Стабильность и выдержанность выделенных групп эксплуатационных объектов сравнивались с результатами группирования по другим вариантам набора геолого-промысловых признаков. По некоторым вариантам обособлялось, например, положение V группы или отдельных многопластовых эксплуатационных объектов (Мухановское месторождение, объект Д-I+ДII+Д-III+Д-IV). Поэтому в качестве оптимального можно принять вариант IV, где выделенные группы и подгруппы имеют довольно определенные границы. Все вышеизложенное позволяет говорить о возможности группирования эксплуатационных объектов по комплексу геолого-промысловых признаков. Естественно, что эти исследования надо продолжить с тем, чтобы иметь необходимую информацию по всем нефтедобывающим районам страны. При группировании нефтяных залежей учитываются те же геолого-промысловые признаки, что и при оценке коэффициента продуктивности по косвенным признакам. Эти материалы могут быть использованы при оценке степени различия (сходства) пластов при разработке метода обоснования целесообразности объединения залежей продуктивных пластов в один эксплуатационный объект на том или другом многопластовом месторождении.
Глава 19. ОЦЕНКА ВЛИЯНИЯ СТЕПЕНИ РАЗЛИЧИЯ МЕЖДУ ПЛАСТАМИ НА РЕЗУЛЬТАТЫ ИХ СОВМЕСТНОЙ ЭКСПЛУАТАЦИИ 19.1 Возможность оценки коэффициента продуктивности по косвенным данным Для определения Имеются лишь ограниченные сведения о возможности оценки коэффициента продуктивности по косвенным данным. Так, в работе В.Г. Ингермана говорится о возможности оценки удельного коэффициента продуктивности с помощью проницаемости, рассчитанной по промыслово-геофизическим данным, в работе [1] — о возможности определения коэффициента продуктивности по комплексу геологических параметров, а в другой работе —с учетом некоторых геофизических признаков (ρпαсп). Исследования, проведенные нами на разрабатываемых нефтяных месторождениях Западной Сибири (Усть-Балыкском, Западно-Сургутском, Правдинском, Самотлорском, Советском), показали, что К могут быть определены с помощью многомерного регрессионного анализа, реализованного в виде соответствующих программ. Для выполнения необходимых расчетов была составлена соответствующая программа. В общем случае задачей регрессионного анализа является оценка условного математического ожидания (М)случайной величины I при заданном значении другой переменной. Сущность метода многомерного регрессионного анализа заключается в вычислении оценки математического ожидания коэффициента продуктивности по фиксированным значениям геолого-физических признаков, которые характеризуют изучаемый пласт в каждом его пересечении скважиной. Как известно, получаемый при этом коэффициент множественной корреляции R оценивает тесноту связи между определяемым параметром (зависимой переменной) и параметрами, по которым ведется оценка (независимые переменные). Через множественный коэффициент корреляции вычисляется и среднеквадратическая погрешность (σ) оценки зависимой переменной при фиксированных значениях независимых переменных
где Оценка коэффициента множественной корреляции по эмпирическим данным является случайной величиной, которая определяется составом выборки и количеством наблюдений (N) в выборке, В силу случайности выборки можно получить ненулевые значения R, в то время как истинное значение его (вычисленное для генеральной совокупности) равно нулю. Для проверки гипотезы, которая состоит в предположении, что R=0, используется критерий Фишера [2]. Считается, что эмпирические данные не противоречат гипотезе, если
где R – коэффициент множественной корреляции; N – количество наблюдений; р – количество переменных, вошедших в уравнение; F(р–1; N–р; α) – критическая точка распределения Фишера для р – 1 и N – р степеней свободы и выбранного уровня значимости α (обычно α=0,05) Если неравенство (19.2) не выполняется, то принимается, что R≠0 и говорят, что значение R статистически значимо. Например, коэффициент корреляции, полученный для пласта БС6 Правдинского месторождения (R=0,5 N=51),является статистически незначимым. Действительно,
что меньше значения F (7;43; 0,05) = 2,20. Кроме того, для расчетов выбирается такое уравнение, для которого погрешность получаемого результата является минимальной. В математическом отношении решаемая задача является обратной и принадлежит к числу так называемых некорректных задач, поскольку используемые в ней параметры могут быть, с одной стороны, определены с некоторой степенью приближения, а с другой, связаны с коэффициентом продуктивности только косвенно. Поэтому успешность реализации поставленной задачи будет во многом зависеть от набора необходимых признаков. При оценке коэффициента продуктивности по косвенным данным необходимо подобрать такие признаки, от которых этот параметр будет наиболее зависеть. Как известно [18], продуктивность скважины тесно связана с гидропроводностью. Следовательно, необходимо выбрать такие геолого-промысловые и геофизические признаки, которые бы характеризовали именно этот сложный фильтрационный параметр. Поэтому для определения Kiнужно выделить геолого-физические признаки, характеризующие условия движения нефти по пласту. Это эффективная мощность, проницаемость, вязкость нефти, песчанистость и расчлененность. Эти признаки можно отнести к первой группе. Поскольку геофизическими методами исследуются все пробуренные скважины, можно проследить связь между результатами таких исследований и коэффициентом продуктивности Кi. Впервые влияние фильтрационных свойств пласта на его удельное сопротивление было показано Г.С. Морозовым. Другие исследователи считают, что при регрессионной оценке коллекторских свойств лучшие результаты дает использование кажущихся удельных сопротивлений (ρк) [41]. В работе [9] четко показана зависимость относительной амплитуды на диаграммах СП(αсп) от проницаемости, т. е. αсп=f(kпр). В общем случае αсп характеризует глинистость пласта и его фильтрационные особенности. Кроме того, можно отметить наличие статистических связей: αсп=f(kпр); αсп/αим= f(kпр); Рн=f(kпр) и т.д. [24]. Например, для пластов АВ1-5 Самотлорского и Советского месторождений установлена тесная связь проницаемости с αсп, определяющаяся соотношением [24] αсп=0,22lg kпр+0,14. (19.3) В этой же работе [24] приводится характеристика статистических связей между kпр и физическими параметрами (табл. 31). Таблица 31 Характеристика статистических связей коэффициента проницаемости с геофизическими параметрами Рн, αсп и αим продуктивных пластов Самотлорского месторождения (по данным Е.И. Леонтьева)
Примечание. Относительные ошибки Е=∆Х/Ymax – Ymin даны с вероятностью 0,95.
Для практических расчетов Kпр по отдельным пластам месторождений Западной Сибири использовались зависимости, которые приведены в табл.32. При сравнении результатов расчетов проницаемости, определенной гидродинамическими и геофизическими методами, выясняется большая разница значений, что свидетельствует о малой информативности отмеченных выше признаков для оценки проницаемости, а следовательно, и для вычисления коэффициентов продуктивности. Как указывается, В.Г. Ингерманом, при решении данной задачи кроме αсп должны учитываться либо удельное электрическое сопротивление (ρп), либо кажущееся удельное сопротивление ρк. Во вторую группу признаков нами были включены кажущиеся сопротивления, зарегистрированные зондами длиной 0,45; 1,0; 2,25; 4,25 м (ρ0,45; ρ1,05; ρ2,25; ρ4,25) и относительная амплитуда собственного потенциала скважин αсп. Таблица 32 Зависимость коэффициента проницаемости от геофизических параметров (по данным СибНИИНП)
При снятии значений кажущихся удельных сопротивлений с диаграмм электрометрии мы брали их средние значения в интервале пласта. Ряд исследователей предлагают снимать значения ρкi через каждые 0,8 м и среднее значение признака определять как Поиск необходимых уравнений регрессии проводился в два этапа. На первом учитывались только геолого-физические признаки, на втором в пространство геолого-физических признаков вводились данные промысловой геофизики. Всего было проанализировано около 450 различных выборок, характеризующихся различными наборами признаков, по продуктивным пластам Усть-Балыкского, Западно-Сургутского, Правдинского, Самотлорского, Советского, Ватинского месторождений, находящихся в разработке. В результате исследований на первом этапе было установлено, что коэффициент продуктивности весьма тесно связан не только с такими геолого-физическими параметрами, как эффективная мощность, проницаемость (по керну и по КВД), вязкость нефти в пластовых условиях, но и с такими, как коэффициенты песчанистости и расчлененности. Множественные коэффициенты корреляции для разных пластов отмеченных выше месторождений меняются от 0,7 до 0,975 (табл. 33), т.е. коэффициенты корреляции весьма высокие. Таблица 33 Статистические связи коэффициента продуктивности с геолого-промысловыми признаками
Ввиду того, что проницаемость по смежным пластам по разведочным и особенно по эксплуатационным скважинам как по лабораторным анализам керна, так и по гидродинамическим методам не определяется, во второй группе экспериментов на этом этапе вместо проницаемости, вычисленной гидродинамическими методами, включалось значение проницаемости, рассчитанной методами промысловой геофизики по уравнениям табл. 31, 32. Полученные уравнения регрессии (табл. 34) невозможно использовать (кроме пласта БС1 Западно-Сургутского месторождения) для практических расчетов коэффициента продуктивности. На втором этапе исследований в уравнения табл.33 вместо проницаемости вводились те геофизические признаки, которые тесно связаны с фильтрационными свойствами пород. Включение геофизических параметров в признаковое пространство несколько понизило значения множественных коэффициентов корреляции R. В ряде случаев связь оказывается хуже, значения R колеблются от 0,3 до 0,95. Таблица 34 Статистические связи коэффициента продуктивности с геолого-промысловыми признаками и проницаемостью, рассчитанной по материалам промысловой геофизики
На следующем этапе работ при вычислении коэффициента продуктивности Кi оценивалась информативность различных геофизических признаков. Для этой цели нами кроме самих геолого-физических признаков использованы и некоторые комплексные параметры, связанные с Кi: 1) Согласно расчетным данным комплексные параметры для оценки коэффициента продуктивности являются более информативными, чем геофизические характеристики. Поэтому в дальнейшем мы пользовались следующим набором признаков: Нэ; kp; kпч; Установив информативность геолого-геофизических признаков, следует остановиться на оценке получаемых типов регрессий (линейной или нелинейной). Уравнения линейной регрессии для оценки коэффициента продуктивности по отмеченным признакам характеризуются низкими значениями множественного коэффициента корреляции. Так, например, для пласта БС1 Усть-Балыкского месторождения по 53 скважинам было получено линейное уравнение, которому соответствует множественный коэффициент корреляции, равный 0,58; для пласта БС6 Правдинского месторождения — равный 0,5. Следовательно, такая оценка коэффициента продуктивности регрессии приводит к низким коэффициентам множественной корреляции, вплоть до статистически незначимых. В связи с этим возникает необходимость использовать нелинейные уравнения. Здесь возникает проблема методологического характера, а именно — в настоящее время нет ни теоретического, ни практического обоснования того, какой вид должно иметь нелинейное уравнение регрессии, т.е. каким нелинейным преобразованиям должны подвергаться исходные геолого-геофизические признаки для того, чтобы можно было получать высокие коэффициенты множественной корреляции. Так обстоит дело не только при оценке коэффициента продуктивности, но и при оценке многих других геологических, геолого-промысловых и геофизических характеристик. На практике обычно поступают следующим образом [41]. Наряду с исходным набором признаков (Х1, Х2,…, Хр), рассматриваются функции φ1(xi), φ2(xi),…, φm(xi), i=1, 2,…, рот всех или некоторых признаков. Обычно это наиболее простые непрерывные функции: ln(xi), (xi)2, Затем рассматриваются различные комбинации некоторых признаков новой системы и строятся линейные уравнения регрессии относительно этих преобразованных к нелинейному виду признаков, т.е.
Это обычно или многочлен второй степени, или линейная форма заранее задаваемого вида. С целью выбора вида линейной формы в отмеченных работах производится расчет различных статистических характеристик исходных и преобразованных данных. При построении нелинейных уравнений-регрессий по геолого-геофизическим признакам (19.4) строились линейные формы по этим признакам по (19.6), а также по их нелинейным преобразованиям (19. 5). При этом вид уравнения заранее не задавался, оно строилось с помощью пошаговой процедуры, использующей для отбора признаков частные коэффициенты корреляции. На первом шаге процедуры выбирается такой признак (или его функция), который лучше других признаков объясняет дисперсию оцениваемого параметра (в нашем случае коэффициента продуктивности K). Другими словами, отбирается признак, имеющий наибольший парный с К коэффициент корреляции, и вычисляется доля дисперсии, которая не объясняется выбранным признаком (остаточная дисперсия). На втором шаге процедуры в уравнение регрессии включается признак (или его функция), объясняющий остаточную дисперсию лучше, чем другие признаки, т.е. выбирается признак, который имеет наибольший частный коэффициент корреляции с K при исключении влияния первого выбранного признака. Далее отбор признаков ведется по следующему индуктивному правилу. Пусть уже отобрано tпризнаков. На t+1 шаге выбирается такой признак (или его функция), который имеет максимальный частный коэффициент корреляции с оцениваемым признаком, при исключении влияния первых tпризнаков. Другими словами, на t+1 шаге выбирается такой признак, который наилучшим образом объясняет ту долю дисперсии оцениваемого признака, которую не могут объяснить первые выбранные tпризнаки. Такой отбор признаков обеспечивает рост множественного коэффициента корреляции на каждом шаге процедуры. Как показывает опыт расчетов, при оценке коэффициента продуктивности по геолого-промысловым и геофизическим признакам по (19.4) е использованием нелинейностей (19.5) значения R испытывают значительный рост на первых пяти-шести шагах процедуры и после восьми-девяти шагов уже практически не изменяются. Например, при построении уравнения для пласта БС1 Усть-Балыкского месторождения значения Rот шага к шагу менялись следующим образом: R=0,34; R=0,49; R=0,57; R=0,65; R=0,69; R =0,73; R=0,78; R=0,8; R=0,82. Отсюда видно, что уравнение, содержащее пять признаков (табл.35, уравнение 1), может использоваться для расчетов, так как добавление еще четырех признаков (уравнение 2) лишь на 0,05 изменяет коэффициент множественной корреляции, а громоздко намного более, чем уравнение 1. R5, R9 являются статистически значимыми согласно (19.2), поэтому для более точных расчетов следует использовать уравнение 2.
|
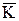совмобъекта необходимо знать значения Kсовм для каждой разведочной или эксплуатационной скважины, эксплуатирующей совместно несколько продуктивных пластов. Для этого, в свою очередь в тех же скважинах должны быть известны значения Кiпри условии самостоятельной эксплуатации каждого из совместно разрабатываемых пластов. Однако применяемые в настоящее время технология промысловых исследований скважин, эксплуатирующих несколько пластов, обычно позволяет определить лишь Kсовм. Значения Кiкаждого из пластов при условии их самостоятельной эксплуатации обычно не определяются. Следовательно, необходимо найти способ определения Ki для скважин, по которым известны Kсовм. Причем для месторождений, вводимых в разработку, необходимо устанавливать такие зависимости для одного или нескольких пластов, относящихся к одной группе.
, (19.1)
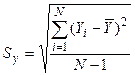—оценка среднего квадратического отклонения зависимой переменной (Y). Из этого выражения следует, что чем ближе значение R к единице, тем меньше разброс эмпирических точек относительно плоскости регрессии.
, (19.2)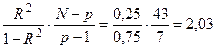
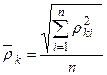. В этом случае, естественно, повышается объективность определения значений кажущихся сопротивлений, однако полученная величина 
, во-первых, не имеет физического смысла, а во-вторых, лишь на 15 - 17% отличается от средних значений, снимаемых непосредственно с диаграмм. Кроме того, объем вычислительных работ возрастает в несколько раз.
; 2) 
; 3) 
, 4) 
.
; 
; 
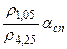, (xi)3, ln2(xi), xixy и др. (19.5)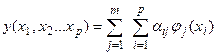
. (19.6)
