Условия равновесия на границе двух сред (жидкость - тв. тело). Смачивание.
Рассмотрим условия смачивания и несмачивания на границе жидкости с твердым телом. Следует отметить, что поверхностным натяжением обладают не только жидкости, но и твердые тела. Наличие в твердых телах строго периодической кристаллической структуры свидетельствует о наличии в них сил притяжения между молекулами. Благодаря наличию этих сил поверхностное натяжение возникает и в твердых телах. Рис1 Пусть капля жидкости 2 помещена на поверхность твердого тела 1 (рис.1). На рисунке указаны силы поверхностного натяжения, действующие на границе жидкость-твердое тело ( Рассмотрим два случая. Если Угол θ при этом является острым (рис.2). Некоторые жидкости на поверхности твердого тела образуют капли, равновесная форма которых определяется неравенством
45.Давление под искривлённой поверхностью. Капилляры и капиллярные явления. Формула Лапласа. При своем стремлении к сокращению поверхностная пленка создает добавочное давление. Давление, которое всегда существует внутри жидкости, увеличивается, когда ее поверхность выпуклая, и уменьшается под вогнутой поверхностью.Влияние кривизны поверхности на давление внутри жидкости.В существовании этого влияния можно убедиться на простом опыте. Возьмем стеклянную воронку с изогнутой под прямым углом трубкой. Направим конец воронки с выдутым мыльным пузырем на пламя свечи Мы заметим что пламя свечи отклоняется. Это говорит о том что из воронки воздух вытекает, значит, давление воздуха в пузыре больше атмосферного.Проведем еще один опыт. Соединим широкий сосуд А при помощи резиновой трубки с узкой стеклянной трубкой. Наполним эти сообщающиеся сосуды водой. Сначала установим конец трубки В на уровне жидкости в сосуде А В этом случае поверхность воды в трубке В, как и сосуде А, является плоской (рис. а). Так как вода в обоих сосудах находится на одном горизонтальном уровне, то давление непосредственно под плоской поверхностью жидкости в обоих сосудах одинаково и равно атмосферному.Станем медленно опускать трубку В. Мы заметим, что поверхность воды в ней приобрела выпуклую сферическую форму (рис. б). Теперь вода в сосуде А и трубке В находится не на одном уровне. Если продолжать опускать трубку В, то поверхность воды будет выгибаться все больше и больше (радиус сферической поверхности воды уменьшатся) пока не примет форму полусферы. Так как жидкость в сообщающихся сосудах А и В находится в равновесии, то у конца В непосредственно под выпуклой поверхностью давление будет больше атмосферного на величину равную Если размеры сосуда, в котором наход жидкость, илди, если расстоян между поверхн, огранич жидкость,сравнимы с радиусом кривизны роверхн жидкостьи, то такие сосуды назыв капиллярными.явления происход в таких слсудах наз капиллярными. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ, поверхностные явления на границе жидкости с др. средой, связанные с искривлением ее пов-сти. Искривление пов-сти жидкости на границе с газовой фазой происходит в результате действия поверхностного натяжения жидкости, к-рое стремится сократить пов-сть раздела и придать ограниченному объему жидкости форму шара. Поскольку шар обладает миним. пов-стью при данном объеме, такая форма отвечает минимуму поверхностной энергии жидкости, т.е. ее устойчивому равновесному состоянию. Капиляры ярко выражены и играют существ. роль в условиях невесомости, при дроблении жидкости в газовой среде (или распылении газа в жидкости) и образовании систем, состоящих из мн. капель или пузырьков (эмульсий, аэрозолей, пен), при зарождении новой фазы капель жидкости при конденсации паров, пузырьков пара при вскипании, зародышей кристаллизации. Капиллярное давление. Т. к. силы поверхностного натяжения направлены по касательной к пов-сти жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина к-рого Dp связана со средним радиусом кривизны пов-сти r0 ур-нием Лапласа: Dp = p1 - p2 = 2s12/r0, (1) где p1 и p2 - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s12 - поверхностное (межфазное) натяжение. Если пов-сть жидкости вогнута (r0<0), давление в ней оказывается пониженным по сравнению с давлением в соседней фазе p1 < р2 и Dp < 0. Для выпуклых пов-стей (r0 > 0) знак Dp изменяется на обратный. Отрицат. капиллярное давление, возникающее в случае смачивания жидкостью стенок капилляра, приводит к тому, что жидкость будет всасываться в капилляр до тех пор, пока вес столба жидкости высотой h не уравновесит перепад давления Dp. В состоянии равновесия высота капиллярного поднятия определяется ф-лой Жюрена: где r1 и r2 - плотности жидкости 1 и среды 2, g - ускорение силы тяжести, r - радиус капилляра, q - краевой угол смачиванияКапиллярная пропитка. Понижение давления под вогнутыми менисками - одна из причин капиллярного перемещения жидкости в сторону менисков с меньшим радиусом кривизны. Частным случаем этого является пропитка пористых тел - самопроизвольное всасывание жидкостей в лиофильные поры и капилляры Скорость v перемещения мениска в горизонтально расположенном капилляре (или в очень тонком вертикальном капилляре, когда влияние силы тяжести мало) определяется ур-нием Пуазёйля:
|

 ), жидкость-газ (
), жидкость-газ ( ) и твердое тело-газ (
) и твердое тело-газ ( ). Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.
). Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.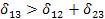 ,то жидкость 2 растекается по поверхности тела 1 до образования очень тонкой пленки вплоть до образования мономолекулярного слоя. При выполнении этого условия наступает полное смачивание жидкостью поверхности твердого тела. Угол θ при этом равен 0. Если при некотором соотношении между
,то жидкость 2 растекается по поверхности тела 1 до образования очень тонкой пленки вплоть до образования мономолекулярного слоя. При выполнении этого условия наступает полное смачивание жидкостью поверхности твердого тела. Угол θ при этом равен 0. Если при некотором соотношении между  , а также значении косинус оказывается справедливым равенство:
, а также значении косинус оказывается справедливым равенство:  ;то имеет место так называемое неполное смачивание. Жидкость 2 растекается по поверхности твердого тела до тех пор, пока не выполнится равенство
;то имеет место так называемое неполное смачивание. Жидкость 2 растекается по поверхности твердого тела до тех пор, пока не выполнится равенство  о имеет место так называемое неполное смачивание. При этом угол θ является тупым углом (рис.3). Силы
о имеет место так называемое неполное смачивание. При этом угол θ является тупым углом (рис.3). Силы 
 тремятся придать капле сферическую форму, чему препятствует действующая на каплю сила тяжести. В этом случае имеет место частичное несмачивание. В реальной ситуации при взаимодействии жидкости с твердым телом реализуются, как правило, две возможности – либо частичное смачивание(
тремятся придать капле сферическую форму, чему препятствует действующая на каплю сила тяжести. В этом случае имеет место частичное несмачивание. В реальной ситуации при взаимодействии жидкости с твердым телом реализуются, как правило, две возможности – либо частичное смачивание( , либо частичное несмачивание(
, либо частичное несмачивание( . Смачивание, явление, возникающее при соприкосновении жидкости с поверхностью твёрдого тела или другие жидкости. Оно выражается, в частности, в растекании жидкости по твёрдой поверхности, находящейся в контакте с газом (паром) или другой жидкостью, пропитывании пористых тел и порошков, искривлении поверхности жидкости у поверхности твёрдого тела. Так, Смачивание вызывает образование сферического мениска в капиллярной трубке, определяет форму капли на твёрдой поверхности или форму газового пузырька, прилипшего к поверхности погруженного в жидкость тела. Смачивание часто рассматривают как результат межмолекулярного (вандерваальсова) взаимодействия в зоне контакта трёх фаз (тел, сред). Однако во многих случаях, например при соприкосновении жидких металлов с твёрдыми металлами, окислами, алмазом, графитом, Смачивание обусловлено не столько межмолекулярным взаимодействием, сколько образованием химических соединений, твёрдых и жидких растворов, диффузионными процессами в поверхностном слое смачиваемого тела.
. Смачивание, явление, возникающее при соприкосновении жидкости с поверхностью твёрдого тела или другие жидкости. Оно выражается, в частности, в растекании жидкости по твёрдой поверхности, находящейся в контакте с газом (паром) или другой жидкостью, пропитывании пористых тел и порошков, искривлении поверхности жидкости у поверхности твёрдого тела. Так, Смачивание вызывает образование сферического мениска в капиллярной трубке, определяет форму капли на твёрдой поверхности или форму газового пузырька, прилипшего к поверхности погруженного в жидкость тела. Смачивание часто рассматривают как результат межмолекулярного (вандерваальсова) взаимодействия в зоне контакта трёх фаз (тел, сред). Однако во многих случаях, например при соприкосновении жидких металлов с твёрдыми металлами, окислами, алмазом, графитом, Смачивание обусловлено не столько межмолекулярным взаимодействием, сколько образованием химических соединений, твёрдых и жидких растворов, диффузионными процессами в поверхностном слое смачиваемого тела. , где
, где  - плотность воды, h - разность уровней воды в сосудах А и В. Это значит, что искривленный поверхностный слой жидкости создал добавочное давление под своей выпуклой поверхностью. Добавочное давление тем больше, чем меньше радиус кривизны этой поверхности. При попытке дальнейшего опускания трубки, вода будет из нее вытекать.Если конец трубки В поднять выше уровня воды в сосуде А (рис.в), то поверхность воды в трубке В станет вогнутой (вода смачивает стекло) и уровень воды в трубке В будет выше уровня воды в сосуде А. Это означает, что под искривленной поверхностью воды в трубке В давление меньше атмосферного.Отсюда следует вывод: давление непосредственно под выпуклой поверхностью жидкости больше давления под плоской поверхностью жидкости, а давление под вогнутой поверхностью жидкости меньше давления, чем под плоской поверхностью.
- плотность воды, h - разность уровней воды в сосудах А и В. Это значит, что искривленный поверхностный слой жидкости создал добавочное давление под своей выпуклой поверхностью. Добавочное давление тем больше, чем меньше радиус кривизны этой поверхности. При попытке дальнейшего опускания трубки, вода будет из нее вытекать.Если конец трубки В поднять выше уровня воды в сосуде А (рис.в), то поверхность воды в трубке В станет вогнутой (вода смачивает стекло) и уровень воды в трубке В будет выше уровня воды в сосуде А. Это означает, что под искривленной поверхностью воды в трубке В давление меньше атмосферного.Отсюда следует вывод: давление непосредственно под выпуклой поверхностью жидкости больше давления под плоской поверхностью жидкости, а давление под вогнутой поверхностью жидкости меньше давления, чем под плоской поверхностью.
 где l - длина участка впитавшейся жидкости, h - ее вязкость, Dp - перепад давления на участке l, равный капиллярному давлению мениска: Dp = — 2s12cos q/r. Если краевой угол q не зависит от скорости v, можно рассчитать кол-во впитавшейся жидкости за время t из соотношения: l(t) = (rts12cos q/2h)l/2. (5) Ур-ния (4) и (5) используют для расчетов скорости пропитки при обработке древесины антисептиками, крашении тканей, нанесении катализаторов на пористые носители, выщелачивании и диффузионном извлечении ценных компонентов горных пород и др. Формула Лапласа:
где l - длина участка впитавшейся жидкости, h - ее вязкость, Dp - перепад давления на участке l, равный капиллярному давлению мениска: Dp = — 2s12cos q/r. Если краевой угол q не зависит от скорости v, можно рассчитать кол-во впитавшейся жидкости за время t из соотношения: l(t) = (rts12cos q/2h)l/2. (5) Ур-ния (4) и (5) используют для расчетов скорости пропитки при обработке древесины антисептиками, крашении тканей, нанесении катализаторов на пористые носители, выщелачивании и диффузионном извлечении ценных компонентов горных пород и др. Формула Лапласа: 



