Соотношение взаимности Максвелла и их значение.
Метод термодинамических потенциалов помогает преобразовывать выражения, в которые входят основные термодинамические переменные и тем самым выражать такие «труднонаблюдаемые» величины, как количество теплоты, энтропию, внутреннюю энергию через измеряемые величины — температуру, давление и объём и их производные. Рассмотрим опять выражение для полного дифференциала внутренней энергии:
Известно, что если смешанные производные существуют и непрерывны, то они не зависят от порядка дифференцирования, то есть
Но
Рассматривая выражения для других дифференциалов, получаем:
Эти соотношения называются соотношениями Максвелла. Заметим, что они не выполняются в случае разрывности смешанных производных, что имеет место при фазовых переходах 1-го и 2-го рода.
Соотношения Максвелла. Все термодинамические потенциалы являются функциями состояния системы. Зная любой из четырех потенциалов как функцию естественных переменных, можно с помощью основного уравнения термодинамики найти все другие термодинамические функции и параметры системы. Для этого используют соотношения между частными производными, которые называют соотношениями Максвелла (таблица). Например, для
Другие из уравнений, называемых соотношениями Максвелла, получают аналогичным образом.
|
.
.
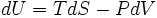и 
, поэтому
.
,
,
.
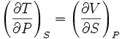соответствующее уравнение получают следующим образом:
= 
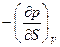(61)
= 
= 
= 
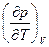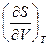
