ЭНТРОПИЯ КАК ФУНКЦИЯ СОСТОЯНИЯ.
Энтропия - понятие, для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:
Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию. Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
где dS — приращение (дифференциал) энтропии, а δQ — бесконечно малое приращение количества теплоты. Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия). Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому δQ считать полным дифференциалом нельзя. Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю. Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
Термин широко применяется и в других областях знания: в статистической физике — как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса). 27.ФОРМУЛИРОВКА ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ С ИСПОЛЬЗОВАНИЕМ ПОНЯТИЯ ЭНТРОПИЯ. ТЕРМОДИНАМИЧЕСКИЙ СМЫСЛ ЭНТРОПИИ. Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T: Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию. Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:
где dS — приращение (дифференциал) энтропии, а δQ — бесконечно малое приращение количества теплоты. Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия). Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому δQ считать полным дифференциалом нельзя. Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю. 28.СТАТИСТИЧЕСКИЙ СМЫСЛ ЭНТРОПИИ. Ф-ЛА БОЛЬЦМАНА.
|



 неравно
неравно  неравно
неравно  такие отклонения чисел
такие отклонения чисел  от средних значений обусловлено тепловым движением, которое назыв. флуктуациями. Рассчитаем вероятность таких процессов очевидно если количество молекул в сосуде N=1,то Р=
от средних значений обусловлено тепловым движением, которое назыв. флуктуациями. Рассчитаем вероятность таких процессов очевидно если количество молекул в сосуде N=1,то Р=  ; N=2,то Р=
; N=2,то Р=  , вероятность того что частица V0/V, V0- та часть сосуда в котором мы ожидаем видеть частицы, V-весь объём, Р
, вероятность того что частица V0/V, V0- та часть сосуда в котором мы ожидаем видеть частицы, V-весь объём, Р 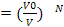 . Относительно большие флуктуации встречаются в системах с малым числом частиц, система с большим числом частиц флуктуации практически не встречаются, следовательно энтропия самостоятельно стремится в состояние с большей энтропией. Рассм. Две подсистемы с вероятными
. Относительно большие флуктуации встречаются в системах с малым числом частиц, система с большим числом частиц флуктуации практически не встречаются, следовательно энтропия самостоятельно стремится в состояние с большей энтропией. Рассм. Две подсистемы с вероятными 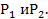
 =f(
=f( ,
,  =f(
=f(
 , тогда
, тогда  , f(
, f( = f(
= f( , то и f(
, то и f( d f(
d f(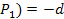 f(
f( =
=  .
.  =
=  . K=const, тогда P
. K=const, тогда P 
 , f=kln
, f=kln  . S=k ln P-раз это ф-ла справедлива для любой системы значит справедлива для идеального газа. Рассм процесс изотермический перехода идеального газа из состояния 1 в 2, ΔS=
. S=k ln P-раз это ф-ла справедлива для любой системы значит справедлива для идеального газа. Рассм процесс изотермический перехода идеального газа из состояния 1 в 2, ΔS=  =k(ln
=k(ln  )=Rln
)=Rln  т.к.
т.к.  ,
,  ; Rln
; Rln  =kln
=kln  , R=k
, R=k  . S=klnG- формула Больцмана.
. S=klnG- формула Больцмана.


