Изобарический
В изобарическом процессе (P = const):
δQ = dU + PdV = νCVΔT + νRΔT = ν(CV + R)ΔT = νCPΔT
CP=δQ/νΔT=CV+R=(1+i/2)*R
17.Первое начало термодинамики и его различные формулировки
Закон представляет формулировку принципа сохранения энергии для термодинамических систем. Он формулируется следующим образом: При переходе системы из состояния A в состояние B сумма работы и теплоты, полученных системой от окружающей среды, определяется только состояниями A и B; эта сумма не зависит от того, каким способом осуществляется переход из A в B. Это означает, что существует такая величина E, характеризующая внутреннее состояние системы, что разность ее значений в состояниях A и B определяется соотношением
где (– L) – работа, совершенная средой над системой, а Q – количество тепла, полученное системой от окружающей среды (количество энергии, передаваемое системе термическим образом, т.е. в форме, отличной от работы). Для бесконечно малого изменения состояния
или, используя выражение для δ L,
Таким образом, изменение внутренней энергии системы равно сумме полученного тепла и совершенной над системой работы. (1) Пример: Рассмотрим систему, состоящую из определенного количества воды в сосуде. Энергию системы можно увеличить двумя путями. Первый: можно нагревать сосуд на огне. При этом объем воды почти не увеличивается, т.е. dV = 0 и, следовательно, работа не производится. Второй путь: опустим в воду установку с вращающимися лопастями и путем трения увеличим температуру воды до того же значения, что и в первом случае. Конечные состояния системы и приращения ее энергии в обоих случаях одни и те же, но во втором случае увеличение энергии обусловлено работой. Эквивалентность теплоты и механической работы становится особенно ясной, если рассмотреть циклический процесс. Так как начальное и конечное состояния цикла одинаковы, то изменение энергии равно нулю (EA = EB) и, следовательно,
т.е. работа, совершенная системой во время цикла, равна количеству теплоты, поглощенному системой. (4) Теплота измеряется в единицах энергии – эргах, джоулях и калориях. Соотношение между джоулем и калорией имеет вид
Это – механический эквивалент теплоты. Величины Q и L не являются функциями состояния системы; они зависят от способа перехода из состояния А в В. Соответственно этому δ Q и δ L не являются полными дифференциалами. Это обстоятельство и отмечается использованием символа δ;, а не d. (1)
Применим первый закон к системам типа однородной жидкости, состояния которых определяются двумя из трех переменных P, V и T. В этом случае любая функция состояния системы и, в частности, внутренняя энергия E будет функцией двух переменных, выбранных в качестве независимых. Чтобы избежать неправильного толкования того, какая переменная является независимой при вычислении частной производной, будем заключать символ частной производной в скобки и помещать внизу скобок ту величину, которая при частном дифференцировании остается постоянной. Таким образом,
означает частную производную E по T при постоянном V; причем T и V взяты в качестве независимых переменных. Эта производная отличается от частной производной (∂ E /∂ T) P, при взятии которой остается постоянным давление P. (3) Рассмотрим теперь бесконечно малый процесс, т.е. процесс, при котором независимые переменные изменяются на бесконечно малые величины. Для такого процесса 1-й закон термодинамики можно переписать в виде
Если в качестве независимых взять переменные T и V, то E = E (T, V) и, следовательно,
Соотношение принимает тогда вид:
Если считать независимыми переменными T и P, то
и принимает вид
Теплоемкость тела определяется как отношение бесконечно малого количества поглощенной теплоты к бесконечно малому изменению температуры, вызванному этой теплотой. Очевидно, что величина теплоемкости зависит от того, нагревается ли тело при постоянном объеме или при постоянном давлении. Обозначим символами cV и cP теплоемкости при постоянном объеме и при постоянном давлении соответственно. Поскольку при V = const, dV = 0, то
Подобным же образом из (8) получается выражение для cP:
Второй член в формуле для cP связан со слагаемым PdV, т.е. описывает эффеккт, оказываемый на теплоемкость работой, которую система совершает во время расширения. В (9) подобного члена нет, поскольку объем остается постоянным и работа не совершается. (1) Во многих случаях удобно пользоваться понятием молярной теплоемкости. Молярной теплоемкостью называется теплоемкость одного моля вещества. Молярные теплоемкости при постоянном V и при постоянном P определяются формулами (9) и (10), если вместо произвольного количества вещества взять 1 моль:
знак
В случае газа можно конкретизировать зависимость внутренней энергии E от переменных T и V, определяющих его состояние. В дальнейшем мы докажем, что энергия идеального газа определяется температурой T и не зависит от объема V: E = E (T). Для реальных газов это утверждение выполняется приближенно. Для определения зависимости E (T) воспользуемся результатами опыта, согласно которым теплоемкость газов очень слабо зависит от температуры. Можно предположить, что для идеального газа она строго постоянна. Тогда интегрирование уравнения
при условии CV = const дает:
где E 0– константа, представляющая энергию газа при абсолютном нуле.
Для идеального газа 1-й закон термодинамики принимает вид
Из этого уравнения легко получить соотношение между молярными теплоемкостями CV и CP. Для этого перейдем от переменных T и V к переменным T и P. Это можно сделать, если взять дифференциалы от обеих частей уравнения состояния для 1 моля идеального газа
что дает
Выражая отсюда
Отсюда можно легко найти CP. Поскольку при P = const дифференциал dP = 0, то
т.е. разность между молярными теплоемкостями газа при постоянном давлении и при постоянном объеме равна газовой постоянной R. (1)
Литература: 4.Билимович Б.Ф. Тепловые явления в технике1981г.
|






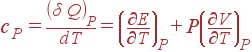
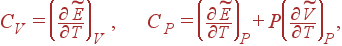
 сверху означает, что взят 1 моль вещества. (2)
сверху означает, что взят 1 моль вещества. (2)



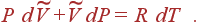
 и подставляя в (15), получаем
и подставляя в (15), получаем




