Основные теоретические положения
Трехфазная сеть, как правило, представлена симметричными, т. е. равными по абсолютному значению напряжениями со взаимным сдвигом по фазе на 120°. Для включения электроприемников (нагрузки) в сеть трехфазного тока их соединяют звездой или треугольником. При включении нагрузки звездой (рис. 5) концы фаз, соединенные вместе, образуют нулевую точку, к которой может быть подключен провод, называемый нейтральным. В этом случае имеем четырехпроводную схему, в которой к потребителю подводятся линейные и фазные напряжения сети (если пренебречь сопротивлением соединительных проводов):
В общем случае линейные напряжения
Если сопротивления нагрузки отдельных фаз равны между собой, т. е. za = zb = zc, то такая нагрузка называется равномерной, тогда для линейных и фазных напряжений имеет место следующее соотношение: Векторная диаграмма напряжений и токов при равномерной активной нагрузке, соединенной звездой, представлена на рис. 6, а. При равномерной нагрузке фаз сумма мгновенных значений тока всех фаз или геометрическая сумма векторов каждого тока равна нулю. Ток в нулевом проводе будет отсутствовать, следовательно, при равномерной нагрузке нет необходимости его подключать. Схема в этом случае становится трехпроводной.
а б Рис. 6. Векторные диаграммы напряжений и токов при равномерной (а) и неравномерной (б) активной нагрузке фаз, соединенных звездой с нулевым проводом
Неравномерная нагрузка, соединенная звездой, обычно подключается по четырехпроводной схеме, т. е. с нулевым проводом, так как при наличии нулевого провода, обладающего малым сопротивлением, неравномерная нагрузка не приводит к значительному изменению фазных напряжений. Можно считать, что фазные напряжения при неравномерной нагрузке остаются такими же, как и для случая равномерной нагрузки:
По нулевому проводу будет протекать уравнительный ток I 0, при этом сумма всех токов Векторная диаграмма при неравномерной нагрузке фаз, соединенных звездой с нулевым проводом, представлена на рис. 6, б. Отсутствие нулевого провода при неравномерной нагрузке нарушает нормальный режим работы установки. Фазные токи изменяются и устанавливаются так, чтобы их сумма была равна нулю. В результате этого происходит искажение симметрии фазных напряжений: фаза с меньшим сопротивлением оказывается по сравнению с нормальным под сниженным напряжением, а с большим сопротивлением – под повышенным. Векторная диаграмма при отсутствии нулевого провода и неравномерной нагрузке представлена на рис. 7. Мощность, потребляемая нагрузкой, для любого режима
где
При включении потребителей треугольником (рис. 8) фазные нагрузки подключаются на линейные напряжения, а поэтому фазные напряжения равны линейным: Линейный ток каждой фазы равен разности токов примыкающих фаз (геометрическая разность векторов фазных токов):
Векторная диаграмма напряжений и токов при равномерной активной нагрузке представлена на рис. 9. В этом случае линейные и фазные токи связаны между собой соотношением:
При неравномерной нагрузке фаз соотношение (31) нарушается. Векторная диаграмма токов становится несимметричной (рис. 10), т. е. линейные провода загружаются неодинаково. Например, изменение нагрузки в одной из фаз влияет на изменение двух линейных токов и не влияет на величины фазных напряжений и токов двух других фаз, а также третьего линейного тока.
При обрыве одного из линейных проводов, например С (рис. 11, а), нормальный режим работы установки нарушается. Потребители фазы А будут находиться под нормальным фазным напряжением U ф, а потребители фаз В и С окажутся последовательно соединенными и будут питаться от этого же напряжения. В этом случае линейный ток
так как В данном режиме работы трехфазной цепи соотношение токов
если Фазное напряжение Мощность, потребляемая симметричной нагрузкой при соединении звездой и треугольником, определяется по одним и тем же формулам:
или
 . (35) . (35)
а б Рис. 11. Схема (а) и векторная диаграмма напряжений и токов (б) при обрыве линейного провода
|

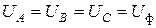 ; (23а)
; (23а)
 . (23б)
. (23б)
 ,
,  ,
,  связаны с фазными
связаны с фазными  ,
,  ,
,  следующими уравнениями:
следующими уравнениями: (24)
(24)




 При соединении нагрузки звездой ток в подводящих проводах будет одновременно и током фазы: I л = I ф.
При соединении нагрузки звездой ток в подводящих проводах будет одновременно и током фазы: I л = I ф. .
.
 . (25)
. (25) .
. , (26)
, (26) ,
,  ,
,  - мощность фаз A, B, C.
- мощность фаз A, B, C. Активная мощность каждой фазы
Активная мощность каждой фазы . (27)
. (27) .
. ; (28)
; (28) ; (29)
; (29) . (30)
. (30)
 . (31)
. (31) Рис. 9. Векторная диаграмма напряжений и токов при равномерной нагрузке
Рис. 9. Векторная диаграмма напряжений и токов при равномерной нагрузке
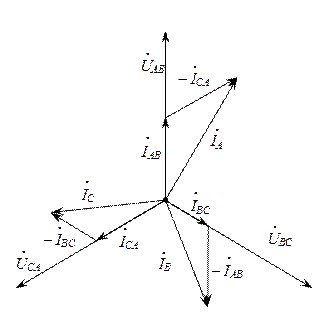 Рис. 10. Векторная диаграмма напряжений и токов при неравномерной
нагрузке
Рис. 10. Векторная диаграмма напряжений и токов при неравномерной
нагрузке
 равен току
равен току  по первому закону Кирхгофа:
по первому закону Кирхгофа: , (32)
, (32) .
. и
и  в обеих ветвях будет обратно пропорционально сопротивлениям этих ветвей:
в обеих ветвях будет обратно пропорционально сопротивлениям этих ветвей: , (33)
, (33) , то фазный ток
, то фазный ток  по-прежнему будет равно линейному
по-прежнему будет равно линейному  , а фазные напряжения
, а фазные напряжения  и
и  будут равны между собой и равны половине линейного
будут равны между собой и равны половине линейного  =
= 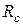 ) (рис. 11, б).
) (рис. 11, б). (34)
(34)



