Основные теоретические положения. В последовательной цепи переменного тока, в которую включены реостат R, катушка индуктивности L и конденсатор С
В последовательной цепи переменного тока, в которую включены реостат R, катушка индуктивности L и конденсатор С, возможен случай, когда индуктивное сопротивление катушки хL равно емкостному сопротивлению конденсатора хC. Индуктивное сопротивление катушки определяется по выражению:
емкостное сопротивление конденсатора –
Полное сопротивление цепи
где Если выполняется равенство реактивных сопротивлений: х L= хC, то ток в цепи практически определяется только активным сопротивлением (
Если активное сопротивление минимально, то ток в цепи достигает больших значений. При этом падение напряжения на катушке U к = (хL +
Режим, когда хL = хC и ток совпадает по фазе с напряжением, приложенным к цепи, называется резонансом напряжений. Резонанс напряжений может наступить, если выполняется следующее: 1) при постоянной индуктивности емкость С меняется и становится равной 1 / ω2 L, где ω = 2πƒ; 2) при постоянной емкости индуктивность L меняется и становится равной 1/ω2 С; 3) изменение индуктивности L и емкости С приводит к равенству: ω L = l/ω C; 4) угловая частота сети w0, изменяясь, становится равной В лабораторной работе наступления резонанса напряжений добиваемся подбором емкости. Кроме резонанса напряжений необходимо исследовать еще два режима, когда х L > хС и хL < хC. Для всех трех режимов необходимо построить векторные диаграммы напряжения и тока. Для этого следует измерить ток I в цепи и напряжение на конденсаторе UC, катушке U к и реостате UR и рассчитать значения сопротивлений xL, xС , Расчет величин, перечисленных выше, проводим по известным формулам: полное сопротивление цепи z = U/I; полное сопротивление катушки z к = U к/ I; реактивное сопротивление конденсатора xC = UC / I; активное сопротивление всей цепи R общ = P/I2; активное сопротивление реостата R = UR / I; активное сопротивление катушки r к = R общ – R; реактивное сопротивление катушки Зная xL, определим индуктивность, Гн:
По реактивному сопротивлению конденсатора xC рассчитаем емкость, мкФ:
Вычислим угол сдвига между током и напряжением:
Порядок построения упрощенных векторных диаграмм: 1) чертится ось токов, совпадающая с осью абсцисс (рис. 1);
3) из конца вектора 4) из начала вектора тока радиусом, равным приложенному к цепи напряжению 5) из конца вектора 6) точка пересечения засечек соединяется вектором Векторные диаграммы построить для случаев: xL > xС; xL = xС; xL < xС.
|

 , (1)
, (1) . (2)
. (2) (3)
(3) , R – активное сопротивление катушки и реостата.
, R – активное сопротивление катушки и реостата. (4)
(4)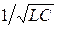 (этого можно добиться, изменяя частоту ƒ питающей сети).
(этого можно добиться, изменяя частоту ƒ питающей сети).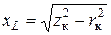 .
. (5)
(5)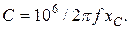 (6)
(6) . (7)
. (7) 2) из начала вектора тока откладывается в выбранном масштабе вектор напряжения
2) из начала вектора тока откладывается в выбранном масштабе вектор напряжения  , совпадающий с вектором тока по направлению, так как падение напряжения на активном сопротивлении совпадает по фазе с током;
, совпадающий с вектором тока по направлению, так как падение напряжения на активном сопротивлении совпадает по фазе с током;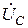 , так как емкостное напряжение отстает по фазе от тока на угол 90°;
, так как емкостное напряжение отстает по фазе от тока на угол 90°; , делается засечка;
, делается засечка; , делается вторая засечка;
, делается вторая засечка;


