Системы линейных уравнений. Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида
Раздел 5. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Основные понятия Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида
где числа аij, i= Такую систему удобно записывать в компактной матричной форме Здесь А – матрица коэффициентов системы, называемая основной матрицей:
Расширенной матрицей системы называется матрица
Решением системы называется п значений неизвестных х1=с1, х2=с2,..., хп=сп, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему – это значит выяснить, совместна она или не совместна. Если система совместна, то найти ее общее решение. Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот. Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как х1=х2=…=хп=0 является решением системы. Это решение называется нулевым или тривиальным. Решение систем линейных уравнений Пусть дана произвольная система т линейных уравнений с п неизвестными
Теорема 1 (Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы. Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений. П р и м е р. Исследовать на совместность систему Решение. Таким образом, r (A)¹ r (
Решение невырожденных систем линейных уравнений. Формулы Крамера Пусть дана система п линейных уравнений с п неизвестными
или в матричной форме А∙Х=В. Основная матрица А такой системы – квадратная. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной. Найдем решение данной системы уравнений в случае ∆¹0. умножив обе части уравнения А∙Х=В слева на матрицу А-1, получим А-1∙ А∙Х= А-1∙В. Поскольку А-1∙ А=Е и Е∙Х=Х, то Х= А-1∙ В. Данный способ решения системы называют матричным. Из матричного способа вытекают формулы Крамера П р и м е р. Решить систему Решение. Решение систем линейных уравнений методом Гаусса Метод Гаусса состоит в последовательном исключении неизвестных. Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
где k ≤ п, аii ¹ 0, i= На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы. Замечания: 1. Если ступенчатая система оказывается треугольной, т.е. k=n, то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения находим хп-1, далее поднимаясь по системе вверх, найдем все остальные неизвестные. 2. На практике удобнее работать с расширенной матрицей системы, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент а11 был равен 1(уравнения переставить местами, либо разделить на а11 ¹1). П р и м е р. Решить систему методом Гаусса Решение. В результате элементарных преобразований над расширенной матрицей системы
~ исходная система свелась к ступенчатой: Поэтому общее решение системы: x2=5x4 -13x3 -3; x1=5x4 -8x3 -1. Если положить, например, х3=х4=0, то найдем одно из частных решений этой системы х1=-1, х2=-3, х3=0, х4=0. Систем однородных линейных уравнений Пусть дана система линейных однородных уравнений
Очевидно, что однородная система всегда совместна, она имеет нулевое (тривиальное) решение. Теорема 4. Для того, чтобы система однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е. r<n. Теорема 5. Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевое решение, необходимо и достаточно, чтобы определитель ее основной матрицы был равен нулю, т.е. ∆=0. Если система имеет ненулевые решения, то ∆=0. П р и м е р. Решить систему Решение.
Положив х3=0, получим одно частное решение: х1=0, х2=0, х3=0. Положив х3=1, получим второе частное решение: х1=2, х2=3, х3=1 и т.д. Вопросы для контроля ü Что такое система линейных алгебраических уравнений? ü Поясните следующие понятия: коэффициент, свободный член, основная и расширенная матрицы. ü Какими бывают системы линейных уравнений? Сформулируйте теорему Кронкера-Капелли (о совместности системы линейных уравнений). ü Перечислите и поясните методы решения систем линейных уравнений.
|


 , j=
, j=  называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа хп.
называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа хп. .
. ,
, – вектор-столбец из неизвестных хj,
– вектор-столбец из неизвестных хj,  – вектор-столбец из свободных членов bi.
– вектор-столбец из свободных членов bi. системы, дополненная столбцом свободных членов
системы, дополненная столбцом свободных членов .
. .
.

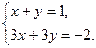
 , r(A)=1;
, r(A)=1;  , r(
, r( .
.
 , где ∆ – определитель основной матрицы системы, а ∆ i – определитель, полученный из определителя ∆ путем замены i -го столбца коэффициентов столбцом из свободных членов.
, где ∆ – определитель основной матрицы системы, а ∆ i – определитель, полученный из определителя ∆ путем замены i -го столбца коэффициентов столбцом из свободных членов.
 , 7¹0,
, 7¹0,  ,
,  . Значит, х1=
. Значит, х1=  , х2=
, х2= 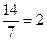 .
.
 . Коэффициенты аii называются главными элементами системы.
. Коэффициенты аii называются главными элементами системы.
 ~
~  ~
~  ~
~

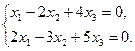
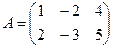 , r(A)=2
, r(A)=2  , п=3. Так как r<n, то система имеет бесконечное множество решений.
, п=3. Так как r<n, то система имеет бесконечное множество решений.
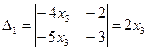 ,
,  . Стало быть, х1=
. Стало быть, х1=  =2х3, х2=
=2х3, х2= 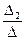 =3х3 – общее решение.
=3х3 – общее решение.


