We have to be careful the converse is not true. Indeed, the improper integral

is convergent while the improper integral
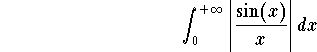
is divergent. This is quite hard to show. On the other hand, it shows that the convergence of  carries more information than just convergence. In this case, we say that the improper integral
carries more information than just convergence. In this case, we say that the improper integral  is absolutely convergent. And if the improper integral
is absolutely convergent. And if the improper integral  is convergent while the improper integral
is convergent while the improper integral  is divergent, we say it is conditionally convergent.
is divergent, we say it is conditionally convergent.
Example. Establish the convergence or divergence of

Answer. We have an improper integral of Type II. Since the function  is not positive on
is not positive on  , we will investigate whether the given improper integral is absolutely convergent. Hence we must consider the improper integral
, we will investigate whether the given improper integral is absolutely convergent. Hence we must consider the improper integral

Let us check whether we have a Type I behavior. Clearly the point 0 is a bad point. We leave it as an exercise to check that the function 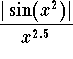 is indeed unbounded around 0. So we must split the integral and write
is indeed unbounded around 0. So we must split the integral and write
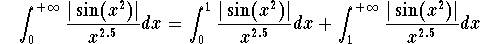
First let us take care of the integral

We know that  when
when  . Hence we have
. Hence we have
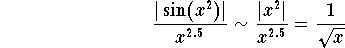
when  . Since the integral
. Since the integral  is convergent via the p-test, the limit test enables us to conclude that the integral
is convergent via the p-test, the limit test enables us to conclude that the integral

is convergent. Next we take care of the improper integral

We can not use the limit test since the function  does not have a nice behavior around
does not have a nice behavior around 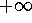 . But we know that
. But we know that  for any number x. Hence we have
for any number x. Hence we have

for any  . Since the improper integral
. Since the improper integral  is convergent via the p-test, the basic comparison test implies that the improper integral
is convergent via the p-test, the basic comparison test implies that the improper integral

is convergent. Therefore putting the two integrals together, we conclude that the improper integral

is convergent. This clearly implies that the improper integral

is absolutely convergent.
Example. Show that the improper integral

is convergent.
Answer. As we mentioned before, this improper integral is not absolutely convergent. So there is no need of considering the absolute value of the function. Note that the integral is improper obviously because of 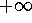 . 0 is not a bad point since
. 0 is not a bad point since

But even if it is not a bad point, we will isolate it by writing
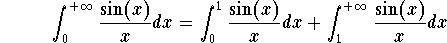
The integral  is not improper. So we concentrate on the integral
is not improper. So we concentrate on the integral

We know by definition that
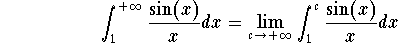
Now consider the proper integral  . An integration by parts gives
. An integration by parts gives
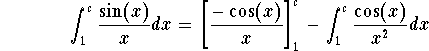
Since
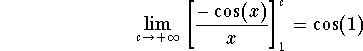
and

we get
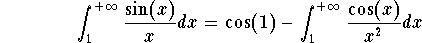
Note now that the improper integral  is in fact absolutely convergent. Indeed, we have
is in fact absolutely convergent. Indeed, we have

and since by the p-test the improper integral  is convergent, the basic comparison test implies the desired conclusion, that is
is convergent, the basic comparison test implies the desired conclusion, that is 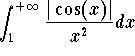 is convergent. Therefore the improper integral
is convergent. Therefore the improper integral  is convergent. Since
is convergent. Since
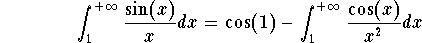
then the improper integral  is convergent.
is convergent.
Интеграл Фурье
Пусть  определена на бесконечном промежутке (-∞,+∞) удовлетворяет следующим условиям:
определена на бесконечном промежутке (-∞,+∞) удовлетворяет следующим условиям:
1)  несобственный интеграл
несобственный интеграл  это свойство
это свойство  называется её абсолютной интегрируемостью) на всей вещественной оси.
называется её абсолютной интегрируемостью) на всей вещественной оси.
2) На  конечном сегменте
конечном сегменте  представима в виде суммы своего ряда Фурье. (Практически требуют, чтобы
представима в виде суммы своего ряда Фурье. (Практически требуют, чтобы  на
на  конечном сегменте удовлетворяла условиям Дирихле и была непрерывной.)
конечном сегменте удовлетворяла условиям Дирихле и была непрерывной.)
Построим для  на (
на ( ) разложение аналогичное в некотором смысле разложению в ряд Фурье периодической функции.
) разложение аналогичное в некотором смысле разложению в ряд Фурье периодической функции.
Если эти условия выполнены, мы можем рассуждать следующим образом.
Фиксируем некоторое произвольное  и напишем разложение функции в ряд Фурье на
и напишем разложение функции в ряд Фурье на  .
.
(1) 
(2) 
Подставляем в ряд (1) выражения для коэффициентов (2).

Последнее выражение имеет место для всех  где
где  число.
число.
Пусть  я фиксированная (.)
я фиксированная (.)  .
.
Рассмотрим предел полученного выражение при  . Докажем, что
. Докажем, что
 т.к.
т.к.  сходится, то его частные интегралы ограничены, т.е.
сходится, то его частные интегралы ограничены, т.е.  что
что  т.к.:
т.к.:
 откуда
откуда  таким образом имеем:
таким образом имеем: 
Вводя зависимую от “n” переменную,  последовательность, и полагая
последовательность, и полагая 

 при
при 

эта сумма (последняя) напоминает интегральную сумму.
С ростом  число слагаемых увеличивается, а каждое слагаемое уменьшается. Поэтому естественно, предполагать, что при возрастании
число слагаемых увеличивается, а каждое слагаемое уменьшается. Поэтому естественно, предполагать, что при возрастании  эта сумма стремится к интегралу по “U” (строгого доказательства этого факта мы не приводим).
эта сумма стремится к интегралу по “U” (строгого доказательства этого факта мы не приводим).

(3)  это двойной интеграл Фурье.
это двойной интеграл Фурье.
Преобразуем правую часть (3).
 в U.
в U.
(4) 
(5) 
Равенство (3) доказано в точках непрерывности и следовательно, можно сформулировать достаточные условия разложимости функции в виде (3).
Th. Если:
1)  - абсолютно интегрируема
- абсолютно интегрируема
2) На  конечном сегменте
конечном сегменте  она удовлетворяет условию Дирихле, то в точках непрерывности имеет место представление (3).
она удовлетворяет условию Дирихле, то в точках непрерывности имеет место представление (3).
Замечание. Несобственные интегралы в формулах (4) и (5) понимаются в смысле главного значения, т.е.  и обозначают через
и обозначают через
V.P. 
Df. Пусть функция  определена на
определена на  и
и  Пусть
Пусть  Тогда этот предел называется главным значением (по Коши) интеграла
Тогда этот предел называется главным значением (по Коши) интеграла 
Обозначение: 
Замечание. Если  Н.И.
Н.И.  то очевидно,
то очевидно,  и главное значение
и главное значение  причём
причём 
Аналогично вводится понятие главного значения интеграла в изолированной особой точке  функции
функции 

Пример 1. Н.И.  не
не  , но
, но  поэтому имеем
поэтому имеем 
Пример 2. Н.И.  не
не  , но
, но  имеем
имеем  так, что
так, что 


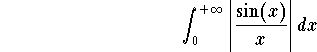
 carries more information than just convergence. In this case, we say that the improper integral
carries more information than just convergence. In this case, we say that the improper integral  is absolutely convergent. And if the improper integral
is absolutely convergent. And if the improper integral 
 is not positive on
is not positive on  , we will investigate whether the given improper integral is absolutely convergent. Hence we must consider the improper integral
, we will investigate whether the given improper integral is absolutely convergent. Hence we must consider the improper integral
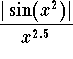 is indeed unbounded around 0. So we must split the integral and write
is indeed unbounded around 0. So we must split the integral and write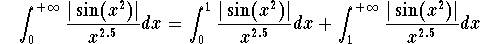

 when
when  . Hence we have
. Hence we have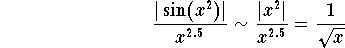
 . Since the integral
. Since the integral  is convergent via the p-test, the limit test enables us to conclude that the integral
is convergent via the p-test, the limit test enables us to conclude that the integral
 does not have a nice behavior around
does not have a nice behavior around  . But we know that
. But we know that  for any number x. Hence we have
for any number x. Hence we have
 . Since the improper integral
. Since the improper integral  is convergent via the p-test, the basic comparison test implies that the improper integral
is convergent via the p-test, the basic comparison test implies that the improper integral
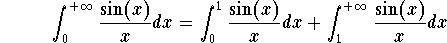
 is not improper. So we concentrate on the integral
is not improper. So we concentrate on the integral
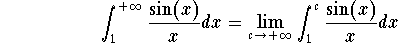
 . An integration by parts gives
. An integration by parts gives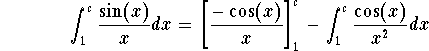
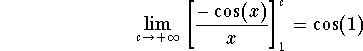

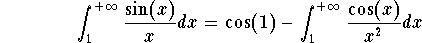
 is in fact absolutely convergent. Indeed, we have
is in fact absolutely convergent. Indeed, we have
 is convergent, the basic comparison test implies the desired conclusion, that is
is convergent, the basic comparison test implies the desired conclusion, that is 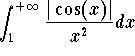 is convergent. Therefore the improper integral
is convergent. Therefore the improper integral  is convergent.
is convergent. определена на бесконечном промежутке (-∞,+∞) удовлетворяет следующим условиям:
определена на бесконечном промежутке (-∞,+∞) удовлетворяет следующим условиям: несобственный интеграл
несобственный интеграл  это свойство
это свойство  конечном сегменте
конечном сегменте  ) разложение аналогичное в некотором смысле разложению в ряд Фурье периодической функции.
) разложение аналогичное в некотором смысле разложению в ряд Фурье периодической функции. и напишем разложение функции в ряд Фурье на
и напишем разложение функции в ряд Фурье на  .
.


 где
где  число.
число. я фиксированная (.)
я фиксированная (.)  .
. . Докажем, что
. Докажем, что т.к.
т.к.  сходится, то его частные интегралы ограничены, т.е.
сходится, то его частные интегралы ограничены, т.е.  что
что  т.к.:
т.к.: откуда
откуда  таким образом имеем:
таким образом имеем: 
 последовательность, и полагая
последовательность, и полагая 

 при
при 

 число слагаемых увеличивается, а каждое слагаемое уменьшается. Поэтому естественно, предполагать, что при возрастании
число слагаемых увеличивается, а каждое слагаемое уменьшается. Поэтому естественно, предполагать, что при возрастании 
 это двойной интеграл Фурье.
это двойной интеграл Фурье. в U.
в U.

 она удовлетворяет условию Дирихле, то в точках непрерывности имеет место представление (3).
она удовлетворяет условию Дирихле, то в точках непрерывности имеет место представление (3). и обозначают через
и обозначают через
 определена на
определена на  и
и  Пусть
Пусть  Тогда этот предел называется главным значением (по Коши) интеграла
Тогда этот предел называется главным значением (по Коши) интеграла 

 то очевидно,
то очевидно,  причём
причём 
 функции
функции 

 не
не  поэтому имеем
поэтому имеем 
 не
не  имеем
имеем  так, что
так, что 



