Анализ достоверности модели
После построения модели необходимо выполнить проверку ее адекватности. Оценка адекватности модели производится на основании анализа значения коэффициента корреляции r, вычисляемым по формуле:
где
Его величина может изменяться в пределах отрезка от –1 до 1. Чем ближе к единице модуль значения коэффициента корреляции, тем теснее линейная связь между х и у. При полном отсутствии связи r = 0, при | r | < 0.5 гипотеза о наличии линейной связи отвергается, и линейная модель признается неадекватной. Что касается диапазона значений модуля коэффициента от 0.5 до 1, то минимальный предел значения модуля r, при котором модель признается адекватной, определяется требованиями к точности модели – чем выше требования, тем ближе этот предел к единице. Помимо оценки тесноты связи, коэффициент корреляции позволяет судить о характере зависимости между величинами х и у: если r > 0, между х и у имеет место положительная корреляционная связь, т. е. с ростом параметра х увеличивается параметр у; если r < 0, между х и у имеет место отрицательная связь. Мерой ошибки регрессионной модели служит среднее квадратичное отклонение (стандартное отклонение), которое рассчитывается по формуле:
Для оценки надежности полученного результата используют иногда критерий надежности m, который учитывает как величину коэффициента корреляции, так и число пар измерений. Критерий надежности m рассчитывается по формуле
где r– коэффициент корреляции; т– число пар измерений. Как видно из формулы критерия надежности, чем выше коэффициент корреляции и большее число пар измерений, тем больше показатель надежности. При m > 2,6 связь считается статистически достоверной.
|

 , (2.9)
, (2.9)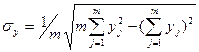 ; (2.10)
; (2.10)  . (2.11)
. (2.11) . (2.12)
. (2.12) , (2.13)
, (2.13)


