РЕГРЕССИОННЫЙ АНАЛИЗ
Параболой называется геометрическое место точек, одинаково удаленных от данной точки – фокуса и данной прямой – директрисы (рис. 7). Каноническое уравнение параболы имеет два вида: 1.
Рис. 7 2. Парабола Парабола Примеры 1. Составить геометрическое место точек, одинаково удаленных от точки Из условия 2. Написать уравнение параболы, проходящей через точку Каноническое уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид ПОЛУЧЕНИЕ ЭМПИРИЧЕСКИХ МОДЕЛЕЙ. РЕГРЕССИОННЫЙ АНАЛИЗ Регрессионным анализом называется метод построения модели на основе экспериментальных данных. Применение регрессионного анализа для обработки результатов наблюдений позволяет получить теоретическую зависимость (регрессию) переменных состояния системы от ее параметров и входных воздействий. Совокупность точек в пространстве, соответствующих экспериментальным данным (каждая из осей соответствует входному воздействию или параметру системы, одна из осей представляет собой отклик системы), называется корреляционным полем. Различают парную и множественную регрессию. Регрессия называется парной, если она представляет собой зависимость переменной y от единственной переменной x. Регрессия называется множественной, если получена зависимость переменной y от нескольких переменных x1, x2, …xn. Линейная регрессия ищется в виде линейной функции, нелинейная – в виде некоторой разновидности нелинейных функций. Регрессионный анализ состоит из двух основных этапов. 1 Определяется вид зависимости (общий вид функции) y = f(x), характер поведения которой близок к описанию поведения точек корреляционного поля. 2 Определяются параметры этой функции, при которых она наилучшим образом описывает (аппроксимирует) поведение точек корреляционного поля. Для нахождения теоретической линии регрессии (параметров выбранной функции) по данным экспериментальных замеров применяется метод наименьших квадратов. Суть его состоит в том, что отыскивается теоретическая линия регрессии у по х, такая, что сумма квадратов расстояний от этой линии до каждой экспериментальной точки с такими же х-координатами минимальна. То есть функция регрессии у по х строится таким образом, чтобы соблюдался принцип наименьших квадратов:
где j – порядковый номер точки в экспериментальном числовом ряду: yj – экспериментальное значение y для определенного значения аргумента хi; y'j – расчетное значение y при заданной величине аргумента хi в соответствии с их теоретической взаимосвязью (то есть полученное путем подстановки хi в уравнение теоретической зависимости). Для нахождения значений параметров функции, соответствующих принципу наименьших квадратов, находятся частные производные функции по этим параметрам и приравниваются к нулю. Решая полученную систему уравнений, получаем параметры функции, при которых она максимально приближена к точкам корреляционного поля.
|

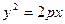 - парабола, симметричная относительно Ох;
- парабола, симметричная относительно Ох;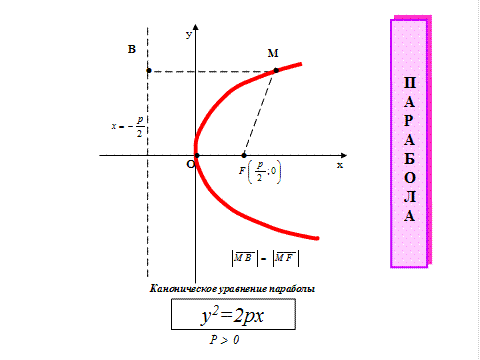
 - парабола, симметричная относительно Oу.
- парабола, симметричная относительно Oу.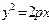 имеет фокус
имеет фокус  и директрису
и директрису 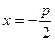 .
. и директрису
и директрису 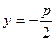 .
. и прямой
и прямой 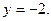
 , получаем
, получаем  , следовательно, это парабола, каноническое уравнение которой имеет вид
, следовательно, это парабола, каноническое уравнение которой имеет вид  или
или  .
.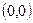 и
и 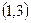 и симметричной относительно оси Ох.
и симметричной относительно оси Ох. , тогда искомое уравнение имеет вид
, тогда искомое уравнение имеет вид 
 .
. , (2.1)
, (2.1)


